Для оценки точности приближенного числа вводят понятие абсолютной погрешности.
Абсолютной погрешностью 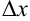 называют модуль разности между точным и приближенным значением величины, т.е.
называют модуль разности между точным и приближенным значением величины, т.е. 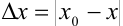 .
.
Абсолютная погрешность измеряется в тех же единицах, что и исходная величина.
Пример №45.1.
При измерении диаметра детали, точное значение которого равно 25,2 мм, было получено приближенное значение 25 мм. Оцените абсолютную погрешность проведенного измерения.
Решение:
Обозначим точное значение диаметра детали 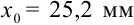 , а приближенное
, а приближенное 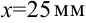 . Тогда абсолютную погрешность проведенного измерения найдем по формуле:
. Тогда абсолютную погрешность проведенного измерения найдем по формуле: 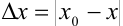 :
: 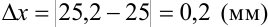 .
.
Ответ: 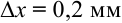 .
.
К сожалению, часто точное значение рассматриваемой величины является неизвестным. Поэтому для оценки диапазона, которому принадлежит точное значение числа, вводится понятие границы абсолютной погрешности.
Границей абсолютной погрешности приближения 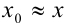 называют такое положительное число
называют такое положительное число 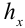 , больше которого абсолютная погрешность
, больше которого абсолютная погрешность 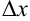 быть не может:
быть не может: 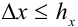 .
.
Если заданы приближенное число 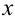 и граница абсолютной погрешности
и граница абсолютной погрешности 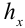 , то искомое точное значение числа
, то искомое точное значение числа  будет лежать внутри промежутка
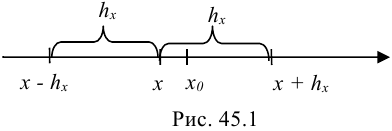
будет лежать внутри промежутка 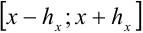 (рис. 45.1).
(рис. 45.1).
Для точного значения  удобна следующая запись:
удобна следующая запись: 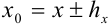 . Такое обозначение в практике часто используют при маркировке продукции. Например, на пакете молока объемом 1 литр может быть следующая запись:
. Такое обозначение в практике часто используют при маркировке продукции. Например, на пакете молока объемом 1 литр может быть следующая запись: 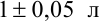 . Это означает, что содержимое купленного вами пакета может иметь объем от 0,95 л до 1,05 л, т.е. отличаться от номинала на 0,05 л.
. Это означает, что содержимое купленного вами пакета может иметь объем от 0,95 л до 1,05 л, т.е. отличаться от номинала на 0,05 л.
Граница абсолютной погрешности не определяется однозначно. На практике в качестве 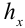 берется по возможности наименьшее число, которое удобно для вычислений и обеспечивает необходимую точность.
берется по возможности наименьшее число, которое удобно для вычислений и обеспечивает необходимую точность.
Существует правила нахождения границы абсолютной погрешности для чисел, взятых из таблиц, и для результатов измерений:
1. Граница абсолютной погрешности числа, взятого из таблицы, равна единице последнего разряда.
Например, табличное значение плотности чугуна 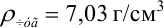 . Последний разряд данного числа — сотые. Следовательно, граница абсолютной погрешности
. Последний разряд данного числа — сотые. Следовательно, граница абсолютной погрешности 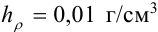 .
.
Табличное значение заряда электрона 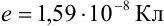 . Тогда граница абсолютной погрешности
. Тогда граница абсолютной погрешности 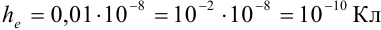 .
.
2. При измерениях граница абсолютной погрешности определяется по наименьшему делению прибора.
Так, при измерениях длины предмета 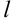 с помощью обычной ученической линейки граница абсолютной погрешности
с помощью обычной ученической линейки граница абсолютной погрешности 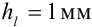 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Переход от алгебраической формы к тригонометрической и показательной. |
| Приближенные значения величин. |
| Относительная погрешность. |
| Запись приближенных чисел. Верные и значащие цифры. |
