Оглавление:

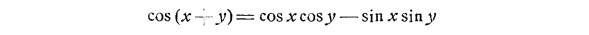




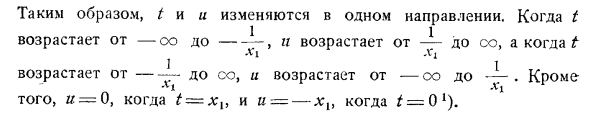




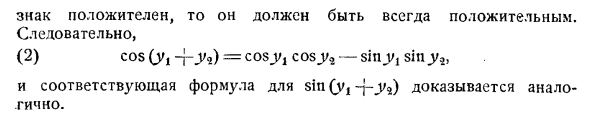
Аналитическая теория тригонометрических функций
- Теория анализа тригонометрических функций. мы Теперь вернемся к вопросу, кратко описанному в пункте 163. На протяжении всей книги читатель был знаком с элементами тригонометрии и считал, что он свободно использовал тригонометрические или «круговые» функции cosx, sin *, tg *, … в качестве примера. Основа тригонометрии не так проста, как кажется читателям, знакомым с ними поначалу, и обычное изложение теории основывается на ряде предположений, которые требуют тщательного анализа.
1 °. Геометрический метод. Наиболее естественный способ — максимально точно отслеживать отображение обычных учебников и переводить используемый в них геометрический язык на язык анализа. В пункте 163 мы обсудили этот вопрос и пришли к выводу, что возникла только одна серьезная проблема. Вы должны указать, что дуга окружности связана с конкретным числом, называемым его длиной, или что сектор окружности связан с конкретным числом, называемым его областью. Выполнение одного из этих требований достаточно для строгой демонстрации всей тригонометрии.
Существует, по крайней мере, четыре очевидных способа построения теории тригонометрического анализа. Людмила Фирмаль
Они обычно следуют первым двум путям и основаны на тригонометрии, основанной на понятии длины. Но гл. Конечно, второй метод был приоритетным, потому что VII включает строгий контроль области, а не длины. 2 °. Метод бесконечной линии. Второй метод, используемый во многих курсах анализа, заключается в определении тригонометрических функций с использованием экспоненциальных функций или бесконечных рядов, таких как 223. Определите cos x и sin x как уравнения (1) потому что x = 1-sin x = x— •••• Ряд Aegis отлично сходится для всех действительных значений x и может быть умножен на ряд в пункте 223. Поэтому излучайте формулу.
Это касательная формула сложения. Пока эта формула была доказана только при определенных ограничениях При условии, что значение переменной, т.е. если и если xr> 0 и- X-> + oo на левой стороне, x (<0 на правой стороне С ху х — * — оо и у-у? :. Таким образом, ограничения смягчены К тому, что V ,, y.2 и yt 2 должны находиться в интервале (-T * »t77) — Однако эти ограничения не являются необходимыми. Предел Y \ — ~ yy Интервал (-xv xr) не включает-. Примите это условие -vi Сломан, например, х1 О
| Биномиальный ряд | Функции комплексного переменного |
| Другой способ развития теории показательной и логарифмической функций | Действительные и комплексные криволинейные интегралы |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- И -и -x9 до xJy т увеличиваются и увеличиваются запад Изменение от 0 до co меняет знак и увеличивается с -oo на x. Итак, мы Ястреб кокс Гдл-Гдт-ГГ-1-Ж 1 + ° 2 J i + i * T J 1 + t * ‘z 0 От 0 до v = Jrftr «ГJГ-пр +. (‘ТХ7Г = K + arc tg О-о 0 так arc tgx = arc tg x {- {- arc tg l: r-r, Нет (6), ^ Oi + A) = ^ (Y1 + Y * — «) = = _ 4- _ тг ^ + тг ^ т l-xxxt 1-tg ^ tgjf, Точно так же это может быть выполнено, когда <0. Следовательно, (1) верно, если только yt находится в интервале. (-Y *. * 2 ‘
В этих случаях (1) Потерять смысл. 226. Из соотношения (1), пункты 225 и (4). 224 COS * (V 4 (l-tg.fttgjg * cos (v, i (i + tg ^ OCl + tg ^ — и = cos y-sin y, sinjf4) 2 cos Su, = ±: (cos Vj cos ^ 2-sin yx sin ^ 2).Установите ^ 2 = 0, чтобы определить знак. Уравнение выглядит так: ω $ <y, =; ± cosjy. Поэтому используйте положительный знак, когда _y2 = 0.
Наконец, так как каждая часть уравнения (1) является периодической функцией yy или yqt согласно (6), (1) есть ^ /, ^ 2, ^ /, «E должно быть нечетным кратным — ^ — n. Людмила Фирмаль
Выражение сохраняет положительный знак для всех кратных ux r, потому что обе стороны меняют знак при увеличении y на r. Кроме того, поскольку обе стороны уравнения являются непрерывными функциями yit, смена знака происходит только с обеих сторон, исчезает, то есть имеет значение 113 …, — ~ 2 ~ —Y1, 2 «~ —Yy» 2 77- * * » соответственно Уникальный на любом интервале длины м. Мы обнаружили, что для каждого такого интервала существует значение y0.
Если знак положительный, он всегда должен быть положительным. так (2) cos (y, ~ yy?) = Cos_Vj cos_y2-sinj /, sin ^ Vj, Соответствующее выражение для sin (y, -j-_y5) также доказано. cos (x-v) = cos xcosy — sin x sin y Дополнительные тригонометрические теоремы. Свойство периодичности имеет некоторые большие трудности. Из (1), если положительная функция cosjc меняет знак один раз в интервале (0.2) для малых значений x, это можно вывести, например, x = £.
Определения Число я по отношению = тогда $ в-я? Доказать, что = l, легко. cos tg = -1, sin 7r = 0. равенство cos (x g) = -cos l; sin (jc -f-em) = -sin l: Затем следуйте дополнительной формуле. Читатели найдут подробное объяснение теории, которая начинается с этих определений, в книге Уиттекера и Уотсона «Курс современного анализа», том 1, приложение А. Эта теория очень удовлетворительная, но более естественно рассматривать cos ^ r и sin 2: как функции комплексной переменной z, чем рассматривать только фактические переменные и функции. 3 °
Знак гениального определения с использованием бесконечного произведения. Третий способ — определить грех * по уравнению. Этот метод имеет много преимуществ, но, конечно, требует знания теории бесконечных произведений. 4 ° Определить обратную функцию, используя интеграл. Есть еще четвертый способ. Здесь следует отдать приоритет, так как мы почти повторили изложение логарифмической теории в первой части этой главы. Начните с определения arctgjt как уравнения X * J Tit Т + 7 * ‘ о
Эта формула однозначно определяет значение y%, соответствующее каждому действительному значению x. Поскольку подынтегральное выражение является четным, y является нечетной функцией от x. Кроме того, поскольку y непрерывен и строго возрастает, существует обратная функция jt = jc (y) согласно § 110, которая также непрерывна и строго возрастает. считать (2) x = x (y) = tgy. Определение r в уравнении (3) Тогда х (у) и 1 _ d dt 2 77 J 1 + ** ‘ о 1 ^ ^ 1 — 2 до <Y <2 * ‘
Теперь мы ставим (4) = WTU = yGFJ, Здесь подразумевается положительное значение маршрута. Таким образом, cos .y и sin ^ y определяются следующим образом: Для х- * оо, Итак, определите cos_v-> 0 и sin ^ y —► 1. cos y m: и 1. грех — ^ — м: равенством (5) cos y = 0, sin- = 1. Тогда cos y и sin ^ y определены для -i << y ^ r, а tg ^ y- определены для 1 ^ ^ 1 Наконец, определите \ gy, cos.y и sin для внешнего значения y («J t», используя 1 1 \ интервал-уравнение (6) tg (y + n) = tgy> cos (yf ~ ic) = -cos.y, sin (y -} — «) = -sin.y. Это определяет определение (-y15″ 2 » r) «(§d> / 5 3 . 1-Jr ”—T ~” ••••
Тогда функция tg ^ y определена для всех / 1 \ ^ y значение, исключая / c- | -) i (k является целым числом). Эти значения Определения не охватываются. Однако, если y имеет любое из этих значений слева или справа, tg ^ y будет ~} -oo или -oo. С другой стороны, cos .y и sin ^ определены и непрерывны для всех значений y. {1 \ Таким образом, если tgy- + oo для y ~ -I * 4 «-i ~ —O заменить на -f 0, знак изменится на противоположный. Чтобы убедиться, что уютно непрерывно с у = у » Это, во-первых, cos -i— = 0, по определению, во-вторых, но (4), 0 if cosy-y -> — 0, 3-й год -> — r — {- O cosy 0
(Хотя (4)) и в результате, однако (6) и уу ~ + Сначала мы определили acrtg ^ и tgy, затем через tgy мы определили уютные и греховные вещи. дуги sin a * и siny могут быть выбраны в качестве основных функций. В этом случае дуга x должна быть определена внутренним уравнением (-I, 1). 5 это Получено положительное корневое значение. синус-обратная функция; используйте g: -equality 1 г дф J. at Fra’1 2 о Уютные Tgy- отношения X cosy = y 1 «, tgy = p-r == — 4 (-1 <l: <1). Выбранный путь немного удобнее. 225.
Теперь мы сформулировали все необходимые определения, то есть определение, представленное уравнением с номером §224. Дальнейшее развитие теории зависит от формулы сложения. Прежде всего, (1 + **) (1 + /) = 0- * Y) * + (x + Y) \ Таким образом, dx , dy (I-j-ya) dx + (l + x *) dy 1 (1-ложь) «+ — _ (1-lg) </ (dg + y) — (l: -I-y) -, vy) dz (\ -Xy) * + (x + y) * 1 + где 1-х Это приводит к отношениям Дуга tg x arc igy = дуга tg z, Однако эти функции неоднозначны и должны рассматриваться более тщательно. Put — 1 _ L (X1 4- «) 14- ^ 1 \ o олово 1-я / л-т-.иил * * -1 — дги «я -} — xxt ‘ Вот так diz-1-hhh ‘(1-l-, “) * — (1-hkh)
Поэтому / и и меняем в одном направлении. Когда т увеличивается от -оо до ——, увеличивается от-до со, т j x, l-, Он растет от — до co и увеличивается от -oo до-. за исключением той Также, если t = x {=== 0, если f> 0, u = -xi).Теперь предположим, что x.g имеет значение, которое не включает точку u = -9, где интервал (-имеет значение -и t бесконечен. Для нее — и 0, хх должно быть больше, чем -.
В этих условиях X, A’j viih t увеличивается или уменьшается монотонно от 0 дт, — | -lg .. х = -ЖЖ. —При увеличении или уменьшении с хх до х>. с того времени (I- *; «) 2 Тогда у нас есть 1 xx -f c dt p du Дуга tg x = дуга tg = J ^ = J ^ = 0. *! -v «0 x *. xt -G я G ду G да «» J V + fl8 1 J «1 +» 2 • J О 0-Д «! = arc tg; c, -f- arc tg x>. Если я поставлю это сейчас y = arc tgx, y1 = arc tg *:, yy = arc tglg5 и GP trfv; y y — tgjr, + tgjf, (1) tg tVi -G-L) — * -! -s _tg yltgys ‘
