Задача №34.
Бифилярный маятник представляет собой систему, состоящую из тяжелого однородного стержня 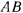 веса
веса  , подвешенного на двух параллельных нитях
, подвешенного на двух параллельных нитях 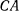 и
и 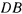 . Маятник переводится в новое положение
. Маятник переводится в новое положение 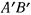 и в этом положении удерживается в равновесии горизонтальной парой сил с моментом
и в этом положении удерживается в равновесии горизонтальной парой сил с моментом  . Найти угол поворота стержня
. Найти угол поворота стержня 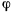 в положении равновесия системы, если
в положении равновесия системы, если 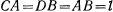 (рис. 7).
(рис. 7).
Решение:
Повернувшись на угол 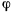 в горизонтальной плоскости, маятник поднимается вверх на некоторую высоту
в горизонтальной плоскости, маятник поднимается вверх на некоторую высоту 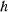 над своим первоначальным положением. Заметим, что в силу симметрии системы и действующих сил относительно вертикали, проходящей через центр тяжести стержня, центр тяжести маятника останется на этой вертикали и после перемещения, а сам стержень будет расположен в горизонтальной плоскости. Поэтому систему можно рассматривать как систему с одной степенью свободы. Возможное перемещение системы определяется изменением расстояния центра тяжести стержня
над своим первоначальным положением. Заметим, что в силу симметрии системы и действующих сил относительно вертикали, проходящей через центр тяжести стержня, центр тяжести маятника останется на этой вертикали и после перемещения, а сам стержень будет расположен в горизонтальной плоскости. Поэтому систему можно рассматривать как систему с одной степенью свободы. Возможное перемещение системы определяется изменением расстояния центра тяжести стержня 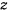 от линии
от линии 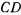 или изменением угла
или изменением угла 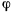 . Подсчитывая работу сил, действующих на систему, на этом возможном перемещении и приравнивая ее нулю, получим
. Подсчитывая работу сил, действующих на систему, на этом возможном перемещении и приравнивая ее нулю, получим
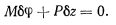
Обозначая через 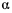 угол, который нить образует с вертикалью, будем иметь
угол, который нить образует с вертикалью, будем иметь
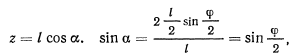
откуда
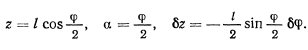
Подставляя значение 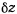 в уравнение равновесия, получим
в уравнение равновесия, получим
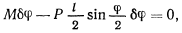
и тогда угол 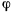 определится равенством
определится равенством
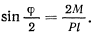
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
