Частные производные и дифференциалы
Дадим аргументу 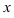 приращение
приращение 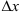 , аргументу
, аргументу 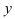 — приращение
— приращение 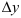 . Тогда функция
. Тогда функция 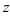 получит наращенное значение
получит наращенное значение 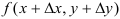 . Величина
. Величина 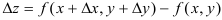 называется полным приращением функции в точке
называется полным приращением функции в точке 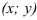 . Если задать только приращение аргумента
. Если задать только приращение аргумента 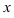 или только приращение аргумента
или только приращение аргумента 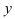 , то получим частные приращения функции
, то получим частные приращения функции 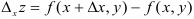 или
или 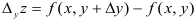 .
.
Заметим, что полное приращение функции, чаще всего, не равно сумме частных, т.е. 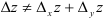 .
.
После определения частных приращений понятие частной производной вводится точно так же, как и для функции одного переменного: частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной независимой переменной при стремлении последнего к нулю.
Обозначения: 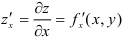 и аналогично — по
и аналогично — по 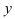 . Обычно используются все эти обозначения. Таким образом, для функции
. Обычно используются все эти обозначения. Таким образом, для функции 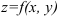 по определению:
по определению:
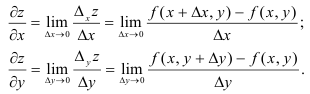
Геометрический смысл частных производных функции 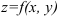 в точке
в точке 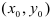 менее нагляден, чем для функции одного аргумента, но определяется точно так же. Если в данной точке поверхности провести две касательные в направлении осей
менее нагляден, чем для функции одного аргумента, но определяется точно так же. Если в данной точке поверхности провести две касательные в направлении осей 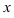 и
и 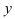 , то тангенсы углов наклона этих касательных (угловые коэффициенты касательных) по отношению к соответствующим осям и являются частными производными. Аналогичен и физический смысл: частная производная
, то тангенсы углов наклона этих касательных (угловые коэффициенты касательных) по отношению к соответствующим осям и являются частными производными. Аналогичен и физический смысл: частная производная 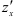 является скоростью изменения функции
является скоростью изменения функции 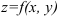 в данной точке по направлению оси
в данной точке по направлению оси 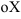 , a
, a 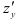 — по направлению оси
— по направлению оси 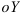 .
.
Все теоремы и свойства для производной первого порядка функции одной переменной, изложенные ранее в теме 7, без каких-либо изменений переносятся и на частные производные. Единственным существенным дополнением, вытекающим из определения частных производных, является то, что при дифференцировании по одному аргументу, второй, в этом процессе, считается постоянным числом.
В теме 7 дифференциал 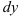 функции
функции 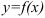 определялся как главная, линейная относительно
определялся как главная, линейная относительно 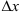 , часть приращения функции, равная произведению
, часть приращения функции, равная произведению 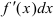 . Аналогично, для частных производных можно определить и частные дифференциалы
. Аналогично, для частных производных можно определить и частные дифференциалы 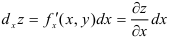 и
и 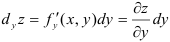 . Наконец, полным дифференциалом функции двух переменных
. Наконец, полным дифференциалом функции двух переменных 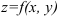 называется сумма частных дифференциалов, т.е.
называется сумма частных дифференциалов, т.е. 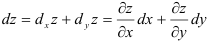 .
.
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Обратите внимание на эти страниц, возможно они вам будут полезны:
| Абсолютные экстремумы функции двух переменных |
| Градиент функции двух переменных |
| Формула трапеций |
| Теорема о среднем определенного интеграла |
