Числовые множества
Множество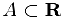 
называется ограниченным сверху (снизу), если существует действительное число 
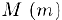такое, что для всех чисел 
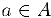выполняется неравенство
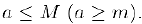
Числа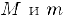 
называются, соответственно, мажорантой и минорантой множества А.
Ограниченное снизу и сверху множество, называется ограниченным.
Наименьшая из мажорант (наибольшая из минорант) называется верхней (нижней) гранью множества А. Верхняя грань обозначается через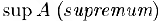 
. Для нижней грани используется обозначение 
.
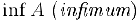В качестве примера рассмотрим множество
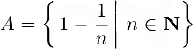
Здесь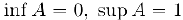 
.
Докажем теперь теорему о существовании граней множества.
Теорема 1. Ограниченное сверху (снизу) множество имеет. верхнюю (нижнюю) грань.
Доказательство. Предположим, для определенности, что множество А ограничено сверху. Обозначим через В множество его мажорант. Тогда для любых чисел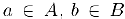 
выполняется неравенство 
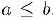. По свойству полноты множества действительных чисел (§1. свойство 9)) существует число-разделитель с такое, иго для всех 
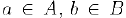имеет место неравенство
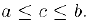
Таким образом, с одной стороны, число с: является мажорантой, а, с другой стороны, оно нс превосходит любой из мажорант и, следовательно,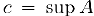 
. Аналогично доказывается существование нижней грани.
Рассмотрим систему вложенных отрезков
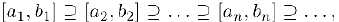
т. е.
Принцип вложенных отрезков. Любая система вложенных отрезков имеет непустое пересечение.
Доказательство. Пусть множества А и В состоят из левых и правых концов отрезков, соответственно. Так как для любых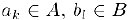 
справедливо неравенство 
,
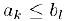то по свойству полноты множества действительных чисел найдется разделитель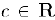 
. этих множеств и, следовательно, дня всех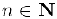 
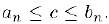
Таким образом, число с принадлежит всех отрезкам системы. Принцип доказан.
Множества можно сравнивать по количеству элементов, содержащихся в них. Конечные множества считаются равномощными, если они имеют одинаковое ’тело элементов. Если множество содержит бесконечное количество элементов, то можно попытаться сравнить его с другим бесконечным множеством простой структуры. например, с множеством натуральных чисел.
Бесконе’шое множество называется счетным, если его элементы можно пронумеровать, т. с. каждый элемент множества получает свой, отличный от других номер, выражающийся натуральным числом.
Примерами счетных множеств могут служить, например, множества целых и рациональных чисел. Целые числа можно пересчитать, расположив их в ряд:
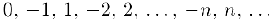
Для того, чтобы пронумеровать рациональные числа, расположим их в следующей бесконечной матрице:
В строках этой матрицы записаны все несократимые рациональные дроби с фиксированным знаменателем. Ясно, что каждому рациональному числу однозначно найдется место в этой матрице. Занумеруем теперь числа матрицы по диагоналям, на’шная с левого верхнего угла, т. е.
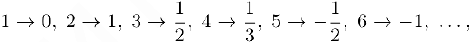
где запись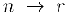 
означает, что рациональное число 
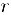получает номер 
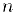. Таким образом, каждое рациональное число будет пронумеровано и, следовательно, множество 
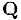счетно.
На этих примерах мы наблюдаем любопыппдй парадокс, который является особенностью бесконечных множеств: бесконечное множество может быть равномощно своей части, т. с. содержать столько же элементов, сколько их имеется в собственном подмножестве.
В заключение этого параграфа покажем что существуют множества, которые являются более мощными, чем счетные.
Теорема 2. Любой отрезок множества действительных чисел является несчетным множеством.
Доказательство. Предположим, наоборот, что отрезок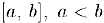 
является счетным множеством и пусть
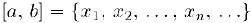
— пронумерованное множество чисел этого отрезка. Выберем внутри данного отрезка отрезок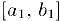 
, который нс содержит число 
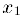, внутри отрезка 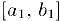найдется отрезок 
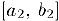. не содержащий число 
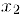, …, внутри отрезка 
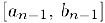возьмем отрезок 
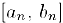, в котором не содержится число 
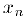, …. В результате мы получим систему вложенных отрезков
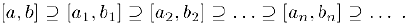
В соответствии с принципом вложенных отрезков, найдется число с, общее для всех отрезков. Пусть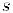 
— номер этого числа, т. е. 
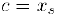и, следовательно, 
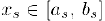. Полученное противоречие и доказывает утверждение теоремы.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
