Неравенство, в отличие от уравнения, вместо знака равенства содержит знаки неравенств 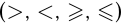 . Неравенства со знаками
. Неравенства со знаками 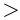 и
и 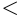 называются строгими, со знаками
называются строгими, со знаками 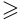 и
и 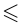 — нестрогими.
— нестрогими.
Два неравенства 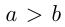 и
и 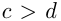 называются неравенствами одного знака, неравенства
называются неравенствами одного знака, неравенства 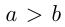 и
и 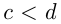 — неравенствами противоположных знаков. Вместо двух неравенств
— неравенствами противоположных знаков. Вместо двух неравенств 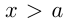 и
и 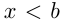 пишут
пишут 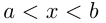 , это неравенство называется двойным.
, это неравенство называется двойным.
Свойства неравенств
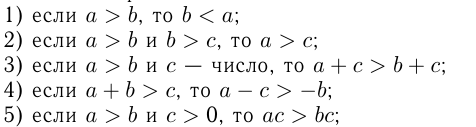
если 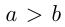 и
и 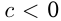 , то
, то 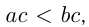 т.е. при умножении обеих частей неравенства на положительное число знак неравенства сохраняется, при умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный;
т.е. при умножении обеих частей неравенства на положительное число знак неравенства сохраняется, при умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный;
6) неравенства одного знака можно почленно складывать, например, если 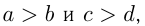 то
то 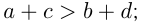
7) неравенства противоположных знаков можно почленно вычитать, ставя знак того неравенства, из которого производится вычитание, например, если 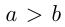 и
и 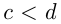 , то
, то 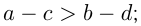
8) неравенства одного знака с положительными членами можно почленно умножать, например, если 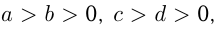 то
то 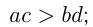
9) обе части неравенства с положительными членами можно возводить в натуральную степень, например, если 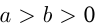 , то
, то 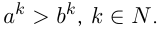
Решением неравенства считается такое множество значений переменной, при котором каждое число этого множества превращает исходное неравенство в верное числовое неравенство.
Линейным называется неравенство вида 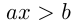 (или
(или 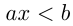 ;
;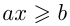 ;
;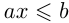 ), где
), где 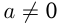 и
и 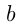 — числа.
— числа.
Решение линейного неравенства:
1) если 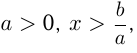 или
или 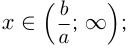
2) если 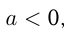 то
то 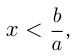 или
или 
Соответственно решаются и другие линейные неравенства.Здесь действует свойство 5.
Квадратичное неравенство — это неравенство вида: 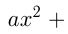
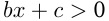
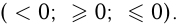
Если 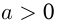 и
и 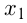 и
и 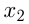 — корни уравнения
— корни уравнения 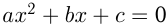 , то решением этого неравенства будут
, то решением этого неравенства будут 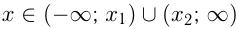 если
если 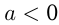 , то
, то 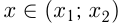 .
.
Другие квадратичные неравенства решаются аналогично. Например: 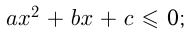
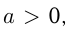
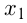 и
и 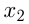 — корни уравнения
— корни уравнения 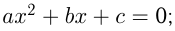 тогда решение неравенства:
тогда решение неравенства: 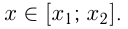
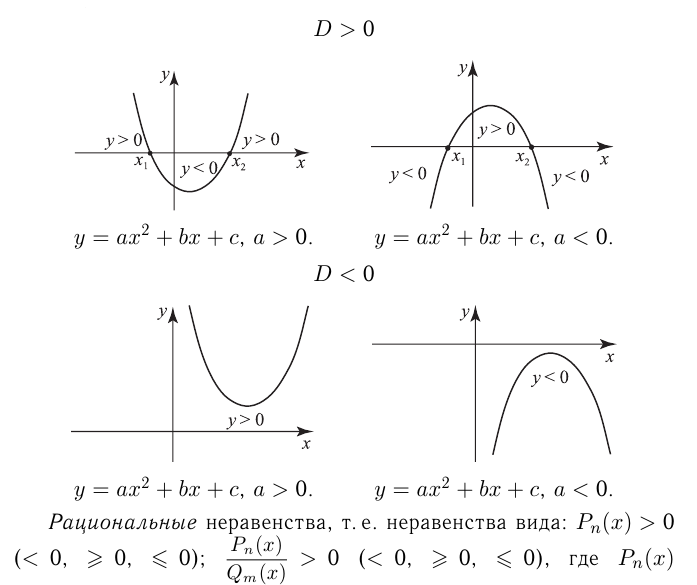
Если уравнение 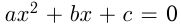 не имеет корней, то при
не имеет корней, то при 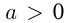 соответствующая парабола расположена над осью
соответствующая парабола расположена над осью 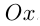 , и
, и 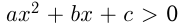 при всех
при всех 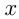 , т.е.
, т.е. 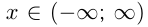 — решение неравенства
— решение неравенства 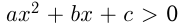 ; при
; при 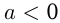 парабола находится под осью
парабола находится под осью 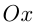 и
и 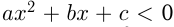 при всех
при всех 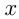 , т.е.
, т.е. 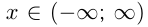 — решение неравенства
— решение неравенства 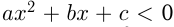 .Все, что было сказано, удобно проиллюстрировать с помощью графиков:
.Все, что было сказано, удобно проиллюстрировать с помощью графиков:
и 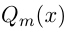 — многочлены степеней
— многочлены степеней 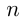 и
и 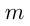 , обычно решаются методом интервалов. Отметим, что неравенство
, обычно решаются методом интервалов. Отметим, что неравенство 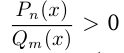 равносильно неравенству
равносильно неравенству 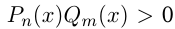 . Для того, чтобы решить неравенство
. Для того, чтобы решить неравенство 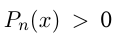 методом интервалов, нужно разложить многочлен
методом интервалов, нужно разложить многочлен 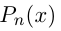 на множители:
на множители:
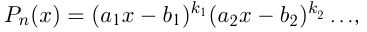
затем найти все нули многочлена, т. е. значения 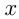 , которые обращают в
, которые обращают в 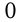 каждую скобку; отметить их на числовой оси и пользоваться таким правилом:
каждую скобку; отметить их на числовой оси и пользоваться таким правилом:
1) за крайней правой точкой всегда ставится 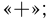
2) после следующей точки знак меняется на 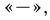 если степень соответствующей скобки нечетная; если степень четная — знак сохраняется;
если степень соответствующей скобки нечетная; если степень четная — знак сохраняется;
3) каждый раз при переходе через отмеченную точку знак меняется, если степень скобки, относящейся к этой точке, нечетная, и не меняется, если степень четная.
Квадратичные неравенства также можно решать методом интервалов, если разложить квадратный трехчлен на множители: 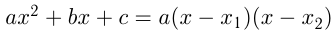 , где
, где 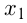 и
и 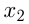 — корни уравнения
— корни уравнения 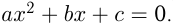
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение логарифмических уравнений |
| Решение тригонометрических уравнений |
| Решение задач на неравенства |
| Неравенства с радикалами задачи с решением |
