Оглавление:

























Дальнейшие сведения из теории рядов
- Подробная информация из теории ряда 11 ° 1. Основные характеристики серии. Теорема 1. Сходящаяся линия может быть сложена для каждого члена. Другими словами, + + (I) + A (2) тогда (Ax + M + (o, + A0 + (a. + A + … = A + A (3) Доказательство. „Bn и SH являются частичными суммами рядов (1), (2) и (3). Ля = *! + * • + ••• + I / 1 »Bn-b 1 + ••• $. = («I + * I> + … + <» — + * -> ■ тогда Sn = AH + Bn. Однако, в конце концов, n- + oo имеет Al- + A, Bn- + B и SH — *> A + B. Это эквивалентно уравнению (3). Теорема 2. Если все члены сходящегося ряда умножаются на одно и то же число, ряд остается сходящимся, а сумма умножается на это число. Доказательство. делает еи + эт + еи + … javA (I) Сформировать линию sah-j- sa% + sag + ••• (4) •) Предлагаемое дифференциальное уравнение является уравнением Эйлера.
Следовательно, y = Yx = Y1 + J (n: -1) может быть легко установлено. Требуемое разложение получается с использованием двоичного ряда. Рекомендуется найти его, используя метод неопределенных коэффициентов.После этого ряд (20) расходится. Доказательство. Неравенство (21) DL <al + 1 * так 0 <D1 <i * <a3 <… » Другими словами, n-й член в ряду: «Если I увеличивается, он удаляется от нуля. ♦) J. (G A1 esh b gt (1717-1783) — французский математик и механик. Очень привлекательно доказать, что ряд (20) сходится для всех п. Dd-н оп <B Однако это невозможно. На самом деле, гармонический ряд Будете ли вы N _LLJZ_L- «1 al-I- / H-1 ^ 1 ‘ И он будет расходиться!
Однако все н <0,9. Тогда ряд (20) сходится. Если то же самое верно <0,99 В * Такие, как. Это справедливо Лемма 2. ….. Умножая эти неравенства, <я ‘ ( Или то же самое 9p смысл То есть серия (20) является второстепенной + atq -f atf -f arf + … (23) Вверх + \
При положительном ряду (20) все n в / 1 + я Где q — константа, меньшая 1. 0 Людмила Фирмаль
Тем не менее, (23) является геометрической последовательностью с е в качестве знаменателя. С тех пор эта последовательность сошлась, а затем (первый Ряд сравнения) также сходится (20). Теорема (символ Даламбера) ограничивает положительный ряд (20) > Ish2Yi = P- + Co AP Если 1, ряд (20) расходится, если / <1, этот ряд сходится. Доказательство. Давайте начнем с 1. Большое отношение n приблизительно равно / таким образом, эти n вверх Встретить неравенство 1. (24) «Я Как только n больше m, это неравенство начинает выполняться.
Где m — фиксированное натуральное число. Тогда строка O / I + 1 + I | I + «+ arn + s + ••• (25) tio Лемма 1 должна быть разветвленной ). Но эта серия является остальной частью серии (20). Следовательно, ветвь (20). Здесь f <>. Поскольку отношение больших n почти равно /, для этих n выполняется неравенство Предположим, что это неравенство выполняется для η такого, что η> m. Где m — фиксированное положительное целое число. Далее лемма 2 сходится к ряду (25), и доказательство заканчивается так же, как и случай! *) Непосредственно к нашей серии (20) лемма! Эта лемма неприменима, поскольку предполагается, что неравенство верно для всех π, а (24) верно только для η> m.
- Пример. 1) Рассмотрим ряд, где ap = ~ 9 al +, = Я отсюда И один -2л 2 * Поэтому ряды будут сходиться. 2) Для номеров. и 2 г * н \ Pn Будете ли вы l «‘V1» «(i + — (l +1> l Таким образом, * n + 1 _ 3-й »_ 3 3 ^ (I-F- 1) л \ и «е ^ 1- (‘+ 4G Поэтому серия веток. 3) О цифрах 1 + T + T + T + — ™ Будете ли вы 1 1. л + 1 р 1_ L Этот случай не предписан теоремой, но вы можете видеть, что ряд (26) разветвляется без теоремы. 4) Подобные серии Также будет Но эта линия сходится.
Примеры 3) и 4) NT = \ l- »oo ap оп Здесь = л- с Вы можете видеть, что ряд (20) является как сходящимся, так и расходящимся. 5) Просмотрите серию рн + я = Поэтому я + 1 л + 1 В результате ряд сходится. Поскольку общий член ряда сходимости имеет тенденцию быть нулевым, И мы получили новое доказательство леммы из n ° 3§1. № 4. Существенный признак конвергенции. Отпусти меня +++ (27) И некоторые заданные функции f (*) Для всего натурального п получается (28) Пн) = Вверх.
Далее, f (x) называется функцией генерации серии (27). Например, функция ~ представляет собой гармонический ряд 1 + + Y + -3 + ••• (29) 1 Сходятся или расходятся одновременно. Доказательство.
Теорема (критерий интегрирования сходимости) Ряд (27) имеет непрерывную и положительную убывающую генераторную функцию f (x). Тогда серия и неуместная интеграция +00 \ f (x) dx Людмила Фирмаль
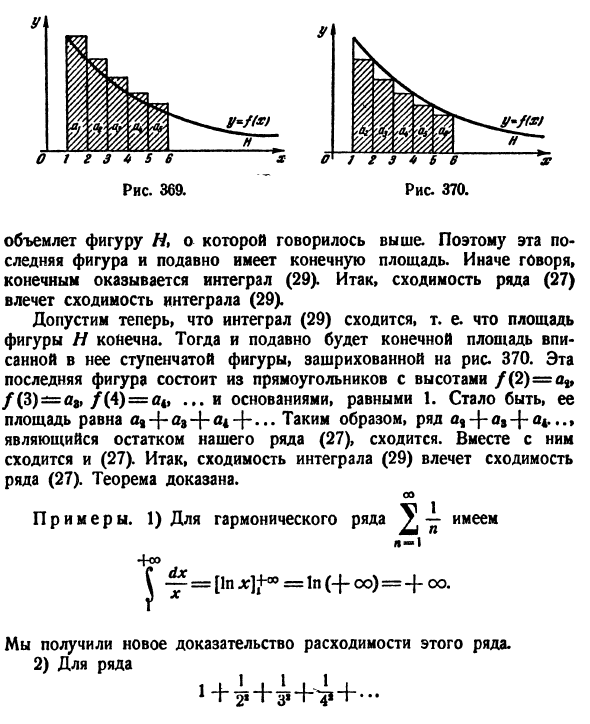
Ряд (27) положителен ), поэтому сумма, конечно, конечна или бесконечна. Аналогично, всегда есть интеграл (29), который является интегралом положительной функции, но он может быть бесконечным. Этот интеграл является областью фигуры H, ограниченной осью Ox, ограниченной слева линией y = f (x) сверху, то есть графиком функции / () линией x = \ Не ограничивается •) = / (n)> 0. Справа (Рисунок 369). Легко понять, что нарисовано на рисунке. Высота прямоугольника 369 равна / (1) = H |, / (2) = o * / (3) = a & D4) = a4, … поэтому основание всех этих прямоугольников равно 1 Потому что площадь постоянно равна ах, а%, а2, … Предположим теперь, что ряд (27) сходится, то есть сумма -f-Of -f-a, -f -… конечна.
Тогда есть окончательная сумма вышеупомянутых прямоугольных областей. Другими словами, последняя область — это лестничная диаграмма, составленная из этих прямоугольников. Но эта лестничная фигура ясна прямо из фигуры Рисунок 369. Включает рисунок H, как указано выше. Следовательно, эта последняя фигура также имеет конечную площадь. Это означает, что интеграл (29) конечен.
Следовательно, сходимость ряда (27) означает сходимость интеграла (29). Теперь предположим, что интеграл (29) сходится, то есть площадь фигуры А конечна. Кроме того, конечная площадь гравированной лестницы с затененной фигурой еще больше. 370. Последняя фигура состоит из прямоугольника с высотой / (2) = <μ, / (3) ^ = n „/ (4) = π4, …, нижняя часть 1. Площадь ++, поэтому ряд a% -} — ar — {- a4 …, Остальная часть ряда (27) сходится.
В то же время (27) сходится. Следовательно, сходимость интеграла (29) означает сходимость ряда (27). Теорема доказана. и Пример. 1) О серии гармоник ^ -Мы я-1 = [In x} + ”= In (+ oo) = + oo. Мы получили новые доказательства расхождения этой серии. 2) О цифрах 1 + 2 «+ h» + 4i + — » Рисунок 370
Генерация / (*) = p и атрибут интеграции YS-Н-г — «- Другими словами, ряд будет сходиться. Интересно, что на оба этих сериала Далленвейл не дал ответа. 3) О цифрах 1,2.3.4. час Т.е. 1 ‘3 * 2 * -I’ 3 * 3 * -1 • 3,4 ‘- 1’ Функция генерации: / (■ *) = j. с того времени Затем серия ветвится. Опять же, символ Далленвале не применяется. № 5 Альтернативные линии. Определение Когда два соседних элемента имеют разные знаки, ряд называется чередующимся *)>. До сих пор l-й член серии был указан как. В этом разделе мы оставим это и покажем абсолютное значение l, а не сам l-й член. Затем, для ясности, предположим, что первый член чередующегося ряда положителен, и запишите его в виде <* i-a * -} — a, -a4 -f —… (30) Теорема Лейбница.
Если модуль r-го члена чередующегося ряда уменьшается с ростом n, он стремится к нулю, после чего ряд сходится. Доказательство. Рассмотрим ряд (30), предполагая следующее: sh shop = 0. (30a) I- и Пусть Sn будет l-й частичной суммой ряда. тогда Si = (at-aj + (at-a4), $ • = 0 * 1-а,) + (а3-фли) + (а, -ин *), 5, = (aj-a *) — Ха, -a ^ + fa-a4) -} — (a7-a% \ *) Ходить попеременно иногда. Каждое различие, записанное в скобках, положительно по первому условию (30a). так S1 0, так S «n <a f. Следовательно, переменная S ^ — это количество, ограниченное выше. Существуют конечные ограничения двух свойств этой переменной. p- + sa Указывает, что такое же ограничение имеет тенденцию происходить ^ -Si n + — + S — \ — 0 = S
Если An и Sn являются частичными суммами рядов (1) и (4), то есть И я = <* t ++. •• + ay ”Sn = sah + ca% -f ••• + n * n>, затем Sn = cAn. sah-f- -f- sah -J -… = s A. (5) (6) Теорема 3. Члены ряда сходимости стремятся к нулю при увеличении числа. Другими словами, линия Converge Доказательство. Aya и A обозначают n-ю частичную сумму и сумму ряда соответственно (5). тогда K = <* i + -J -… + a ^ x -f an Как хорошо Ap_i = ax + a, … + fl / i-i » Откуда Но в, есть Ap A и A. Следовательно, ap A-A = O, Докажите (6). Замечания.
Теорема 3 означает, что соотношение (6) является необходимым условием сходимости ряда (5). Гармоническая серия И ветвь. Так как эта линия 1 Это значит Следовательно, независимо от того, является ли индекс n четным или нечетным, Теорема доказана. Пример. ряд 1 4-1-1 4-1- Converge. Мы уже упоминали, что при n ° 6§1 сумма равна In2. Замечания. 1) Условие уменьшения модуля общего члена не может быть отброшено. На самом деле, рассмотрим чередующиеся серии ! _ ± _L ± L_LJ \ 1 в г 9 в »га и 10 ”2 10” 1 3 10 ”
Но у него много поворотных моментов: сумма членов, стоящих нечетно Поскольку место бесконечно, а сумма геометрической прогрессии (знаменатель 0.1) конечна, сумма членов, стоящих в четных местах, конечна. 2) Было обнаружено, что Sqn приблизился к S и увеличился. Наоборот, увеличение n уменьшает его. конечно Sg = at- (Oa-Oj), Sb = ai — (<h — fa- И каждое различие, написанное в скобках, является положительным, Si ^ s …
Поэтому, если ряд (30) удовлетворяет условиям теоремы Лейбница, сумма S% n является приближением общей суммы 5 пропущенных, а сумма £ ad + 1 является чрезмерной. 3) Одна и та же идея может быть выражена по-разному. Обратите внимание, что S, = ax и = g, -a * 0. Следовательно, неравенство дать 0 <£ <> „ То есть сумма ряда, удовлетворяющего теореме Лейбница, имеет тот же знак, что и первый член ряда, а ее абсолютное значение меньше.
Обратите внимание, что остальная часть ряда, которая удовлетворяет условиям самой теоремы Лейбница, удовлетворяет условиям этой теоремы, поэтому только что приведенное объяснение применимо к ней. Сумма остатка после n-го слагаемого равна /? Для L уравнение S = Sm + Rm Это приводит к выводу. Ошибки, допущенные путем разбивки набора значений, удовлетворяющих теореме Лейбница, имеют тот же знак, что и первый отброшенный член, а его абсолютное значение меньше.
Это свойство рядов, которые удовлетворяют условиям теоремы Лейбница, делает такой ряд очень полезным для численных расчетов, поскольку он может оценить ошибку, вызванную заменой суммы ряда на его частичную сумму. Пример. делает o 1 1, 1 1,1 1-Т «31 4 * ‘5 *» » Замена £ на сумму экспортированных условий приведет к отрицательной ошибке. ^ = 4bq <0’00003-
№ 6. Абсолютная конвергенция. Общие симптомы Даламбера. Теперь рассмотрим серию, членами которой может быть любое количество символов. В отличие от предыдущего n °, символ снова указывает p-го члена ряда, а не только его абсолютное значение. Теорема. Рассмотрим одновременно с числами ++ (31) Многие модули этого члена в «1 + | в || + | v.1 + | v4 | + … (32) Когда ряд (32) сходится, (31) также сходится. Доказательство. Отпустить + * + * + — (33) Серия состоит из всех положительных членов серии (31) (34) Состоит из модуля всех отрицательных членов ряда (31) *). Ряды (33) и (34) вложены в ряды положительной сходимости (32) и сходятся с теоремой n ° 2. Пусть B и C — сумма, Bp и Cx Их личное количество. Рассмотрим частную сумму = + + + Линия (31).
Среди написанных здесь терминов, если p = p (n) положительно и q = q (n) отрицательно, очевидно, An = Br-Shah. Для n- + oo, **) и p- + oo, q oo. Но потом bp + c, cq- + c Следовательно, существование An- + B-C. Конечный предел lim An доказывает теорему. Замечания. Эта теорема необратима. Он не состоит из последовательной сходимости, сходящейся к (31). Например, числа 1 _ ± + ± — ± 4- ± — •).
Например, если серия (31) имеет вид: , 1__L L ± J ! _ | ! я ! . L + T 7 ’45 63 147 200 1000 t007 ^ » ‘Тогда серии (32), (33) и (34) будут иметь вид 1 D. 1 4- 1 4- 1 4- 1 i ! _ я ! L 1 L i ‘2’ T 45 63’147 ‘200 1000 1007 1 + 45 + 63 + 200 + T000 + «» ± J_ ± J ! L _ ± _ 2 ^ 7147 ‘1007 ••) Рассмотрим (31), где есть положительное бесконечное множество и отрицательное бесконечное множество. В остальном все понятно. По теореме Лейбница сходятся и ряды модулей ее членов являются гармоническими рядами ^ T + Y + T + ¥ + Как мы знаем, это ветвится. Вы можете видеть, что сходимость ряда (32) означает больше, чем сходимость ряда (31).
Поэтому удобно давать Серия определений (31) называется абсолютно, если сходится не только данный ряд (31), но и ряд модулей (32) этого члена Конвергенция. Если ряд (31) сам сходится и (32) расходится, то (31) называется неабсолютным рядом сходимости. Теорема 2. [Общий стандарт Даланвала. ) ++ (31) Как ограничения <* пи ау lim «- ♦ 00 Далее, в случае ряда (31) он полностью сходится, а в случае 1 И ветвь. Доказательство. Во-первых, 1. Сравните с серией модулей от участников серии (31). М + 1 ** 1 + | + … (32) Эта серия положительна, и атрибут d’Alembert может быть применен.
Но ведь Оя + 1 Iip + 1I \ ° n \ Следовательно, (32) сходится. То есть ряд (31) полностью сходится. Давайте рассмотрим случай 1. После этого нельзя сделать вывод о работе ряда (31), поэтому ничто не может быть достигнуто путем привлечения ряда (32). Однако легко доказать теорему напрямую, не используя ряд (32). С какого Овцы -1 е> б Если η достаточно велико, n ^ r *> 1, то есть \ ap \ ^ l l I- Как только это неравенство начинает происходить, абсолютное значение члена в ряду (31) начинает увеличиваться. Другими словами, член ряда (31) удаляется от нуля. Это указывает на то, что условие (0), необходимое для сходимости ряда, не выполняется и ряд расходится.
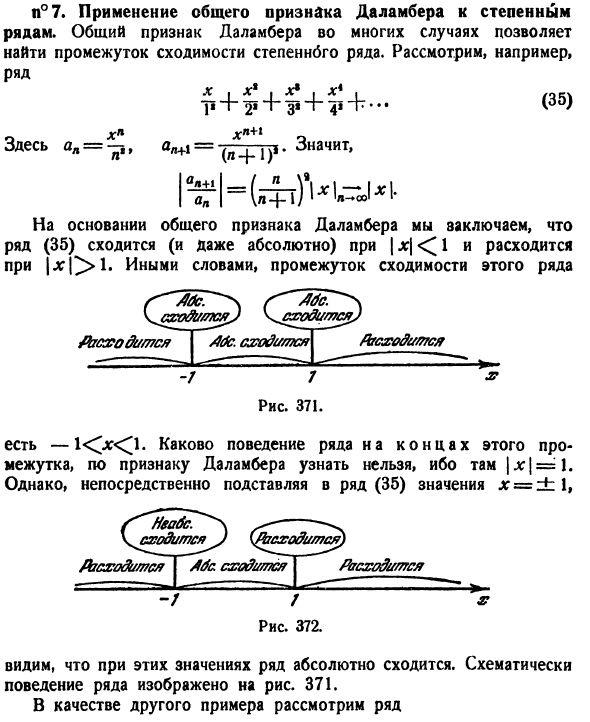
№ 7 Применение общего свойства Даламбера к степенным рядам. Во многих случаях для нахождения интервалов сходимости степенных рядов можно использовать общий критерий Даламбера. Например, рассмотрим серию Wi + 1 l Значение «L + 1 = лошадиная сила Где ау = <«+ O1 ^ hln-rrlVirj-i. Исходя из общего критерия Даламбера, мы заключаем, что ряд (35) сходится (и даже абсолютен) к |.
Расхождение x \ <^ 1 и другими словами интервал сходимости этого ряда «» «W ^ СХО & / 07СЯ ^ JbCXodt / тСЯ -1 <AG <1. Согласно Даламбе, каково поведение ряда в конце этого интервала? \ x \ == \ и не может быть распознан. Однако, если значение ряда (35) непосредственно присвоено Jt = dbl, Nyubusu. Converge 7СХО01 // 77С / П / B сходится 44s сходится и расходится Y г х Рисунок 372. С этими значениями вы можете видеть, что ряд полностью сходится.
Схематично работа серии показана на рисунке. 371. В качестве другого примера рассмотрим серию и Интервал сходимости такой же: — \ где x = \ Ряд (36) является расходящимся гармоническим рядом и сходится по теореме Лейбница, когда x = -1. Поэтому его действия имеют символы, показанные на рисунке. 372. Рассмотрим другую серию TT + 21+ 3I + — » здесь ‘/ 1 + 1 (36) т +? + т + т + — здесь , 1 * 1 ‘rt + l о И ряд будет сходиться для любого X *. «Интерес»: численные примеры и (37) 2 р \ х * Здесь для х ^ 0 Я (38) Поэтому ряд (37) расходится для всех x, кроме следующего. = Вернуться к двоичной серии Занимался §8§1.
Эта серия, как говорили, имела разрыв сходимости. Я смог доказать это. Конечно, серия (38) Далее вы можете видеть, что условие (6) недостаточно для сходимости ряда (5). Другими словами, нарушение этого условия гарантирует расхождение ряда, но его реализация не гарантирует конвергенцию. Пусть m натуральное число. ряд m An = («1 + + •. + Am) + OWi + т.е. [n = m — \ — (n-m) \ An = At + A * _t. (8) Предположим, что ряд (7) сходится к полному Rm. oo, n-m- + co (m фиксировано в конце концов!)
Сравнивая эту связь с уравнением (8), Ap Asch ~ b ^ t » То есть ряд (b) сходится к общему Am + Rm. Следовательно, сходимость остальных рядов означает сходимость самого ряда. Точно так же противоположное утверждение доказывается на основе того же уравнения (8). В середине, в случае сходимости рядов (5) и (7), было доказано, что их сумма A и Rm связаны следующим соотношением: ^ = -f- rfrr Это соотношение можно описать в более наглядной форме. от т 2 «» =! > «+ 2 л — 1/1 = 1 н = м-фл % положительная линия.
Признаки сравнения. Определение линии + «8 + — (5) Если все участники позитивны, это называется позитивом. Эта серия имеет большой палец Поскольку оно увеличивается с ростом n, неизбежно существует предел. Тренажерный зал (9) п-к Кроме того, предел (9) конечен, только если сумма Sn ограничена выше, то есть если существует постоянная K> такая, что все η известны S „<K. Это правда Теорема. Положительные линии всегда имеют сумму (конечную или равную + оо).
Сходятся, только если частичная сумма ограничена выше. Определение с учетом двух положительных линий + + (U) * + * + 00 Если все n присутствуют (12) Они говорят, что серия (11) является большинством по сравнению с серией (10), а серия (10) — немногим по отношению к (11). Другими словами, каждый член серии minorino меньше (точнее, не больше), чем соответствующий (то есть имеющий такое же число) член основной серии. Теорема 2. (Первый признак сравнения.) Сходимость младшего ряда следует за сходимостью основного ряда. Доказательство. Ряд (11) является большинством (10). Put At = ej + aa + …- {-a „, D” — + + С (12) АЯ ^ ВЯ. (13)
Предположим, что ряд (11) сходится. Тогда частичная сумма ограничена вершиной. То есть существует константа / C для каждого η. ва <к. Отсюда и (13) все n существуют, AY <K, И ряд (10) сходится.Доказанные теоремы также могут быть изложены в этой (эквивалентной) форме. Незначительное серийное расхождение означает существенное расхождение серии. Само собой разумеется, что основной ряд различий делает невозможным заключение поведения.
Пример. На n ° 2§1 серия _L + JL + JL + 1.2 ‘2.3’ 3.4 ”сходимости, но ясно, что эта серия важна для серии O4) Поэтому ряд (14) также сходится. Эта строка является остальной частью линии. -r ++! «+ •••» (15) Очень похоже на гармоники. Однако, в отличие от гармоник, ряд (15) сходится [потому что остальные (14) сходятся]. Теорема 3. (второй критерий сравнения) Дань двух положительных рядов ++ + (16) ++ (17) Когда существует конечный ненулевой предел для отношения одинакового количества членов в рядах (16) и (17) / = lim af (0
Эти линии затем сходятся или расходятся одновременно. Доказательство. Предположим, что ряд (17) сходится. делает Соотношение r5 стремится к пределу / «Я Достаточно большое значение n миллиард Так что это неравенство скоро станет реальностью Где m — фиксированное натуральное число. тогда n> mt, т.е. η = m — \ — \, m — \ — 2, m — \ — b, … Это серия +++. (18) небольшое количество + Lbm ¥ i — {-… (19) Последняя строка сходится. Фактически, это получается умножением всех членов ряда на L ^ m + i + -f- bm + s -f- .. Сходятся как остальные ряды сходимости (17).
Но тогда, как известно, сходились (19). Согласно первому признаку сравнения сходимость ряда (19) означает сходимость ряда (18). И это остальная часть серии (16). Следовательно, (16) также сходится. Следовательно, сходимость рядов (16) означает сходимость рядов (16). Поскольку эти ряды равны, противоположное предложение также верно и завершает доказательство
.Предполагая, что заранее al и bn (n-> oo) бесконечны (в противном случае все ясно: ряд, в котором член не становится равным нулю при увеличении расходимости числа), теорема Если члены двух положительных рядов an и bn бесконечно малы одного порядка, эти ряды сходятся или расходятся одновременно. Пример. ряд sinrc-f-sinsin JL-j-sin Расхождение sfa ~ lim -: — = ic. n- * co ± N В заключение докажем одну теорему, которую мы будем использовать позже.
Теорема 4. Дайте положительный ряд, который сходится (для вложенных рядов). (19а) Пусть nt <n, <i, <… — возрастающая последовательность натуральных чисел. Тогда строка <* L1 + ON, + ap, + … (196) Чтобы сходиться *). Доказательство. Sa и S * являются частичными суммами рядов (19a) и (196) соответственно. = OSH + OSH + ASH + … + 0P / » Все члены общего числа являются частью общего Sn / т. Кроме того, итоги могут включать такие термины, но не итого S *. с того времени •) Естественно назвать последовательность (196) «встроенной» в последовательность (19a), например последовательность y + — {4 + 2l + 2S + -. * Встроенный * Гармонический ряд 1 + ~ 2 +
Если ряд (19a) является положительным, все упомянутые «дополнительные» вещи (то есть те, которые находятся в общем Snft, но не в общем Sk), являются положительными. Но линия (19а) сходится. Следовательно, все частичные суммы меньше 1 и остаются неизменными. Sn <A. В частности, S „k <A. S ~ k <A. Поэтому частичная сумма положительных рядов (196) ограничена выше, и этот ряд сходится. № 3. Оба показателя сравнения, рассмотренные при n ° 2, имеют один и тот же недостаток: для изучения сходимости положительного ряда необходимо выбрать другой ряд для сравнения и его поведение (относительно сходимости) ) Известно.
Не существует общих правил поиска этой новой серии. Все зависит от изобретательности исследователя и запаса известных ему рядов сходимости и ветвления. Критерий сходимости положительных рядов в этом разделе, принадлежащий Даламберу *), не имеет этого недостатка. Этот символ не требует новой серии, кроме интересующей вас серии, но вам необходимо выполнить некоторые операции над самой указанной серией. Конечно, эта функция не является универсальной, но она часто решает проблему сходимости или расходимости рядов. Лемма / ♦ Дайте положительный ряд. <20) 01 + + a * + Когда найдены все н После этого ряд (20) расходится.
Смотрите также:
| Тройной интеграл | Координаты на плоскости |
| Криволинейные интегралы | Определение и геометрический смысл |
