Оглавление:
Делимость целых чисел
а) Множество натуральных чисел обозначают буквой 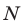 , а множество целых чисел — буквой
, а множество целых чисел — буквой 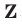 . Если
. Если 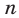 — натуральное число, то пишут
— натуральное число, то пишут 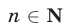 , а если
, а если 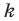 — целое число, то пишут
— целое число, то пишут 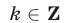 .
.
Натуральное число 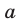 записывают так:
записывают так:
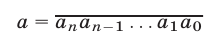
или в виде суммы
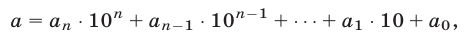
где 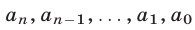 — цифры соответствующих разрядов.
— цифры соответствующих разрядов.
б) Если 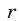 — остаток от деления натурального числа
— остаток от деления натурального числа 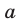 на натуральное число
на натуральное число 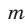 , то
, то
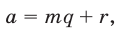
где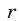 может принимать одно из значений
может принимать одно из значений 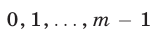 ;
; 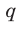 — целое неотрицательное число.
— целое неотрицательное число.
В том случае, когда 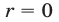 , говорят, что
, говорят, что 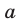 делится на
делится на 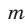 .
.
в) Если 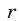 — остаток от деления натурального числа
— остаток от деления натурального числа 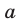 на натуральное число
на натуральное число 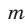 , то:
, то:
— остаток от деления на 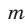 числа
числа 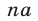 , где
, где 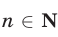 , равен остатку от деления на
, равен остатку от деления на 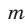 числа
числа 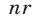 ;
;
— остаток от деления на 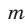 числа
числа 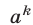 , где
, где 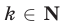 , равен остатку от деления на
, равен остатку от деления на 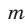 числа
числа 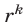 .
.
г) Если 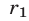 и
и 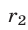 — остатки от деления на натуральное число
— остатки от деления на натуральное число 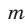 натуральных чисел
натуральных чисел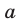 и
и 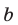 соответственно, то остатки от деления на
соответственно, то остатки от деления на 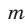 чисел
чисел 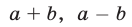 и
и 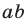 совпадают с остатками от деления на
совпадают с остатками от деления на 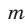 чисел
чисел 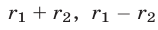 и
и 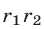 соответственно.
соответственно.
д) Натуральное число делится на 4 тогда и только тогда, когда двузначное число, полученное из данного отбрасыванием всех цифр, кроме двух последних, делится на 4.
е) Натуральное число делится на 3 (на 9) тогда и только тогда, когда сумма его цифр делится на 3 (на 9).
Пример №3.
Доказать, что число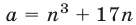 делится на 6 при любом натуральном числе
делится на 6 при любом натуральном числе 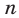 .
.
Доказательство. Эту задачу можно решить, применив метод математической индукции. Приведем другой способ решения. Заметим, что натуральное число делится на 6 тогда и только тогда, когда на 6 делится число 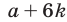 , где
, где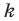 — целое число. В частности, число
— целое число. В частности, число 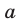 делится на 6, если число
делится на 6, если число 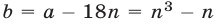 делится на 6. Но
делится на 6. Но 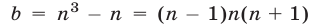 — произведение трех последовательных натуральных чисел, из которых одно делится на 3 и по крайней мере одно делится на 2. Поэтому число
— произведение трех последовательных натуральных чисел, из которых одно делится на 3 и по крайней мере одно делится на 2. Поэтому число 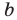 делится на 6, откуда следует, что число
делится на 6, откуда следует, что число 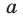 также делится на 6.
также делится на 6.
Пример №4.
Найти последнюю цифру числа 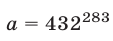 .
.
Решение:
Последняя цифра у числа 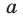 такая же, как и у числа
такая же, как и у числа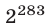 . Выпишем последовательные степени двойки:
. Выпишем последовательные степени двойки:
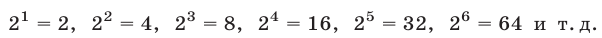
Отсюда следует, что последние цифры этих чисел повторяются через 4. Поэтому последняя цифра у числа 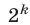 такая же, как у числа
такая же, как у числа 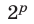 , где
, где 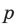 — одно из чисел
— одно из чисел 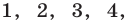 а разность
а разность  кратна четырем. Так как
кратна четырем. Так как 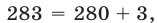 где 280 делится на 4, то последняя цифра числа
где 280 делится на 4, то последняя цифра числа 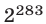 — восьмерка
— восьмерка 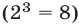 .
.
Замечание. Если рассматривать последовательные натуральные степени числа 3 (или числа 7), то можно заметить, что последние цифры получаемых чисел повторяются через 4. Поэтому последняя цифра у числа 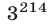 такая же, как у числа
такая же, как у числа 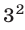 , т.е. девятка, так как
, т.е. девятка, так как 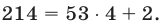
Аналогично, последняя цифра числа 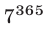 — семерка, так как
— семерка, так как 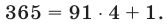
Пример №5.
Доказать, что число 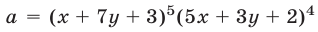 делится на
делится на 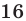 при любых целых
при любых целых 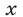 и
и 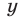 .
.
Доказательство. Если числа 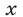 и
и 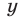 — оба четные или оба нечетные, то
— оба четные или оба нечетные, то 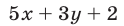 — четное число, и поэтому
— четное число, и поэтому 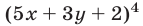 делится на
делится на 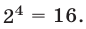 Если же одно из чисел
Если же одно из чисел 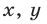 — четное, а другое — нечетное, то
— четное, а другое — нечетное, то 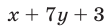 — четное число и поэтому
— четное число и поэтому 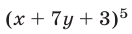 делится на
делится на 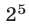 и, значит, делится на
и, значит, делится на 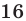 .
.
Пример №6.
Найти остаток от деления числа 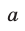 на
на 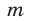 , если:
, если:
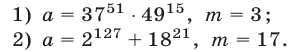
Решение:
1) Заметим, что если натуральное число 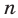 не делится на
не делится на 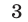 , т. е.
, т. е. 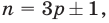 где
где 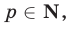 то
то 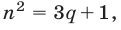 где
где 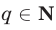 . Поэтому остаток от деления на
. Поэтому остаток от деления на 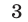 числа
числа 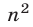 равен
равен 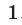 , если
, если 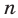 не делится на
не делится на 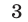 . Числа
. Числа 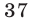 и
и 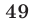 не делятся на
не делятся на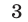 и, следовательно, остаток от деления на
и, следовательно, остаток от деления на 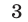 каждого из чисел
каждого из чисел 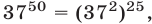
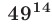 равен
равен 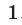 , а остаток от деления на
, а остаток от деления на 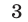 числа
числа 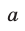 совпадает с остатком от деления на три числа
совпадает с остатком от деления на три числа 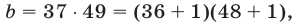 т.е. равен
т.е. равен 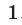 .
.
2) Так как 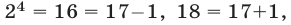 а
а 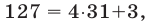 то остаток от деления на
то остаток от деления на 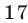 числа
числа 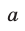 совпадает с остатком от деления на
совпадает с остатком от деления на 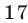 числа
числа 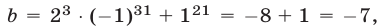 т. е. равен
т. е. равен 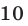 , поскольку
, поскольку 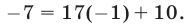
Ответ. 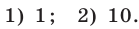
Пример №7.
Доказать, что натуральное число
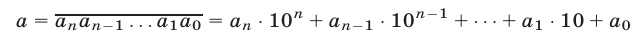
делится на  тогда и только тогда, когда на
тогда и только тогда, когда на  делится сумма
делится сумма
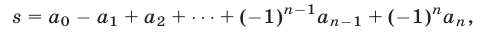
т.е. сумма цифр этого числа, взятых с чередующимися знаками.
Доказательство. Остаток от деления на 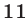 чисел
чисел 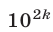 , где
, где 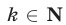 , равен
, равен 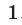 , так как
, так как 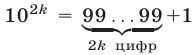 , а остаток от деления на
, а остаток от деления на 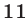 чисел
чисел 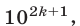 где
где 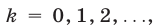 равен
равен 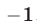 , так как
, так как 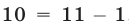 ,
, 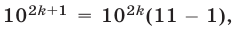 а остаток от деления на
а остаток от деления на 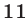 числа
числа 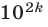 равен
равен 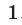 .
.
Итак, остаток от деления на 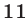 числа
числа 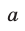 равен
равен 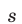 .
.
Пример №8.
Доказать, что если число 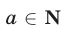 не делится на
не делится на 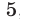 , то число
, то число 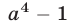 делится на
делится на 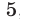 .
.
Доказательство. Пусть 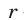 — остаток от деления
— остаток от деления 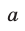 на
на 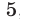 . Так как
. Так как 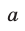 не делится на
не делится на 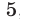 , то
, то 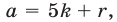 где
где 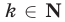 ,
, 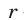 — одно из чисел 1, 2, 3, 4. Из равенства
— одно из чисел 1, 2, 3, 4. Из равенства 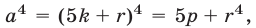 где
где 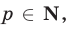 следует, что остаток от деления
следует, что остаток от деления 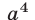 на
на 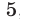 равен остатку от деления
равен остатку от деления 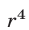 на
на 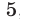 . Так как
. Так как 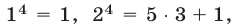
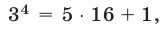
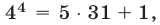 , то остаток от деления
, то остаток от деления 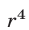 на
на 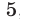 при
при 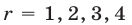 равен
равен 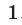 . Поэтому остаток от деления
. Поэтому остаток от деления 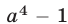 на
на 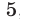 равен нулю, т.е. число
равен нулю, т.е. число 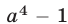 делится на
делится на 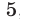 , если
, если 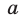 не делится на
не делится на  .
.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Примеры решения нелинейных систем неравенств с двумя переменными |
| Прямые и обратные теоремы примеры с решением |
| Метод математической индукции примеры с решением |
| Рациональные числа примеры с решением |
