Оглавление:

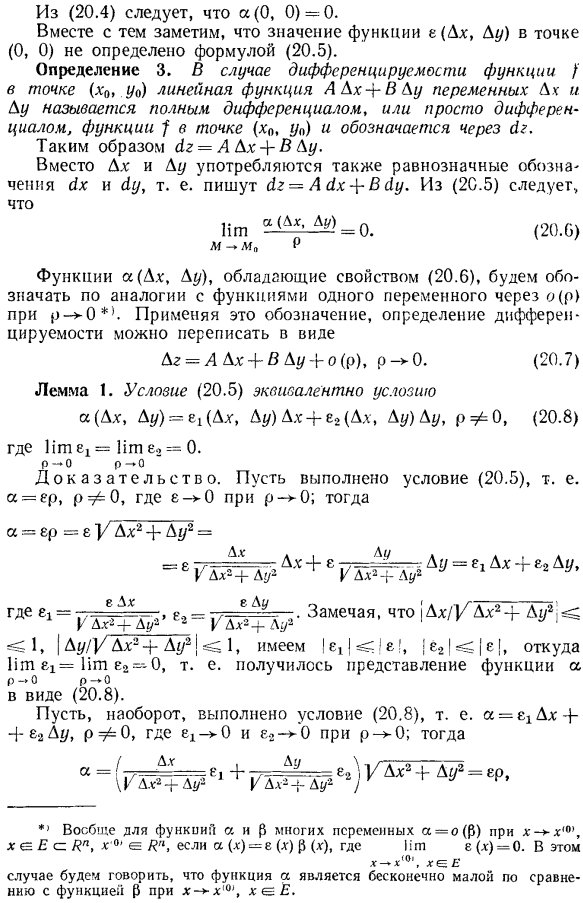







Дифференцируемость функций в точке
Дифференцируемость функций в точке. Во-первых, рассмотрим случай функции из 2 переменных. Функция r = [(x, y)=6 соседей И =(Y(M0; 6) точек M0 =(x0, Yo) и пусть (рис. 88) И так оно и есть.、 Наконец, пусть ДТ = Ф(н0 + ДХ, У0 + АУ) −1(х0, УО). Обычно Dg называется полным приращением функции. Определение 2.Функция r = f (x, y) называется дифференцируемой в точках (x0, y0), если имеется 2 числа A и B. Из (20.4), a (0, 0)= 0. В то же время следует отметить, что значение функции e (Ax, Du) в точках (0, 0) не определяется формулой (20.5). Определение 3.In в случае Дифференцируемости функции f ’в точке (x0, yo) линейные функции AAA-+ VAy переменных Ax и Ay называются суммарной производной функции/точки (xn, y), или просто дифференцированием.
Это название объясняется здесь тем, что, вообще говоря, все независимые переменные получают ненулевые приращения. Людмила Фирмаль
- Итак, yr = A Ax + VAu. Вместо Ah и Du, эквивалентные обозначения yx и yy также являются used. In другими словами, он описывает yg = a yx + B yu. (2С. 5) от Функция a (Ax, Ay) со свойством (20.6) обозначается через o (p как p-0*’) в силу ее сходства с функциями переменной 1.Используя эту нотацию, определение Дифференцируемости является Лемма 1.Условие(20.5)эквивалентно условию Доказательство. Предположим, что условие (20.5) выполнено. То есть a = ep, p 0.Где p-0 это e * 0.И затем… Здесь ex=■, E _ = YES {/заметил это! Dн / Udh2 + Au2 gs 1 / / Ду / Удх3 / −2121 =5 = 1 b! | | / = = = \ е!, / Е2 | | / / / Е|, где Mn&1 = Hm e2—0, то есть представление функции a (20.8) в формате. Напротив, мы предполагаем, что условие (20.8) выполняется. То есть a = e1Dx + + e2Dy, p => 0、 Так что для p-0 это e-0.Таким образом, получено представление функции a в виде (20.5). Тс Теорема 1.Если функция r=} (x, y) дифференцируема по точкам (x0, Yo), то она непрерывна в этой точке.
Действительно, поскольку| Dx / = = dr и| г / / <p, из уравнений (20.4) и (20.5) становится Д-> 0 для ρ-0, что означает непрерывность точек функции/(x0, y0). Теорема 2.Если функция r = f (x, y) дифференцируема в точке (xn, y0), а G = Ax + By является производной в этой точке, то в точке (x0, yo) y функция/является производной со всеми факторами. Подобный этому Доказательство. Определение Дифференцируемости ((20.4) и (20.8)) Предполагая Au = 0, Dt = Dl-r = A Ax + ex Dl. Вы получите: (Предполагая Au-0, p =.== |Длг [), так что это следует из (20.11).Отсюда Где для Dx* −0 правая сторона стремится к пределу, равному A. So, на левой стороне Dx-0 Также существует такое же ограничение, которое означает (x0, y0) в точке (20.1) private Производная равна = L. аналогично, если вы зададите Dx = 0 в(20.4) и передадите его до предела, то в D-0 это будет〜= B. Ts Если результирующая функция f (x, y) дифференцируема по точкам (Xo, Yo), то существует единственная производная.
- Единственность производной получается непосредственно из Формулы (20.9). Это происходит потому, что частная производная в определенной точке определяется однозначно. Напомним определение частной производной (см. (20.2)), а формулу (20.10) можно переписать в виде: То есть совершенная производная функции(если она существует) является суммой ее частных производных. Заметим, что утверждение противоположности теоремы 2 не выполняется. Существует функция со всеми частными производными во всех точках плоскости, но она не может быть дифференцирована в некоторых точках. point. An примером может служить функция (20.3) в конце предыдущего раздела. Для точек (0, 0) эта функция не является непрерывной, и по теореме 1 даже точки (0, 0) не дифференцируемы.
Из того, что было сказано, вы можете видеть, что выражение dxr-\-arcs не всегда является идеальной производной функции, если это имеет смысл. Сформулируйте достаточные условия для характеристики частных производных функции. Теорема 3.Поместите функцию r = [(x, y) в окрестности Частный дифференциал точек(x0, y°) Если она непрерывна в точке (x0, yn), то функция r = [(x, y) дифференцируема в этом отношении. Если результирующая функция r-f (x, y) имеет частные производные^и〜в окрестности точек (x0, y0), то далее они являются.
Связь между дифференцируемостью функции в определенной точке и наличием частных производных в этом отношении сложнее, чем связь между дифференцируемостью и существованием производной функции от 1 переменной. Людмила Фирмаль
- Частичная производная непрерывна в самой точке (x0, y°), поэтому функция r {(x, y) также непрерывна в этой точке. Доказательство теоремы. 11 (8) указывает окрестности точки B (x0, y0), где функция/определена с ее частными производными и и/ y. выберите Ax и A y, чтобы быть (x0 + Ax, r / 0 + Ay) E V(b).Я заметила. Он применяется к выражению, заключенному в квадратные скобки, является приращением функции только 1 переменной и является формулой конечного лагранжева приращения (см.§ 11.2).Это возможно потому, что функция f (V, yn + Ay), которая считается функцией 1 переменной x, находится в интервале, заканчивающемся в точках xn и Xo + Ax.
Смотрите также:
