Оглавление:
Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси
Пусть твердое тело под действием приложенных к нему внешних сил
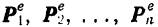
вращается вокруг неподвижной оси 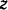 (рис. 200) с угловой скоростью
(рис. 200) с угловой скоростью  .
.
По теореме об изменении кинетического момента системы (формула (179)) имеем:
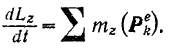
Но согласно формуле (177) кинетический момент твердого тела относительно его оси вращения равен
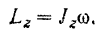
Подставляя это значение 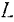 в предыдущее уравнение, находим:
в предыдущее уравнение, находим:
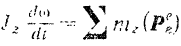
Обозначим через 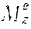 главный момент всех внешних сил, приложенных к твердому телу, относительно оси
главный момент всех внешних сил, приложенных к твердому телу, относительно оси 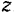 :
:
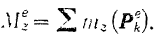
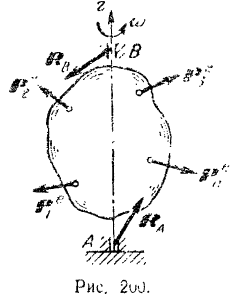
Принимая во внимание известные из кинематики зависимости, уравнение можно придать следующую форму:
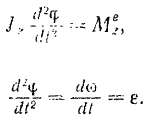
Произведении момента инерции тела относительно его оси вращения на угловое ускорение тела равно главному моменту всех приложенных телу внешних сил относительно той же оси.
Уравнение (182) называется дифференциальным уравнением вращательного движения твердого тела.
Так как момент инерции 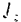 тела относительно данной оси есть величина постоянная, то, как это видно из уравнения (182). при постоянном главном моменте
тела относительно данной оси есть величина постоянная, то, как это видно из уравнения (182). при постоянном главном моменте 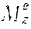 внешних сил угловое ускорение к есть величина постоянная. т. е. тело совершает равномерно переменное вращение.
внешних сил угловое ускорение к есть величина постоянная. т. е. тело совершает равномерно переменное вращение.
Из того же уравнения следы, что если приложенный к телу главный момент 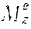 равен нулю, то угловое ускорение тела также равно нулю, т.е. тело либо остается в покое (если оно находилось в нем до того), либо вращается с постоянной угловой скоростью.
равен нулю, то угловое ускорение тела также равно нулю, т.е. тело либо остается в покое (если оно находилось в нем до того), либо вращается с постоянной угловой скоростью.
Нетрудно заметить, что но своему виду дифференциальное уравнение (.182) вращательного движения тела напоминает основное уравнение (106) динамики для материальной точки (или, что го же, для поступательного движения тела):
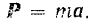
В уравнении (182) вместо силы 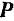 стоит главный момент внешних сил относительно оси вращения тела
стоит главный момент внешних сил относительно оси вращения тела 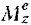 , вместо массы
, вместо массы 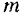 — момент инерции
— момент инерции 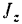 тела относительно оси вращения, вместо ускорения
тела относительно оси вращения, вместо ускорения 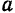 — угловое ускорение
— угловое ускорение 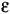 .
.
Из сопоставления уравнений (182) и (106) видно, что момент инерции тела играет при его вращательном движении ту же роль, что и масса тела при поступательном движении. Так же как масса тела является мерой инертности тела при его поступательном движении, так и момент инерции тела относительно данной оси является мерой инертности тела при его вращательном движении вокруг этой оси.
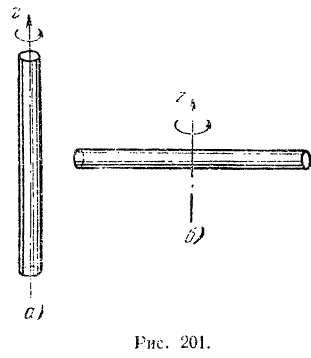
При одном и том же вращающем моменте угловое ускорение тела будет тем меньше, чем больше момент инерции тела относительно оси вращения. Существенное отличие момента инерции тела or его массы заключается, однако, в том. что масса тела является для него величиной постоянной, тогда как момент инерции тела зависит не только от самой вращающейся массы, по и от распределения этой массы относительно оси вращения. Например, одну и ту же длинную палку значительно легче привести руками в быстрое вращение вокруг ее продольной оси (рис. 201,а), чем вокруг оси, перпендикулярной к ее длине (рис. 201,6). Объясняется это тем, что в первом случае момент инерции палки
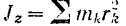
значительно меньше, чем во втором. Поэтому, для сообщения палке одинакового углового ускорения в первом случае потребуется значительно меньший вращающий момент.
Колесо с тяжелым ободом и легкой втулкой будет обладать большим моментом инерции, чем колесо той же массы, но с тяжелой втулкой и легким ободом, так как а первом случае большая часть массы находится на большем расстоянии от оси вращения. А так как чем значительнее момент инерции тела, тем труднее изменить сто движение, то этим и пользуются в маховиках, служащих для выравнивания хода машин, делая их значительного диаметра и распределяя большую часть их массы по ободу.
Уравнение (182) позволяет решать для вращательного движения тела вокруг неподвижной оси обе основные задачи динамики, т.е. позволяет: 1) зная уравнение вращения тела

и момент инерции 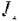 , относительно оси вращения, находить приложенный к телу главный момент сил
, относительно оси вращения, находить приложенный к телу главный момент сил
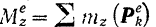
и, наоборот, 2) зная приложенные к телу внешние силы, момент инерции тола и начальные условия 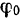 и
и 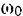 , находить как уравнение вращения тела, так и его угловую скорость и угловое ускорение.
, находить как уравнение вращения тела, так и его угловую скорость и угловое ускорение.
Надо заметить, что если решение первой задачи, в общем случае, сводится к простому дифференцированию функции
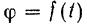
то решение второй задачи методом интегрирования уравнения (182) может представлять значительные трудности. В общем случае, главный момент сил 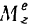 может быть величиной переменной, зависящей не только от времени, но еще и от угла поворота и угловой скорости тела.
может быть величиной переменной, зависящей не только от времени, но еще и от угла поворота и угловой скорости тела.
Пример задачи:
Для нахождения момента сил трения в подшипниках на вал насажен маховик весом 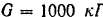 и ему сообщена угловая скорость
и ему сообщена угловая скорость 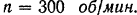 . Предоставленный самому себе маховик останавливается через
. Предоставленный самому себе маховик останавливается через 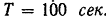 Радиус инерции маховика
Радиус инерции маховика 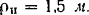 . Определить момент трения, считая его постоянным.
. Определить момент трения, считая его постоянным.
Решение:
Согласно основному уравнению (182) для вращательного движения твердого тела
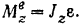
Приложенный к маховику момент трения постоянен, поэтому вращение маховика будет равномерно переменным. Угловое ускорение равномерно переменного вращения определяется из формулы (89)
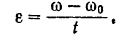
В нашем случае при
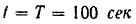
угловая скорость маховика
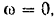
начальная же его угловая скорость
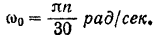
Отсюда угловая ускорение маховика
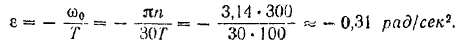
Знак минус показывает, что мы в данном случае имеем замедленное вращение.
Момент инерции маховика находим по формуле (141)
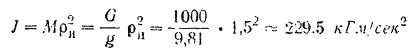
Следовательно, искомый момент трения будет равен
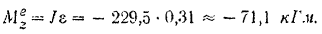
Знак момента трения говорит о том, чю он направлен в сторону, противоположную вращению маховика.
Пример задачи:
Шкив (рис. 202) получает вращение от другого ведущего! шкива при помощи ременной передачи. Ведущая ветвь ремня натянута с силой 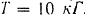 ведомая ветвь с силой
ведомая ветвь с силой 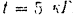 . Вес шкива
. Вес шкива 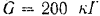 , его диаметр
, его диаметр 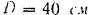 . Определить угловое ускорение шкива, принимая во внимание трение вала в подшипниках. Диаметр вала
. Определить угловое ускорение шкива, принимая во внимание трение вала в подшипниках. Диаметр вала 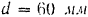 коэффициент трения
коэффициент трения 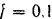 . Весом вала пренебречь. Шкив считать сплошным однородным цилиндром.
. Весом вала пренебречь. Шкив считать сплошным однородным цилиндром.
Решение:
Сила трения вала в подшипниках равна
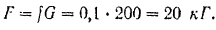
Главный момент 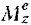 равен алгебраической сумме всех приложенных к шкиву внешних сил относительно оси
равен алгебраической сумме всех приложенных к шкиву внешних сил относительно оси 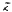 вращения тела:
вращения тела:
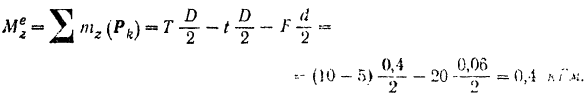
Момент инерции шкива находится но формуле (145)
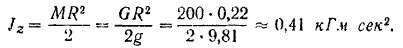
Зная приложенный к шкиву главный момент 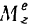 и его момент инерции относительно оси вращения, легко найти по дифференциальному уравнению (182) для вращательного движения тела и его угловое ускорение
и его момент инерции относительно оси вращения, легко найти по дифференциальному уравнению (182) для вращательного движения тела и его угловое ускорение
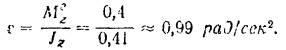
Пример задачи:
Судовой винт приводится по вращение из состояния покоя приложенным к нему постоянным вращающим моментом 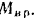 . Момент сил сопротивлений воды, действующих на винт,
. Момент сил сопротивлений воды, действующих на винт,
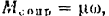
где 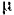 — некоторый постоянный коэффициент. Найти, как изменяется со временем угловая скорость винта к ее предельное значение. Момент инерции винта относительно его оси вращении равен
— некоторый постоянный коэффициент. Найти, как изменяется со временем угловая скорость винта к ее предельное значение. Момент инерции винта относительно его оси вращении равен 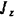 .
.
Решение:
Пишем дифференциальное уравнение (182) вращательного движения винта:
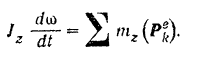
В нашем случае
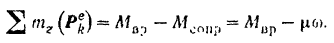
Следовательно,
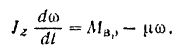
Разделяя переменные в этом уравнении и интегрируя его в соответствующих пределах, будем иметь:
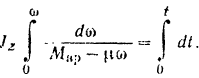
Отсюда находим
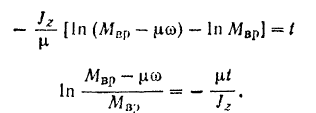
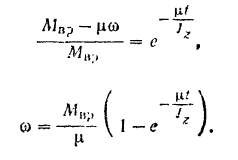
Так как величина
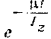
убывает с течением времени, асимптотически приближаясь к нулю, то угловая скорость 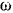 винта возрастает, асимптотически приближаясь к своему предельному значению
винта возрастает, асимптотически приближаясь к своему предельному значению
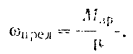
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
