Оглавление:
Таблица производных основных элементарных функций
Найдем, пользуясь известными из §4. пункт 3 предыдущей главы пределами и правилами дифференцирования из предшествующего параграфа, производные основных элементарных функций.
Сначала найдем производную натурального логарифма, воспользовавшись определением производной, числом е (глава IV, §4, пункт 3, формула (5)) и непрерывностью логарифмической функции (глава IV, §5. пункт 4):
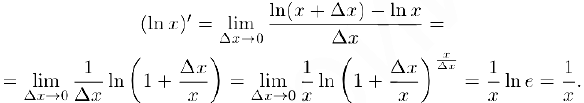
Таким образом, 
. Отсюда сразу же следует, что при любом 
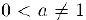
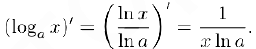
Теперь, использовав производную логарифма и правило дифференцирования композиции функций, мы найдем производные степенной и показательной функций. Рассмотрим сначала при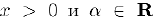 
степенную функцию 
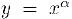. Последовательно прологарифмируем и продифференцируем обе части последнего равенства:
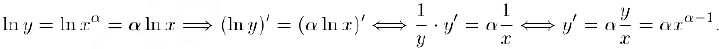
Стало быть.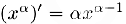 
. В частности, 
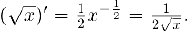Совершенно аналогично найдем производную показательной функции 
:
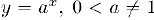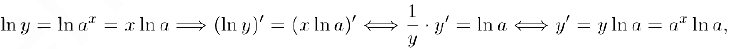
т.е.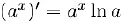 
. Отсюда, в частности, следует, что 
.
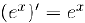Займемся теперь производными тригонометрических функций. Принимая во внимание тригонометрический предел (глава IV. §4. пункт 3, формулы (4)) и непрерывность функции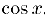 
, получим:
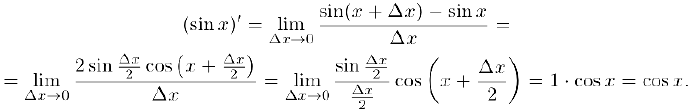
Отсюда, воспользовавшись правилом дифференцирования композиции функций, найдем:
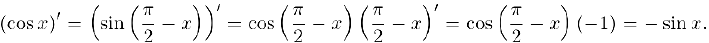
Найдем, используя правило дифференцирования частного. производные функций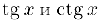 
:
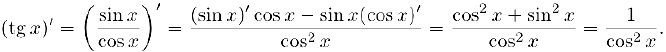
Аналогично.
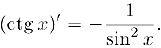
Осталось отыскать формулы для производных обратных тригонометрических функций. Для функции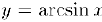 
мы имеем 
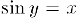. Дифференцируя обе части последнего равенства, получим:
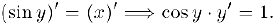
Отсюда.
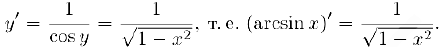
Учитывая далее, что при всех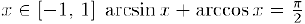 
находим:
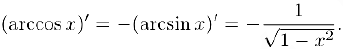
Совершенно аналогично мы можем проверить, что
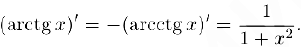
Приведем здесь еще формулы дифференцирования гиперболических функций, определенных в §4. пункт 1 главы IV.
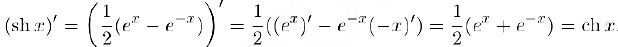
Аналогично мы можем убедиться в том, что
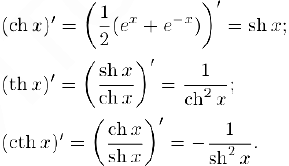
Сведем теперь все найденные производные в таблицу.
Таблица производных
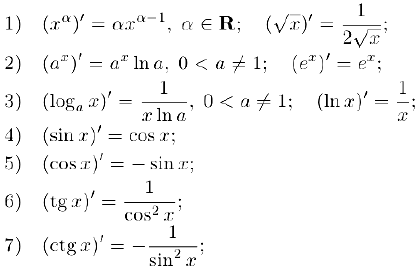
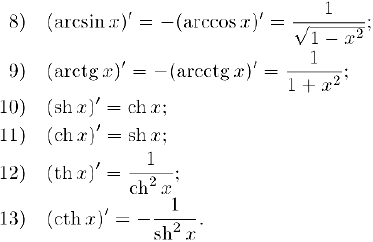
Используя эту таблицу и доказанные в предыдущем параграфе правила дифференцирования. мы можем найти производную любой элементарной функции, причем эта производная также будет элементарной функцией.
Дифференцирование функций, заданных неявно и параметрически
а) Производная неявно заданной функции.
Иногда бывае т трудно или невозможно установи ть явную, г. е. прямую зависимость между переменными х и у, однако сравнительно несложно найти связь между ними в виде уравнения
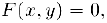
где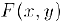 
— известная функция своих аргументов.
Функция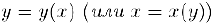 
, для которой в некотором интервале
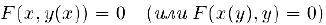
называется неявной функцией. определяемой уравнением (1).
В общем случае неявная функция определяется из уравнения (1) неоднозначно. гак как график неявной функции представляет собой, вообще1 говоря, лишь часть кривой, заданной уравнением (1). Например, из уравнения гиперболы
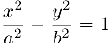
мы находим:
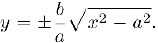
Таким образом, это уравнение определяет две неявные функции, определенные при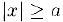 
. Предположим теперь, что неявная функция 
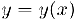, определяемая уравнением (1) дифференцируема в интервале, где она определена. Поскольку при всех х из интервала определения неявной функции 
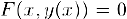, то формально ее производная может быть найдена из уравнения
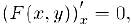
в котором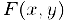 
рассматривается как сложная дифференцируемая функция аргумента x. Выполнив дифференцирование в уравнении (2), мы получим линейное относительно искомой производной 
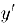уравнение, из которого она и определяется.
Производные и дифференциалы высших порядков
Определим в заключение этого параграфа понятия производной и дифференциала высших порядков.
Пусть функция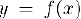
дифференцируема в интервале 
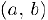и, таким образом, в этом интервале определена функция 
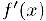. Если в точке 
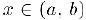существует производная функции 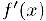. го она называется второй производной функции 
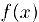(производной второго порядка) и обозначается через 
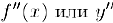. Таким образом.
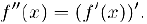
В этом случае функцию 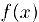будем называть дважды дифференцируемой в точке х.
Вторым дифференциалом (дифференциалам второго порядка) в точке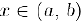 
, в которой существует вторая производная 
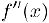, называется дифференциал от первого дифференциала. Для второго дифференциала используется обозначение 
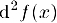. Учитывая, что 
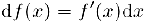и дифференциал аргумента 
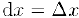не зависит от х, получим:
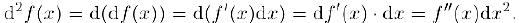
Следовательно,
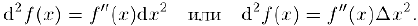
Аналогично находятся производные и. дифференциалы более высоких. порядков:
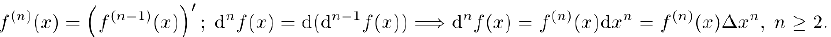
Из последней формулы следует, в частности, что для производной n-го порядка функции 
можно использовать обозначение
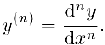
Если требуется явно указать переменную, по которой ведется дифференцирование, то производную n-го порядка функции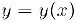 
мы будем обозначать через
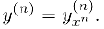
Пример 20.
Найти производную n-го порядка функции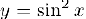 
.
Решение:
Чтобы заметить общую закономерность, найдем несколько первых производных данной функции:
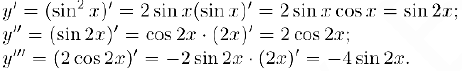
Исходя из структуры этих производных мы можем предположить, тго производная n-го порядка данной функции имеет вид:
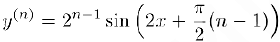
Проверим эту гипотезу по индукции. При n = 1 утверждение справедливо. Предположим, что оно верно для номера n и докажем, что оно имеет место также и для следующего номера n + 1. Действительно,
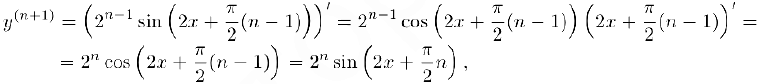
в чем и требовалось убедиться.
По индукции несложно убедиться в том. что производную n-го порядка произведения n раз дифференцируемых функций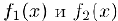 
мы можем найти по формуле Лейбница:
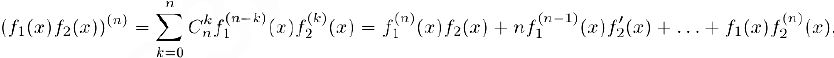
где
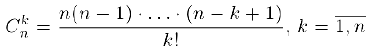
и по определению считается, что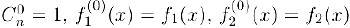 
.
Если функция задана неявно или параметрически (пункт 2). то повторным дифференцированием мы также можем находить производные высших порядков этой функции. Остановимся чуть подробнее на повторном дифференцировании параметрически заданной функции. Пусть функция задана параметрически уравнениями
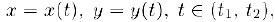
причем функции 
удовлетворяют всем условиям, перечисленным в пункте 2, b) и. сверх того, они дважды дифференцируемы в интервале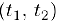 
. Тогда
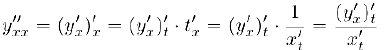
и, таким образом,
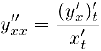
Аналогично мы можем найти и производные более высоких порядков параметрически заданной функции.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
