Оглавление:
Задача 2.77.
Для производства двух видов изделий А к В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Время обработки каждого из изделий на оборудовании данного типа приведено в табл. 2.50. В ней же указаны затраты, связанные с производством одного изделия каждого вида.

Оборудование I и III типов предприятие может использовать не более 26 и 39 ч. При этом оборудование II типа целесообразно использовать не менее 4 ч.
Требуется определить, сколько изделий каждого вида следует изготовить предприятию, чтобы себестоимость одного изделия была минимальной.
Решение:
Предположим, что предприятие изготовит 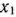 изделий вида
изделий вида 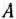 и
и 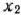 изделий вида
изделий вида 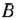 . Тогда общие затраты на их производство равны
. Тогда общие затраты на их производство равны 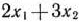 руб., а себестоимость одного изделия в рублях составит
руб., а себестоимость одного изделия в рублях составит
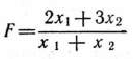
Затраты времени на обработку указанного количества изделий на каждом из типов оборудования соответственно составят 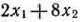 часов,
часов, 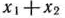 часов и
часов и 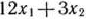 часов. Так как оборудование I и III типов может быть занято обработкой изделий вида
часов. Так как оборудование I и III типов может быть занято обработкой изделий вида 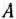 и
и 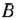 не более 26 и 39 ч, а оборудование II типа — не менее 4 ч, то должны выполняться следующие неравенства:
не более 26 и 39 ч, а оборудование II типа — не менее 4 ч, то должны выполняться следующие неравенства:
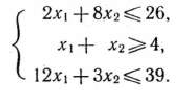
По своему экономическому смыслу переменные 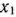 и
и 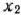 могут принимать только лишь неотрицательные значения:
могут принимать только лишь неотрицательные значения:
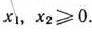
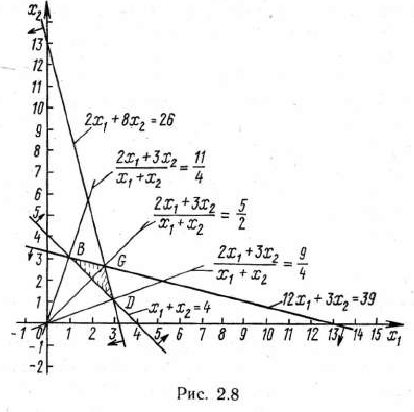
Таким образом, математическая постановка задачи состоит в определении неотрицательного решения системы линейных неравенств (97), реализующего минимум функции (96). Чтобы найти решение задачи, прежде всего построим многоугольник решений. Как видно из рис. 2.8, им является треугольник 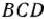 . Значит, функция (96) принимает минимальное значение в одной из точек:
. Значит, функция (96) принимает минимальное значение в одной из точек: 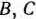 или
или 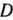 . Чтобы определить, в какой именно, положим значение функции
. Чтобы определить, в какой именно, положим значение функции 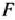 равным некоторому числу, например 11/4. Тогда
равным некоторому числу, например 11/4. Тогда
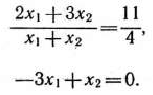
Уравнение (99) определяет прямую, проходящую через начало координат. Координаты точек, принадлежащих этой прямой
и многоугольнику решений, являются планами задачи, при которых значение функции (96) равно 11/4. В данном случае к указанным точкам относится лишь одна точка 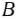 (1; 3). Ее координаты определяют план задачи, при котором значение функции равно 11/4.
(1; 3). Ее координаты определяют план задачи, при котором значение функции равно 11/4.
Возьмем теперь 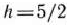 , т.е. положим
, т.е. положим
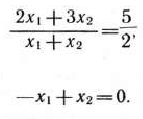
Уравнение (100), так же как и (99), определяет прямую, проходящую через начало координат. Ее можно рассматривать как прямую, полученную в результате вращения по часовой стрелке вокруг начала координат прямой (99).
При этом координаты точек, принадлежащих прямой (100) и многоугольнику решений, являются планами задачи, при которых значение функции (96), равное 5/2, меньше, чем в точках прямой (99).
Следовательно, если положить значение функции (96) равным некоторому числу 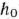 :
:
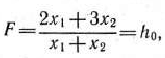
а прямую (101), проходящую через начало координат, вращать в направлении движения часовой стрелки вокруг начала координат, то получим прямые
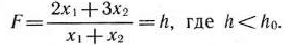
Найдем последнюю общую точку вращаемой прямой с многоугольником решении. Это точка 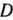 (3; 1) (рис. 2.8), в которой достигается минимум функции (96).
(3; 1) (рис. 2.8), в которой достигается минимум функции (96).
Таким образом, оптимальным планом производства продукции является план, согласно которому изготовляется три изделия вида 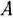 и одно изделие вида
и одно изделие вида 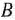 . При таком плане себестоимость одного изделия является минимальной и равна
. При таком плане себестоимость одного изделия является минимальной и равна
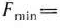
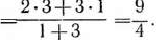
При нахождении угловой точки многоугольника решений, в которой целевая функция задачи принимает наименьшее значение, мы полагали значение функции равным некоторым двум постоянным числам и установили направление вращения прямой, определяющее уменьшение значения функции. Это можно было сделать и по-другому. А именно: полагая значение функции 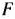 равным некоторому числу т. е.
равным некоторому числу т. е.
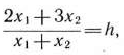
и получив некоторую прямую, проходящую через начало координат и имеющую угловой коэффициент, зависящий от 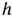 можно, используя производную, установить направление вращения прямой (102) при возрастании
можно, используя производную, установить направление вращения прямой (102) при возрастании 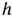 .
.
Практически же дело обстоит гораздо проще. Найдя точки 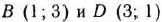 (рис. 2.8), в которых функция (96) может принимать минимальное значение, вычислим ее значения в этих точках:
(рис. 2.8), в которых функция (96) может принимать минимальное значение, вычислим ее значения в этих точках: 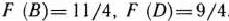 . Так как
. Так как 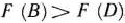 , то можно утверждать, что в точке
, то можно утверждать, что в точке 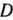 целевая функция принимает минимальное значение. Одновременно с этим заметим, что в точке
целевая функция принимает минимальное значение. Одновременно с этим заметим, что в точке 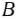 функция
функция 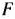 принимает максимальное значение.
принимает максимальное значение.
Заканчивая рассмотрение нахождения решения задачи дробно-линейного программирования графическим методом, отметим, что при решении конкретных задач могут быть различные случаи.
- Многогранник решений ограничен, максимум и минимум достигаются в его угловых точках (рис. 2.9).
- Многогранник решений не ограничен, однако существуют угловые точки, в которых целевая функция задачи принимает соответственно максимальное и минимальное значения (рис. 2.10)
- Многогранник решений не ограничен, и один из экстремумов достигается.
- Задача (105)—(108) является задачей линейного программирования, а следовательно, ее решение можно найти известными методами. Зная оптимальный план этой задачи, на основе соотношений (104) получаем оптимальный план исходной задачи (92) —(94).
Таким образом, процесс нахождения решения задачи дробно-линейного программирования включает следующие этапы:
- Сводят задачу (92)—(94) к задаче линейного программирования (105) — (108).
- Находят решение задачи (105) — (108).
- Используя соотношения (104), определяют оптимальный план задачи (92) —(94) и находят максимальное значение функции (92).
Задача 2.84.
Найти максимальное значение функции
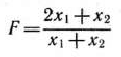
при условиях
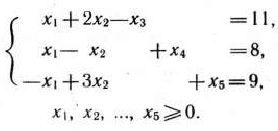
Решение:
Сведем данную задачу к задаче линейного программирования. Для этого обозначим 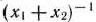 через
через 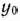 и введем новые переменные
и введем новые переменные 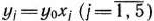 . В результате приходим к следующей задаче: найти максимум функции
. В результате приходим к следующей задаче: найти максимум функции
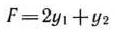
при условиях
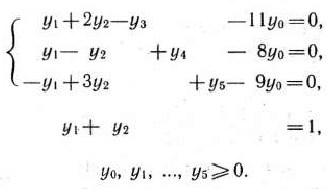
Задача (112)—(114) является задачей линейного программирования. Ее решение находим методом искусственного базиса (табл. 2.51).
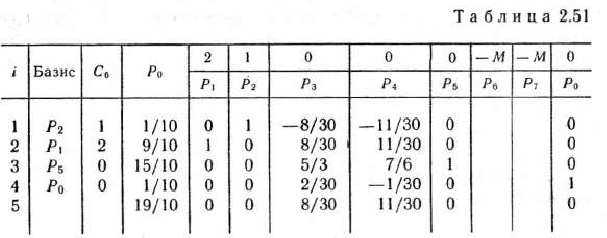
Из табл. 2.51 видно, что оптимальным планом задачи (112) — (114) является
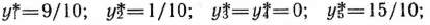
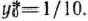
Учитывая, что
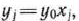
находим оптимальный план задачи (109) —(111):
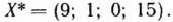
При этом плане
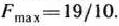
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
