Оглавление:
Задача 2.67.
Для производства продукции трех видов 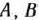 и
и 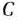 необходимы три различных вида сырья. Каждый из видов сырья может быть использован в объеме, соответственно не большем чем 180, 210 и 244 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции данного вида приведены в табл. 2.44.
необходимы три различных вида сырья. Каждый из видов сырья может быть использован в объеме, соответственно не большем чем 180, 210 и 244 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции данного вида приведены в табл. 2.44.

Определить план производства продукции, обеспечивающий максимальный выпуск ее в стоимостном выражении, и провести анализ устойчивости оптимального плана относительно возможных изменений объемов каждого из используемых видов сырья.
Решение:
Предположим, что изделий вида 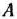 производится
производится 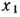 единиц, изделий вида
единиц, изделий вида  единиц и изделий вида
единиц и изделий вида  единиц. Тогда для определения оптимального плана производства нужно решить задачу, состоящую в максимизации целевой функции
единиц. Тогда для определения оптимального плана производства нужно решить задачу, состоящую в максимизации целевой функции
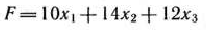
при условиях
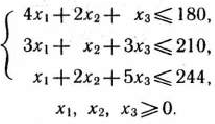
Решение задачи (83)—(85) симплексным методом приведено в табл. 2.45.
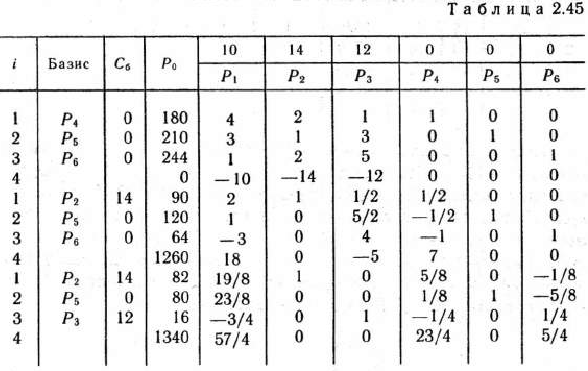
Из этой таблицы видно, что при оптимальном плане производства изделий должно быть изготовлено 82 изделия вида  и 16 изделий вида
и 16 изделий вида 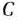 . При данном плане общая стоимость изделий равна 1340 руб.
. При данном плане общая стоимость изделий равна 1340 руб.
Проведем теперь анализ устойчивости найденного плана относительно возможных изменений сырья каждого вида. Начнем с сырья I вида. Предположим, что производство изделий ограничено не 180 кг сырья I вида, а 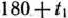 кг, где
кг, где 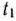 — некоторый параметр, который в общем случае может принимать как положительные, так и отрицательные значения. Таким образом, следует найти такие значения параметра
— некоторый параметр, который в общем случае может принимать как положительные, так и отрицательные значения. Таким образом, следует найти такие значения параметра 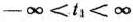 , при которых задача, состоящая в определении максимального значения функции
, при которых задача, состоящая в определении максимального значения функции
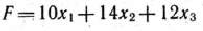
при условиях
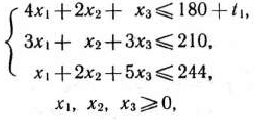
имеет оптимальный план
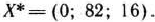
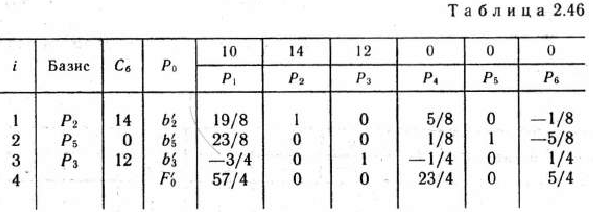
Найдем решение задачи параметрического программирования (86) —(88). При каждом значении параметра 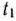 оптимальный план задачи (86) — (88) определяется из табл. 2.46, отличающейся от последней симплекс-таблицы (табл. 2.45) лишь элементами столбца вектора
оптимальный план задачи (86) — (88) определяется из табл. 2.46, отличающейся от последней симплекс-таблицы (табл. 2.45) лишь элементами столбца вектора 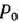 , которые обозначим через
, которые обозначим через 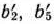 и
и 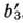 . Указанные числа представляют собой компоненты разложения вектора
. Указанные числа представляют собой компоненты разложения вектора 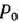 по векторам, образующим последний базис, т. е. по векторам
по векторам, образующим последний базис, т. е. по векторам 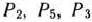 . Следовательно,
. Следовательно,
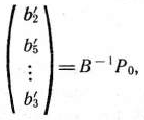
где 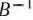 — матрица, обратная матрице
— матрица, обратная матрице 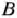 , составленной из первоначальных компонент векторов
, составленной из первоначальных компонент векторов 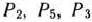 . Указанная матрица
. Указанная матрица 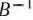 записана в симплекс-таблице (табл. 2.46) в столбцах векторов, образующих первоначальный единичный базис, т. е. в столбцах векторов
записана в симплекс-таблице (табл. 2.46) в столбцах векторов, образующих первоначальный единичный базис, т. е. в столбцах векторов 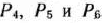 . Таким образом,
. Таким образом,
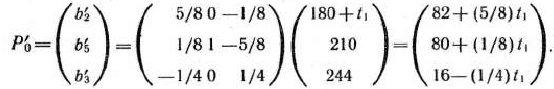
Найденный вектор 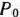 определяет оптимальный план
определяет оптимальный план 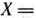
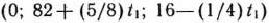 задачи (86) —(88) для любого значения параметра 1), при котором значения
задачи (86) —(88) для любого значения параметра 1), при котором значения 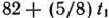 ,
, 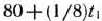 и
и 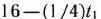 положительны. Вместе с тем
положительны. Вместе с тем  будет совпадать с оптимальным планом
будет совпадать с оптимальным планом 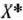 =(0; 82; 16) задачи (83) — (85) лишь при значении
=(0; 82; 16) задачи (83) — (85) лишь при значении 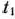 =0. Это означает, что всякое, хотя бы самое незначительное, изменение объемов сырья I вида приведет к изменению оптимального плана задачи (83) — (85). Например, если имеющиеся в распоряжении предприятия объемы сырья I вида увеличить на 8 ед., то оптимальным планом производства продукции является план
=0. Это означает, что всякое, хотя бы самое незначительное, изменение объемов сырья I вида приведет к изменению оптимального плана задачи (83) — (85). Например, если имеющиеся в распоряжении предприятия объемы сырья I вида увеличить на 8 ед., то оптимальным планом производства продукции является план 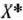 = (0; 82+(5/8)-8; 16 —(1/4)-8) = = (0; 87; 14), согласно которому изготовляется 87 изделий вида
= (0; 82+(5/8)-8; 16 —(1/4)-8) = = (0; 87; 14), согласно которому изготовляется 87 изделий вида 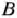 и 14 изделий вида
и 14 изделий вида 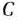 . При данном плане производства продукции общая стоимость изготовляемых изделий составит 1386 руб. т. е. возрастет на 46 руб.
. При данном плане производства продукции общая стоимость изготовляемых изделий составит 1386 руб. т. е. возрастет на 46 руб.
Проведя аналогичные рассуждения, можно показать, что если объемы сырья 11 вида, выделенные предприятию, уменьшить не более чем на 80 кг. то оптимальным планом производства продукции останется план, согласно которому следует изготовить 82 изделия вида 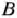 и 16 изделий вида
и 16 изделий вида 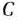 . Таким образом, оптимальный план задачи (83)—(85) оказывается устойчивым относительно изменений в указанных выше объемах сырья II вида.
. Таким образом, оптимальный план задачи (83)—(85) оказывается устойчивым относительно изменений в указанных выше объемах сырья II вида.
Наконец, аналогично можно показать, что оптимальный план 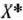 = (0; 82; 16) задачи (83) — (85) не устойчив по отношению к изменениям объемов сырья III вида.
= (0; 82; 16) задачи (83) — (85) не устойчив по отношению к изменениям объемов сырья III вида.
Мы провели анализ чувствительности оптимального плана задачи (83)—(85) к изменению объемов каждого из видов сырья по отдельности. Аналогично можно провести анализ чувствительности оптимального плана этой задачи при одновременном изменении объемов сырья нескольких видов.
Решение задачи, целевая функция и правые части ограничений которой содержат параметр. Используя описанные выше алгоритмы решения задач параметрического программирования, можно найти решение задачи, в которой от параметра t линейно зависят как коэффициенты целевой функции, так и свободные члены системы уравнений.
Задача 2.68.
Найти максимальное значение функции
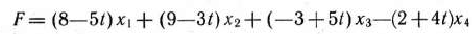
при условиях
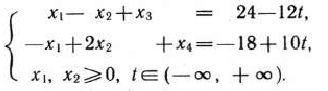
Решение:
Считая значение параметра 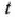 равным числу 2 (число 2 взято произвольно), находим симплексным методом решение полученной задачи линейного программирования (табл. 2.47).
равным числу 2 (число 2 взято произвольно), находим симплексным методом решение полученной задачи линейного программирования (табл. 2.47).

Из табл. 2.47 видно, что если
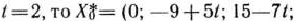
оптимальный план задачи. Таким он является и для тех значений параметра 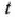 , при которых
, при которых
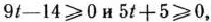
а среди компонент вектора 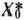 нет отрицательных чисел. Эти неравенства выполняются при
нет отрицательных чисел. Эти неравенства выполняются при 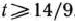 . Сначала такие значения параметра
. Сначала такие значения параметра 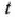 и рассмотрим.
и рассмотрим.
Найденный вектор 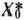 является оптимальным планом задачи при
является оптимальным планом задачи при
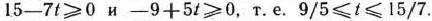
Итак, если
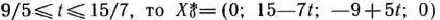
оптимальный план задачи, при котором
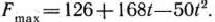
Если
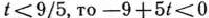
вектор 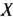 =(0; 15—7/;—9 + 5/; 0) не является планом задачи. Поэтому при
=(0; 15—7/;—9 + 5/; 0) не является планом задачи. Поэтому при 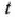 <9/5 следует перейти к новой симплекс-таблице, что можно сделать, так как в строке вектора
<9/5 следует перейти к новой симплекс-таблице, что можно сделать, так как в строке вектора 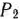 (табл. 2.47) имеется отрицательное число — 1/2. Рассматривая это число как разрешающий элемент, переходим к новой симплекс-таблице, для чего исключим из базиса вектор
(табл. 2.47) имеется отрицательное число — 1/2. Рассматривая это число как разрешающий элемент, переходим к новой симплекс-таблице, для чего исключим из базиса вектор 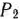 и введем вместо него вектор
и введем вместо него вектор 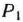 (табл. 2.48).
(табл. 2.48).

Из табл. 2.48 видно, что вектор
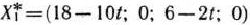
есть оптимальный план задачи для всех значений параметра 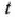 (как отмечено выше, мы рассматриваем значения
(как отмечено выше, мы рассматриваем значения 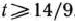 ), при которых
), при которых
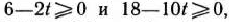
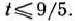
Следовательно, если
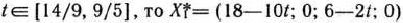
является оптимальным планом задачи, при котором
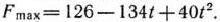
Рассмотрим теперь значения параметра 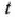 > 15/7. При этих значениях вектор
> 15/7. При этих значениях вектор
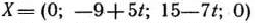
уже не является оптимальным планом задачи, поскольку 15—7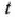 <0. Так как в строке вектора
<0. Так как в строке вектора  (табл. 2.48) нет отрицательных чисел, то при
(табл. 2.48) нет отрицательных чисел, то при 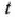 > 15/7 задача неразрешима.
> 15/7 задача неразрешима.
Мы нашли решение задачи при изменении параметра 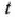 от 14/9 до
от 14/9 до 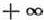 . Рассмотрим теперь значения параметра от
. Рассмотрим теперь значения параметра от 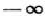 до 14/9. Если
до 14/9. Если 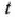 < 14/9, то в последней строке табл. 2.48 имеется отрицательное число 18
< 14/9, то в последней строке табл. 2.48 имеется отрицательное число 18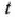 —28. Поэтому следует перейти к новому опорному плану, введя в базис вектор
—28. Поэтому следует перейти к новому опорному плану, введя в базис вектор 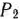 и исключив из него вектор
и исключив из него вектор 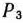 (табл. 2.49).
(табл. 2.49).

Из табл. 2.49 видно, что если
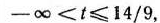
то
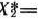
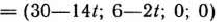
является оптимальным планом задачи, причем
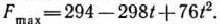
Итак, при
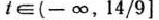
задача имеет оптимальный план
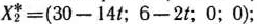
при
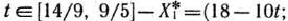
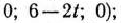
при
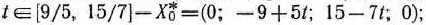
при
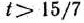
она неразрешима.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
