Оглавление:
Достаточное условие дифференцируемости
Если функция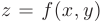 
обладает непрерывными частными производными 
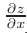и 
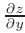в данной области, то эта функция дифференцируема в этой области и дифференциала ее дифференциал выражается формулой
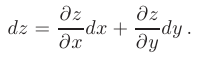
В силу определения дифференциала при малых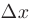 
и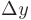 
приращение дифференцируемой функции можно приближенно заменить ее дифференциалом. Отсюда имеем приближенное равенство
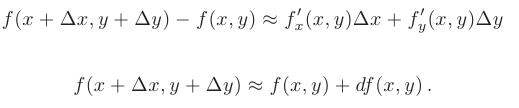
Пример:
Задана функция двух переменных и две точки:
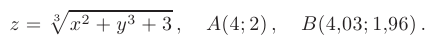
Вычислить: 1) приближенное значение функции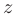 
в точке 
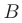с помощью дифференциала 
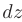; 2) значение функции 
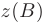непосредственно, без помощи дифференциала; 3) относительную погрешность (в процентах), возникающую при замене приращения функции 
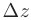ее дифференциалом 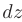в точке .
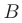► 1. Найдем частные производные функции :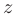
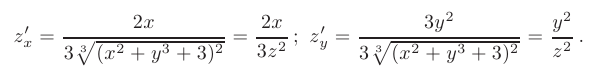
Подставляя координаты точки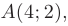 
получим:
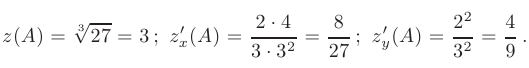
При
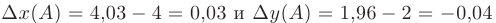
найдем дифференциал функции в точке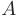 
:
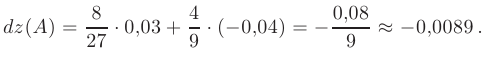
Далее по формуле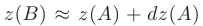 
находим приближенное значение функции 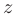в точке :
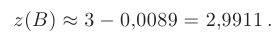
- Вычислим теперь значение функции в точке В непосредственно:
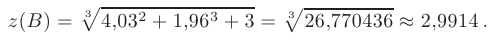
- Заметим, что если
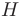— точное, a 
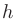— приближенное значение некоторой величины, то относительная погрешность приближенного значения 
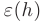в процентах определяется по формуле:
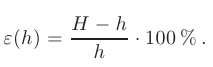
В данном случае относительная погрешность приближенного значения 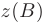равна:
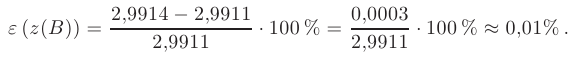
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Непрерывность и частные производные в математике |
| Полное приращение и дифференциал в математике |
| Производная по направлению и градиент в математике |
| Экстремум функции двух переменных в математике |
