Оглавление:
Достаточность
Пусть в области 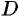 выполняется условие (48.19). Покажем, что существует функция
выполняется условие (48.19). Покажем, что существует функция 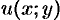 в области
в области 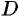 такая, что
такая, что
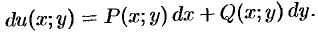
Найдем эту функцию. Искомая функция должна удовлетворять требованиям:
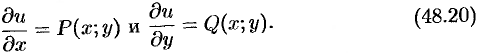
Если в первом уравнении (48.20) зафиксировать  и проинтегрировать его по
и проинтегрировать его по  , то получим:
, то получим:
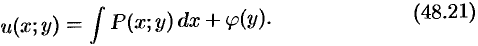
Здесь произвольная постоянная 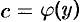 зависит от
зависит от  (либо является числом). В решении (48.21) не известна лишь
(либо является числом). В решении (48.21) не известна лишь 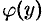 . Для ее нахождения продифференцируем функцию (48.21) по
. Для ее нахождения продифференцируем функцию (48.21) по  :
:
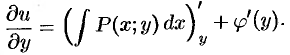
Используя второе равенство (48.20), можно записать:
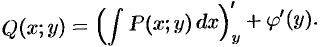
Отсюда
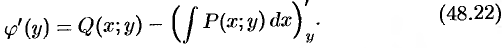
В равенстве (48.22) левая часть зависит от  . Покажем, что и правая часть равенства зависит только от
. Покажем, что и правая часть равенства зависит только от  .
.
Для этого продифференцируем правую часть по  и убедимся, что производная равна нулю. Действительно,
и убедимся, что производная равна нулю. Действительно,
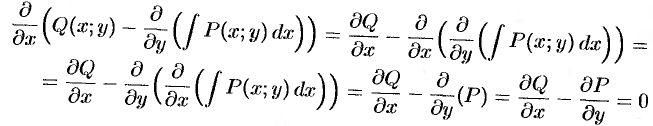
в силу условия (48.19).
Из равенства (48.22) находим 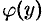 :
:
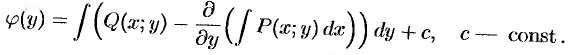
Подставляя найденное значение для 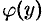 в равенство (48.21), находим функцию
в равенство (48.21), находим функцию 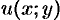 такую, что
такую, что 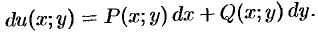
Таким образом, при решении ДУ вида (48.17) сначала проверяем выполнение условия (48.19). Затем, используя равенства (48.20), находим функцию 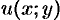 . Решение записываем в виде (48.18).
. Решение записываем в виде (48.18).
Пример №48.11.
Решить уравнение 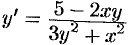 .
.
Решение:
Запишем уравнение в дифференциальной форме:
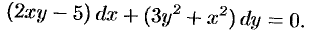
Здесь 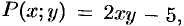
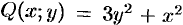 . Проверяем выполнение условия (48.19):
. Проверяем выполнение условия (48.19):
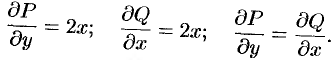
Следовательно, данное уравнение есть уравнение в полных дифференциалах. Условия (48.20) будут здесь выглядеть как
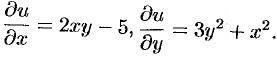
Отсюда имеем
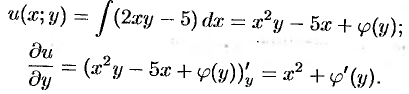
Далее
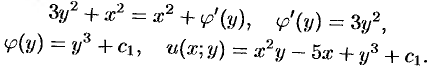
Общим интегралом является 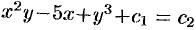 , или
, или 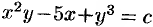 , где
, где 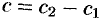 .
.
Если условие (48.19) не выполняется, то ДУ (48.17) не является уравнением в полных дифференциалах.
Однако это уравнение иногда можно привести к уравнению в полных дифференциалах умножением его на некоторую функцию 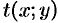 , называемую интегрирующим множителем.
, называемую интегрирующим множителем.
Чтобы уравнение 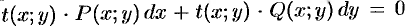 было уравнением в полных дифференциалах, должно выполняться условие
было уравнением в полных дифференциалах, должно выполняться условие
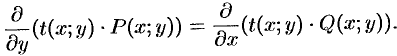
Выполнив дифференцирование 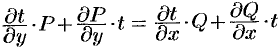 и приведя подобные слагаемые, получим
и приведя подобные слагаемые, получим
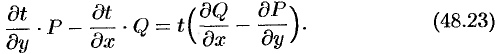
Для нахождения 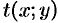 надо проинтегрировать полученное ДУ в частных производных. Решение этой задачи не простое. Нахождение интегрирующего множителя может быть упрощено, если допустить существование
надо проинтегрировать полученное ДУ в частных производных. Решение этой задачи не простое. Нахождение интегрирующего множителя может быть упрощено, если допустить существование 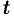 как функции только одного аргумента
как функции только одного аргумента  либо только
либо только  . Пусть, например,
. Пусть, например, 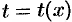 . Тогда уравнение (48.23) принимает вид
. Тогда уравнение (48.23) принимает вид
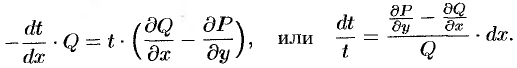
Отсюда
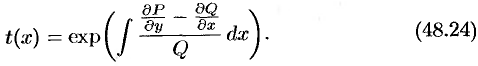
При этом выражение 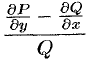 должно зависеть только от
должно зависеть только от  .
.
Аналогично получаем, что если 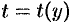 (
(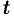 не зависит от
не зависит от  ), то
), то
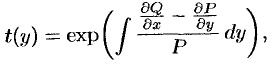
а подынтегральное выражение должно зависеть только от  .
.
Дополнительный пример №48.12.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
