Оглавление:


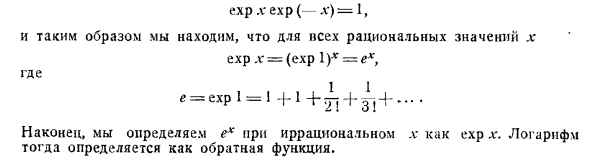
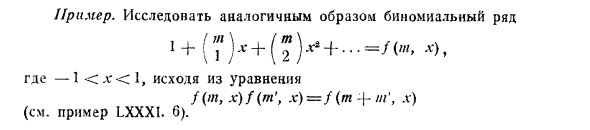
Другой способ развития теории показательной и логарифмической функций
- Еще один способ развития экспоненциальной и логарифмической теории. Вот краткий обзор другого метода для изучения свойств функций e * и lnx. Это сильно отличается от логической структуры, показанной на предыдущей странице. Этот метод происходит из экспоненциального ряда ! + * + £ + • ■ •• Поскольку мы знаем, что этот ряд сходится при всех значениях x, мы можем определить функцию expl. exp * = 1 +. (1)
Кроме того, LXXXI в качестве примера. 7, мы докажем это exp.tr • exp, y = exp (* -} — y). также ср-я, я L-1 + 2GG3! ср. L-I, L la f, Где о (это) li * 1-1 2 л \ ; 1 ч + m и, следовательно, o (A) —0——0. так опыт х exp (x 4 * A) -expP £ _ exp / t— 1 -Sar L. (3) если h равно 0, или ^ -exp l; = exp lg. В частности, мы доказали, что exp: непрерывная функция. . в DY D DT против X-I-г I — J т ‘ дх И если вы определите логарифмическую функцию как инверсию экспоненциальной функции, вы достигнете отправной точки рассмотрения в начале главы. Но мы можем сделать разные выводы.
Есть много способов продолжить обсуждение. предположение Обратите внимание, что ^ = exp.t и exp 0 = 1 Людмила Фирмаль
| Ряд для арктангенса | Аналитическая теория тригонометрических функций |
| Биномиальный ряд | Функции комплексного переменного |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Из уравнения (2), если η является положительным целым числом, (Exp x) n = exp n v, (exp 1) n = exp n ~ T Если х является положительным рациональным числом, / т / 1 В м Exp-j = exp /// = (exp I) м Следовательно, exp- равно положительному значению (exp ) mn. Эта часть Результат может быть расширен до отрицательных рациональных значений х с помощью уравнения exp.vexp (-l *) — 1 и, следовательно, для всех рациональных значений x эксп. V = (exp 1) * = exp, где e = exp 1 = 1 + 1 + 1 + 1 + ….
Пример. Исследуйте бинарные последовательности аналогичным образом , + (?) * + (£) * • + … = F (a., X-), Где -1 <n * <1 f (m, x) f (m \ x) = f (m + /// ‘, l) (См. Пример LXXXI b).
Наконец, определите необоснованный .v e * как exp l:. Логарифм определяется как обратная функция. Людмила Фирмаль
