Оглавление:


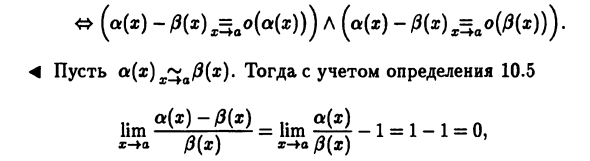

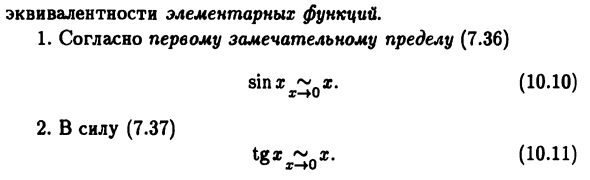

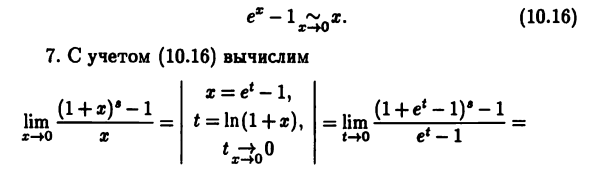

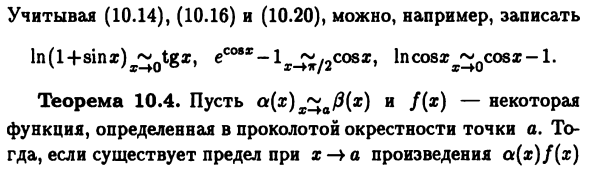


Эквивалентные бесконечно малые функции
- Особое место с той же функцией заказа в БМ Приложение будет занимать эквивалентную функцию b.m. Определение 10.5. B.M. x → a, функция a (x) и (3 (x) называется эквивалентным x- \ a, a (x) x к a (3 (x), предел отношения как x- »a Единица или гм = л. (U.8) Эквивалентное свойство работает симметрично, Поскольку lim / 3 (x) / a (x) = 1 продолжается из (10.8), Переход характеристик эквивалентности И *) L L *)) L («) LL ()) = , < (*) * ЗЛ (*) (10-9) Непосредственно следует (10.8) — (10.2). Записи вида a (x) x ~ aP (x) иногда называют Асимптотические уравнения функций a (x) и / 3 (x) в окрестности Пункт а.
Но обычно пишут слева Исследуемая функция и простая функция справа Или более исследованная функция, в этом случае они говорят Установлено асимптотическое поведение изучаемых в окрестности функций Даны баллы. Теорема 10.2. Как х- * функции для двух БМ a (x) и / 3 (x) эквивалентны x- \ a. Разница a (x) — / 3 (x) должна быть b.m. более Более высокий порядок по сравнению с каждым из них, т.е. * (A (x) — ««) d.o (b (.))) ((Φ) -P (x) x = через {P ())) Допустим, < (x) x ~ aP (x). Затем, учитывая определение 10.5 > 0 (x) И согласно определению 10.2, a (x) -fi (x) x = ao (fi (x)). Аналогично, мы можем доказать, что a (x) -0 (x) x = ao (a (x)).
Это асимптотическое уравнение можно прочитать Слева направо, справа налево. Людмила Фирмаль
И наоборот, если a (x) -P (x) x = ao (p (x)) Определение 10.2, мы имеем ..a (x) -0 (x) ..a (x), ..a (x) = lim v ‘, v; = Isht ^ -1 и lim-r} — (= l, Это означает <* (x) x для aP (x) по определению 10.5. от Предположение a (x) -β (x) a = ao (a (x)) одинаково Результат. ► Теорема 10.3. Veri B.M. x → a, функция a (x) и / 3 (x) эквивалентно x- \ a, а функция π (ξ) о Проколотая окрестность U (r) m отличается a и как t- *, если T имеет тенденцию быть комплексной функцией a (x (t)) И P (x (t)) эквивалентно t- * r. <На самом деле, согласно (7.33) и условиям этой теоремы, Рассмотрим комплексную функцию F (t) = a (x (t)) / fl (x (t)) (10.8) Есть ограничения По определению 10,5 означает «(» Эта теорема позволяет использовать подстановку переменных.
Функция при установлении эквивалентности. принять Внимание (10.8), установить некоторые основные отношения Эквивалентность основных функций. 1. Согласно первому значительному ограничению (7.36) ^ о * (10.10) 2. Согласно (7.37) , (10.11) 3. Функция x (£) = arcsin £ непрерывна в точке t = 0 (см. 9.6). Следовательно, lim arcsin t = arcsin 0 = 0 согласно (9.1). Согласно (10.10) И теорема 10.3 т = грех (дуги т) ~ дуги, или Обозначение аргумента с x> арксин х х ~ 0 я «(10.12) 4. Из непрерывности функции x (t) = arctgt в точке t = 0 (См. 0.5). Следуйте lim arctgt = arctgO = 0. Тогда из (10.11) Теорема 10.3 t = tgforctgt) ^ arctgf или указать аргумент через х «Ctg * ^ *. (10.13) 5.
- На основании второго существенного ограничения, Как и lim (l- | -x) 1 / r = e. Функция В Учитывая точку y = e, (9.12) х-ю х ИЛЬ loga (l + x) = (ln (l +: c)) / lna, поэтому согласно (10.14) 6. Из-за непрерывности функции x (t) = ex-1 в точке t = Q (см. 9.5) lim (e * -1) = 0. Согласно (10.14) Вернитесь к ln (l-he * -1) £ dv * -1 или t q * e * -1 Если аргумент представлен x, это выглядит так э’л ^ *. (10.16) 7. Рассчитать с учетом (10.16) х = е% -1, ободок И? — + 0 = Оправа «Т е е * -1
= Тонкий обод -; — = s • 1 • 1 = s. В результате (1 + x) n-l ^ q ^ ss или s∈R \ {0} -, (10.17) Особенно, когда s = 1/2 Vl + x-1 до nx / 2 Считается из полученного соотношения (10.10) — (10.17) Переход эквивалентности (10.9) продолжается -. (10.18) Согласно теореме 10.3, в этой цепочке x- * 0 b.m эквивалентный аргумент функции x сам , а limz (t) = 0. В В частности, если а> 0, ax-1 = (elne) x-1 = ex [pa-1 to xa. Например, (10.14) x-t-1 и t- »1 ln (l-ft-1) ^ -1. так Инна, (10.19) -l. (10.20) С учетом (10.14), (10.16) и (10.20), например, ln (l + 8ina?) ^ 0tg «, Теорема 10.4. <* (X) x ~ a / 3 (x) и f (x)
Некоторые могут быть ненулевыми функциями о В окрестности U (r) точки m делается отверстие Людмила Фирмаль
Функция, определенная в проколотой окрестности a. Далее, если есть ограничение на s- »a произведения a (x) f (x) (или частное f (x) / a (x)), оно изменится, даже если a (x) будет заменено на не быть. Функция f (x) эквивалентна x- + a b.m, или (IHm / («)» («) = b) A (o («), ~ ./> (*)) = * => 3 iim / (xiXx) = b, (10.21) (Lim 44 = b) A (<* (*) — / * (*)) = ^ 3 Um 44 = 6. (10.22) x * aa (x)) \ v ‘* -> a ^ v V xi »/? (X) V ‘ <На самом деле, учитывая (10.8) и (7.23) lim f (x) P (x) = lim = Оправа ха ) .. a (a) / (g) r a (x) v f (x) -f = Km ;;: = км до -r # «m = -7-7 = r / () .. a («) / (g) r a (x) v f (x) lim ^ 7-f = Km,;,;: = км ~ -r # «m = -7-7 = 1-6 = 6.► /? () ^ () () () J) Из этой теоремы легко использовать (10.18) Правило: x-> a для функции ограничения отношения Предельная функция с отношениями, эквивалентными тем в x-ta b.m. Пример 10.4 с учетом (10.18) .. Incosa; .. cosa? -l lim —5—- = км = — = 1 хл .. -2sin2 (a: / 2) ol. (Х / 2) 2 1 = lim 5 ^ — ^ = -2 lim 1 ~ V «= -» • x2 x-fO x2 2
Смотрите также:
| О вычислении нуля функции, непрерывной на отрезке | Главная часть бесконечно малой функции |
| Сравнение бесконечно малых функций | Сравнение бесконечно больших функций |
