Оглавление:
Эллипс, гипербола и парабола относятся к кривым второго порядка, расположенным на плоскости 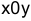 . Канонические (наиболее простые) уравнения этих кривых соответствуют определённому положению их относительно осей координат.
. Канонические (наиболее простые) уравнения этих кривых соответствуют определённому положению их относительно осей координат.
Эллипс описывается каноническим уравнением:

Эллипс симметричен относительно осей координат и лежит внутри прямоугольника 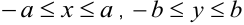 (рисунок 3.2). Точки
(рисунок 3.2). Точки 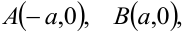
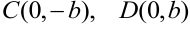 называются вершинами эллипса, т.
называются вершинами эллипса, т. 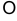 — центр эллипса.
— центр эллипса.
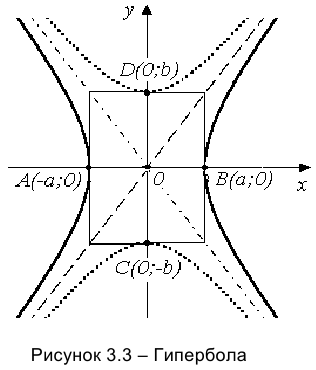
Гипербола описывается каноническим уравнением:

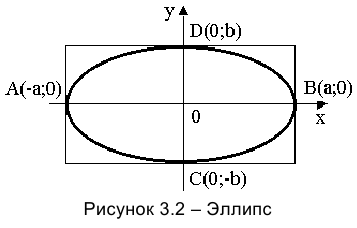
Гипербола симметрична относительно осей координат и лежит вне прямоугольника 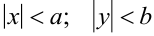 внутри двух углов, образованных его диагоналями (рисунок 3.3). Точки
внутри двух углов, образованных его диагоналями (рисунок 3.3). Точки 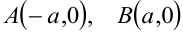 называются вершинами гиперболы, отрезок
называются вершинами гиперболы, отрезок 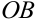 — действительная полуось,
— действительная полуось, 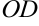 — мнимая полуось. Прямые, проходящие по диагонали осевого прямоугольника, называются асимптотами гиперболы.
— мнимая полуось. Прямые, проходящие по диагонали осевого прямоугольника, называются асимптотами гиперболы.
В том же осевом прямоугольнике можно построить гиперболу, вершины которой — 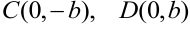 . Такую гиперболу называют сопряженной гиперболе (3.19). На рисунке 3.3 точечной линией показана сопряжённая гипербола, уравнение которой:
. Такую гиперболу называют сопряженной гиперболе (3.19). На рисунке 3.3 точечной линией показана сопряжённая гипербола, уравнение которой:

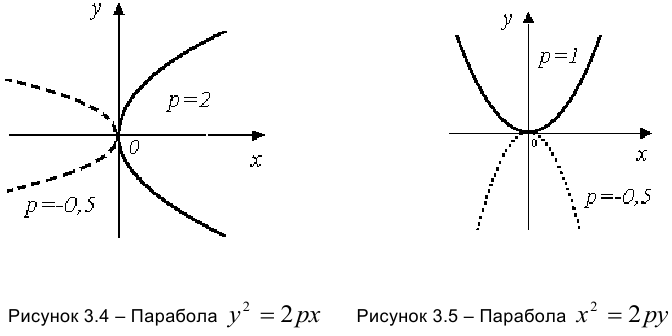
Параболы с каноническими уравнениями:

симметричны относительно осей 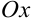 (3.21) и
(3.21) и 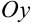 (3.22). Начало координат является вершиной обеих парабол.
(3.22). Начало координат является вершиной обеих парабол.
Если параметр 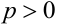 , ветви парабол направлены в сторону положительного направления оси, если
, ветви парабол направлены в сторону положительного направления оси, если 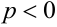 — в обратную сторону (рисунки 3.4 и 3.5).
— в обратную сторону (рисунки 3.4 и 3.5).
Если эллипс, гипербола или парабола смещены параллельным переносом так, что центр осевого прямоугольника эллипса и гиперболы или вершина параболы лежит в точке с координатами 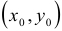 , то уравнения этих кривых преобразуются к виду:
, то уравнения этих кривых преобразуются к виду:
эллипс: 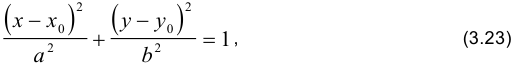
гипербола: 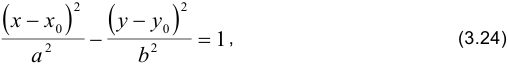
парабола: 

Пример выполнения задания
Пример:
Даны два уравнения кривых второго порядка: Г1: 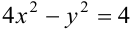 ; Г2:
; Г2: 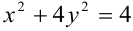 .
.
Требуется: привести их к каноническому виду, определить тип и построить эти кривые.
Решение:
Уравнение Г1 разделим на 4 и получим: 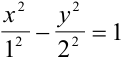 .
.
Уравнение имеет вид (3.19), следовательно, это гипербола, причём 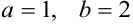 . Её построение см. рисунок 3.3.
. Её построение см. рисунок 3.3.
Уравнение Г2 разделим на 4 и получим уравнение эллипса:
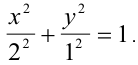
Построение эллипса см. рисунок 3.2.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Уравнения прямой линии на плоскости |
| Уравнения плоскости в пространстве |
| Предел бесконечной числовой последовательности |
| Предел функции при x>a |
