Геометрическая прогрессия с примерами решения

Геометрическая прогрессия

а) Геометрическая прогрессия — последовательность 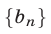, определяемая рекуррентной формулой

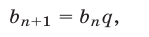
где 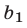и 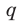— заданные числа, отличные от нуля; число 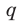называется знаменателем геометрической прогрессии.

б) Для n-го члена геометрической прогрессии справедлива формула

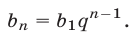
в) Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению его соседних членов, т. е. при 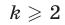справедливо равенство

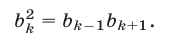
Если 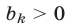при всех 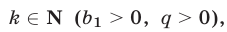то

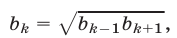
т. е. каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому его соседних членов.

г) Если рассматривается совокупность первых n членов геометрической прогрессии, т.е. числа 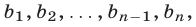то произведение каждой пары членов, равноотстоящих от крайних членов этой совокупности, равно произведению крайних членов, т. е. при 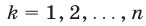справедливо равенство

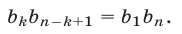
д) Сумма первых n членов геометрической прогрессии выражается формулой

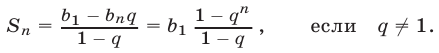
Пример №27.

Найти первый член и знаменатель геометрической прогрессии, если сумма ее первого и третьего членов равна 35, а сумма первых пяти членов в 49 раз больше суммы их обратных величин.

Решение:

По условиям задачи

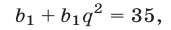
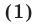
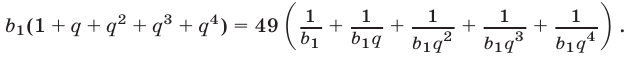
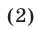
Так как 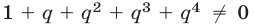(иначе задача теряет смысл), то равенство (2), в котором правая часть равна 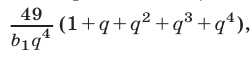можно записать в виде

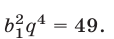
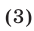
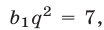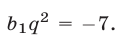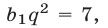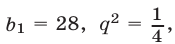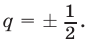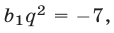Из (3) следует, что либо либо Если то из (1) находим откуда Еслито 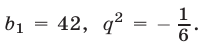В этом случае теряет смысл второе условие задачи.

Ответ.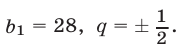

Пример №28.

Пусть 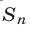— сумма первых n членов геометрической прогрессии. Доказать, что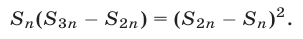

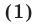
Доказательство. Пусть 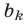— k-й член, q — знаменатель геометрической прогрессии. Тогда

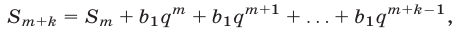
откуда

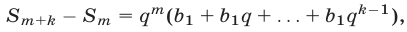
или

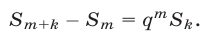
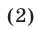
Полагая в (2) сначала 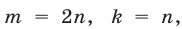а затем 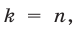получаем

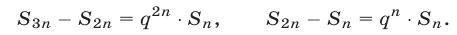
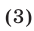
Из равенств (3) следует равенство (1).

Пример №29.

Найти числа x,y,z,t, если они являются последовательными членами арифметической прогрессии, а числа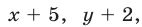 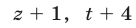являются последовательными членами геометрической прогрессии.

Решение:

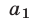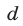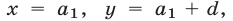
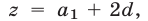
Пусть — первый член, — разность арифметической прогрессии. Тогда 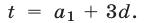По свойству геометрической прогрессии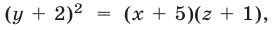 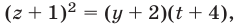т.е.

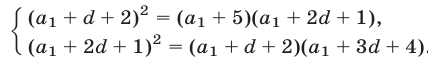
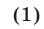
Систему (1) можно преобразовать к следующему виду:

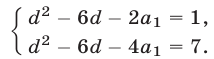
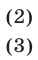
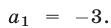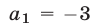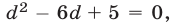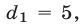
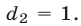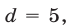Вычитая из (2) уравнение (3), находим Подставляя в уравнение (2), получаем откуда Если то 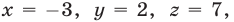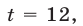а если 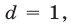то 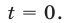Значение 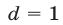следует отбросить, так как числа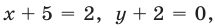 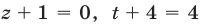не образуют геометрическую прогрессию.

Ответ: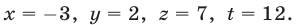

Пример №30.

Найти числа х, у, z и t, если они обладают следующими свойствами:

числа х, у и z образуют в указанном порядке геометрическую прогрессию;

числа у, z и t образуют в указанном порядке арифметическую прогрессию;

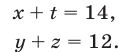
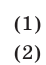
Решение:

По свойствам прогрессий

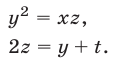
Будем решать систему (1)-(4) методом исключения неизвестных. Из (1) и (4) следует, что

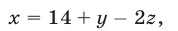
а из (2) находим

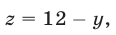
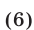
откуда получаем

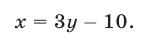
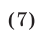
Подставляя выражения для х и z из (6) и (7) в уравнение (3), приходим к уравнению

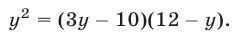
Это уравнение можно записать в виде 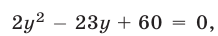откуда 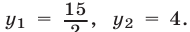Соответствующие значения z, х и t найдем из уравнений (6), (7) и (1).

Ответ.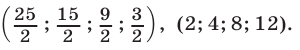

Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:

Решение задач по математике

Возможно вам будут полезны эти страницы:

Логарифмы примеры с решением

Числовая последовательность и арифметическая прогрессия с примерами решения

Предел последовательности с примером решения

Бесконечно убывающая геометрическая прогрессия с примерами решения