Геометрические характеристики плоских сечений
Как было показано выше, при деформации растяжения и сжатия площадь поперечного сечения полностью характеризовала прочность и жесткость детали. Однако при деформации изгиба и кручения прочность и жесткость характеризуются не только размерами сечения, но и его формой. К числу геометрических характеристик сечения, учитывающих оба указанных фактора, относятся статические моменты, моменты инерции, моменты сопротивления.
Статические моменты площадей. Координаты 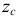 и
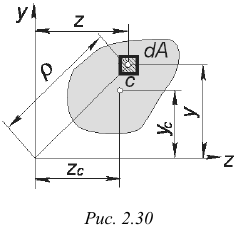
и 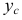 центра тяжести плоской фигуры (рис. 2.30) определяются, как известно из общей механики, формулами
центра тяжести плоской фигуры (рис. 2.30) определяются, как известно из общей механики, формулами
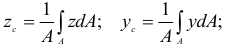
где 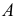 — площадь всей фигуры;
— площадь всей фигуры; 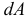 -элемент площади.
-элемент площади.
Интегралы вида 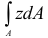 и
и 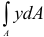 называют статическими моментами фигуры относительно осей
называют статическими моментами фигуры относительно осей 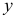 и
и 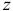 и обозначают соответственно через
и обозначают соответственно через 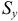 и
и 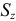 .
.
Таким образом, на основании (2.37) имеем
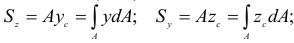
Из формул (2.37) и (2.38) следует, что статический момент площади фигуры относительно какой-либо оси равен сумме статических моментов частей, из которых состоит фигура, относительно той же оси.
Оси, проходящие через центр тяжести фигуры, называют центральными осями. Статические моменты площадей относительно центральных осей равны нулю, так как 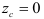 или
или 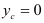 .
.
Моменты инерции плоских сечений. Различают осевые, полярные и центробежные моменты инерции.
Осевым моментом инерции сечения называют взятую по всей площади сечения сумму произведений элементарных площадок на квадраты их расстояний до соответствующей оси. Обозначая.моменты инерции относительно осей 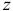 и
и 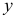 соответственно через
соответственно через 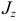 и
и 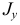 (рис. 2.30), имеем
(рис. 2.30), имеем
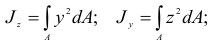
Полярным моментом инерции (моментом инерции относительно полюса) называют взятую по всей площади сечения сумму произведений элементарных площадок на квадраты их расстояний до данного полюса:
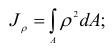
Центробежным моментом инерции сечения называют взятую по всей площади сечения сумму произведений элементарных площадок на обе координаты в данной прямоугольной системе осей. Обозначая центробежный момент инерции через 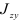 , имеем
, имеем
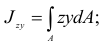
Моменты инерции измеряют в единицах длины в четвертой степени, чаще всего в 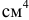 .
.
Из приведенных определений следует, что момент инерции сложной фигуры равен сумме моментов инерции ее частей.
Рассмотрим некоторые свойства моментов инерции.
- Момент инерции относительно полюса, являющегося началом прямоугольной системы координат, равен сумме моментов инерции относительно осей данной системы.
Из рис. 2.30 следует:
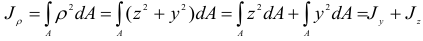
Если
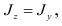
то
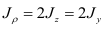
- Момент инерции сечения относительно какой-либо оси равен моменту инерции этого сечения относительно центральной оси, параллельной данной, сложенному с произведением площади сечения на квадрат расстояния между осями.
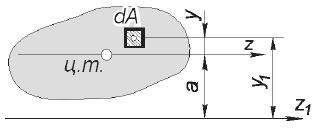
Из рис. 2.31 следует, что
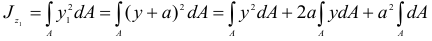
Но
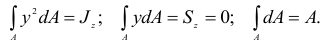
Таким образом,
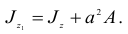
Рассмотрим понятие о главных осях инерции. Две взаимно перпендикулярные оси с началом в данной точке, для которых центробежный момент инерции плоской фигуры равен нулю, называют главными осями инерции фигуры в этой точке. Главные оси инерции в центре тяжести фигуры называют главными центральными осями инерции.
Легко показать, что в том случае, когда фигура имеет хотя бы одну ось симметрии, эта ось является одной из главных центральных осей инерции, а другая проходит через центр тяжести фигуры перпендикулярно первой. Если хотя бы одна из двух взаимно перпендикулярных осей, проходящих через центр тяжести сечения, является осью симметрии, то такие оси являются главными центральными осями инерции. Для таких сечений, как круг и кольцо любые две взаимно перпендикулярные центральные оси являются главными осями инерции.
В общем случае главные центральные оси инерции фигуры могут быть найдены, если известны ее центробежный 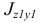 и осевые
и осевые 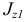 и
и 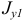 моменты инерции относительно произвольно расположенных центральных осей
моменты инерции относительно произвольно расположенных центральных осей 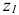 и
и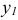 .
.
Для этого систему осей 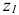 и
и 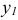 необходимо повернуть на угол а, определяемый из соотношения
необходимо повернуть на угол а, определяемый из соотношения
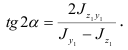
Моменты инерции относительно главных центральных осей инерции называют главными моментами инерции: они обладают тем свойством, что один из них имеет максимальное, а другой минимальное значение по сравнению с моментами инерции относительно остальных центральных осей. Главные моменты инерции
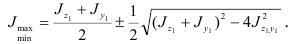
Значения моментов инерции простейших фигур, а также прокатных профилей можно найти в технических справочниках или вычислить по приведенным выше формулам.
Определим величины моментов инерции наиболее распространенных плоских сечений, встречающихся при расчетах и конструировании деталей механизмов.
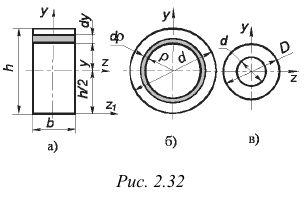
Прямоугольник высотой 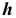 и шириной
и шириной 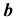 (рис. 2.32, а). Выделим в прямоугольнике элементарную полоску высотой
(рис. 2.32, а). Выделим в прямоугольнике элементарную полоску высотой 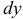 и шириной
и шириной 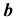 . Полоска отстоит от центральной оси
. Полоска отстоит от центральной оси 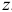 , параллельной основанию на расстоянии
, параллельной основанию на расстоянии 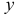 . При этом
. При этом 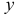 изменяется в пределах
изменяется в пределах 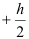 до
до 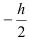 .
.
На основании формулы (2.39) имеем
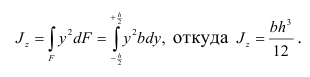
Аналогично
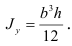
Для того же прямоугольника момент инерции относительно оси, проходящей через основание,
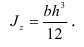
Круг диаметром 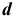 (рис. 2.32, б). Выделим в круге элементарную площадь в виде кольца радиусом
(рис. 2.32, б). Выделим в круге элементарную площадь в виде кольца радиусом 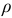 и шириной
и шириной 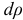 . Площадь кольца
. Площадь кольца
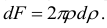
Применив формулу (2.42), получим величину полярного момента инерции относительно центра круга:
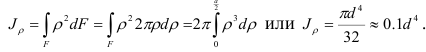
Круговое кольцо с наружным диаметром 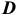 и внутренним
и внутренним 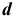 .
.
В данном случае полярный момент инерции может быть получен как разность полярных моментов инерции большого и малого круга (рис. 2.32, в). С учетом уравнений (2.48) имеем
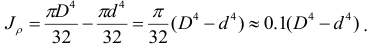
Обозначив 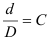 , после подстановки в выражение (2.49), получим
, после подстановки в выражение (2.49), получим
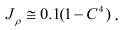
Исходя из соотношения (2.42, а), находим осевые моменты инерции круга и кругового кольца
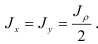
Для круга с учетом соотношения (2.42)
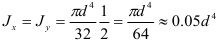
Для кольца, принимая во внимание выражения (2.49) и (2.50),
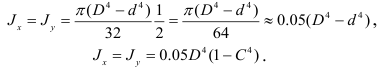
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Типы опор и определение опорных реакций. Общие понятия |
| Поперечная сила и изгибающий момент |
| Чистый сдвиг и его особенности |
| Напряжения при изгибе. Расчеты на прочность |
