Оглавление:
Площадь криволинейной трапеции
Пусть на отрезке 
задана непрерывная функция 
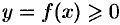. Фигура, ограниченная сверху графиком функции 
, снизу — осью 
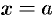, сбоку — прямыми 
и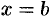 
, называется криволинейной трапецией. Найдем площадь этой трапеции.
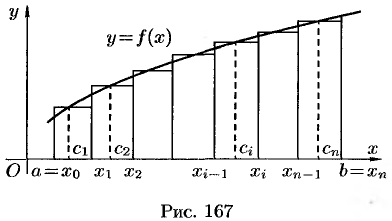
Для этого отрезок точками 
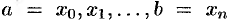
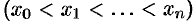разобьем на 
частичных отрезков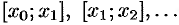 
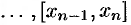(см. рис. 167). В каждом частичном отрезке 
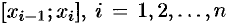возьмем произвольную точку 
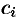и вычислим значение функции в ней, т. е. 
.
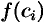Умножим значением функции 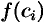на длину 
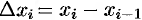соответствующего частичного отрезка. Произведение 
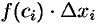равно площади прямоугольника с основанием 
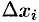и высотой 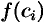. Сумма всех таких произведений
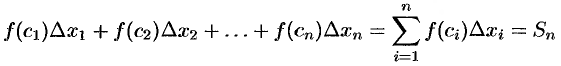
равна площади ступенчатой фигуры и приближенно равна площади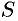 
криволинейной трапеции:
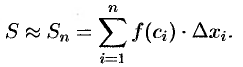
С уменьшением всех величин 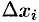точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади 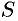криволинейной трапеции принимается предел 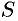, к которому стремится площадь ступенчатой фигуры 
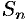, когда неограниченно возрастает так, что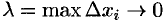 
:
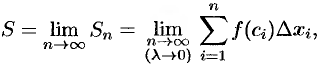то есть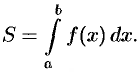 
fl у
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
В этом состоит геометрический смысл определенного интеграла.
Работа переменной силы
Пусть материальная точка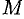 
перемещается под действием силы 
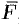, направленной вдоль оси 
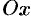и имеющей переменную величину 
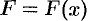, где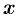 
— абсцисса движущейся точки .
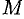Найдем работу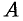 
силы 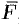по перемещению точки 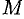вдоль оси 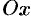из точки 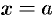в точку (
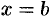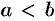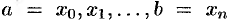
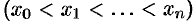). Для этого отрезок точками разобьем на частичных отрезков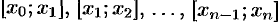 
. Сила, действующая на отрезке 
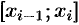, меняется от точки к точке. Но если длина отрезка 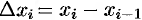достаточно мала, то сила 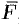на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции 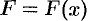в произвольно выбранной точке 
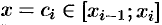. Поэтому работа, совершенная этой силой на отрезке 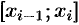, равна произведению 
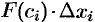. (Как работа постоянной силы 
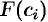на участке .)
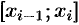Приближенное значение работ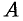ы силы 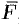на всем отрезке есть
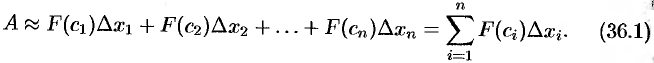
Это приближенное равенство тем точнее, чем меньше длина 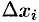. Поэтому за точное значение работы 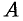принимается предел суммы (36.1). при условии, что наибольшая длина 
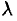частичных отрезков стремится к нулю:
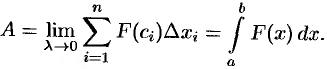
Итак, работа переменной силы 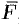, величина которой есть непрерывная функция 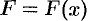, действующей на отрезке , равна определенному интегралу от величины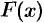 
силы, взятому по отрезку .
В этом состоит физический смысл определенного интеграла.
Аналогично можно показать, что путь 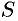, пройденный точкой за промежуток времени от 
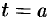до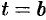 
, равен определенному интегралу от скорости 
:
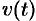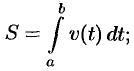
масса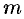 
неоднородного стержня па отрезке равна определенному интегралу от плотности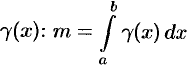 
.
Формула Ньютона-Лейбница
Пусть функция интегрируема на отрезке .
Теорема 37.1. Если функция непрерывна на отрезке и 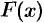— какая-либо ее первообразная на 
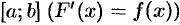, то имеет место формула
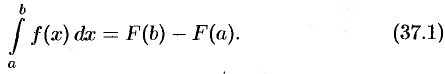
Разобьем отрезок точками 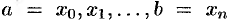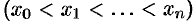на частичных отрезков 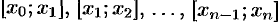, как это показано на рис. 168.
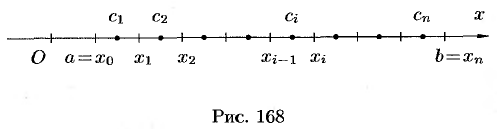
Рассмотрим тождество
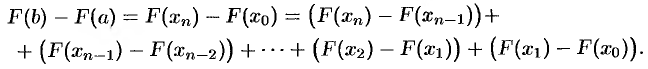
Преобразуем каждую разность в скобках по формуле Лагранжа
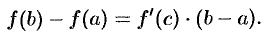
Получим
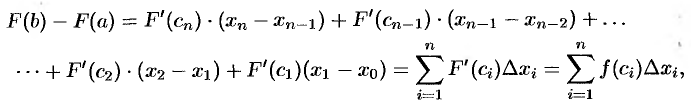
т.е.
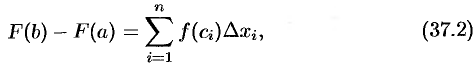
где 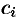есть некоторая точка интервала 
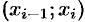. Так как функция непрерывна на , то она интегрируема на . Поэтому существует предел интегральной суммы, равный определенному интегралу от 
на .
Переходя в равенстве (37.2) к пределу при 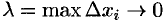, получаем
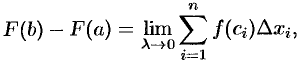
т. е.
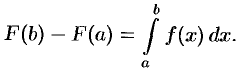
Равенство (37.1) называется формулой Ньютона-Лейбница. Если ввести обозначение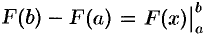 
, то формулу Ньютона-Лейбница (37.1) можно переписать так:
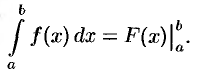
Формула Ньютона-Лейбница даст удобный способ вычисления определенного интеграла. Чтобы вычислить определенный интеграл от непрерывной функции на отрезке , надо найти ее первообразную функцию 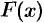и взять разность 
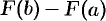значений этой первообразной на концах отрезка .
Например,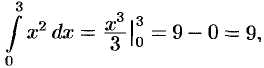 
а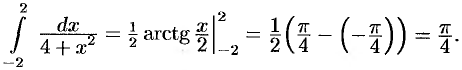 
Пример №37.1.
Вычислить интеграл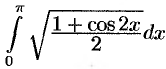 
.
Решение:
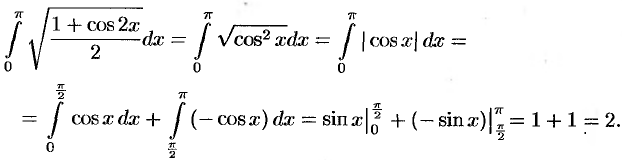
Дополнительный пример №37.2.
Дополнительная лекция: Работа переменной силы в определённом интеграле
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| «Берущиеся» и «Неберущиеся» интегралы |
| Определенный интеграл как предел интегральной суммы |
| Основные свойства определенного интеграла |
| Вычисления определенного интеграла |
