Группа подстановок

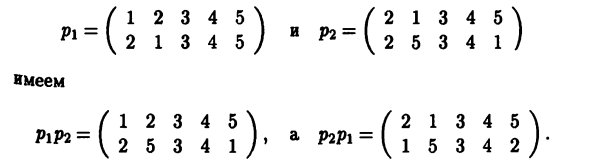
Группа подстановок

• Самооценка один на один (или Преобразование) 7V конечного множества = (1, 2, 3, …, n) first n Вызывается n подстановка натуральных чисел (или Порядок замены). Замена обычно пишется как заключенный Две строки чисел в скобках. Например, взаимное Четкое соответствие заданных натуральных чисел 1, 2 и 3 многие {(2,3), (1,2), (3,1)} Написано как заказанная пара, замена р. степень «2 3 2 1 ■ ( 2 становится 3, 1 становится 2, а 3 становится 1. Сортировка не меняется Разместите заказанные пары, такая же замена

Представлено в нескольких формах: I 2) ITD- Предпочтительная запись, топ номер Ряды расположены в естественном порядке. тогда замена n-го порядка принимает форму / 1 2 … n \ р = я , , 1 (4,19) Где * b% 2y …, rn частично Первые n натуральных чисел в определенном порядке. Все изменения Место определяет новую альтернативу и общее Перестановка первых n элементов множества N в нижнем ряду (4.19). подстановка идентификаторов n-го порядка Вы можете конвертировать каждое число в себя и написать: / 1 2 … n \ VI 2 … n) ‘ (4,20) n-я перестановка p-конфигурация jp2 ° Pi

Количество перестановок n-го порядка равно числу n! Он совпадает. Людмила Фирмаль

Называется n-ая перестановка p = P \ P2. Результат выполнения последовательного отображения. Сначала запросите пи, затем pg-configure Перестановки написаны в виде продуктов, В обратном порядке, p \ P2ΦpiP \ • Например, Посмотрите вверх / 1 2 3 4 5 \ / 2 1 3 4 5 \ P1 = \ 2 1 3 4 b) и P2 = [2 5 s 4 1) Очевидно, что если p является заменой n-го порядка, P * n = epr = P, Другими словами, эп действует как нейтральный элемент Юридическая настройка карт. Оставьте строку замены p Поменяйте на (4.19) чтобы получить замену -1 _ («1 * 2 ••• in \ P «V 1 2 … n) y Реверс перестановки р, со свойствами То есть р ~ 1 действует как симметричный элемент р По поводу закона композиции картографирования.

Вот так Установите n P! перестановка n-порядка Мультипликативные группы, связанные с этим (см. Таблицу 4.1) В этом случае закон, который играет роль умножения Закон (ассоциативный, но не коммутативный). многие P называется группой замещения n-го порядка. Первая строка при написании формы (4.19) Без изменений, замена n-го порядка может быть указана только вторым заказом. линия: То есть перестановка первых n элементов множества N При такой замене меняйте любые два числа (не Неизбежно встаньте рядом), а остальное оставьте сами После размещения вы получите новую перестановку. Это Преобразование называется перестановкой подстановки.

• Два числа Чем меньше из них образует инверсию перестановки Большой (или, как говорится, Меньше перестановок, чем раньше). перераспределение Вызывается, даже если общее количество переворотов строки четное. Странно — в противном случае. Рассчитать общее количество нескольких инверсий Каждая перестановка из n элементов сравнивается последовательно Элемент, начинающийся с первого элемента слева, за которым следуют все элементы, Определите количество маленьких чисел справа. Это указывает на количество инверсий для этого элемента. Я получил это Добавлены номера метода n-1. Пример 4.12. а.

Перестановка (1, 2, …, n) Любое п. Потому что количество инверсий равно нулю. б. Перестановка (7, 4, 5, 1, 3, 6, 2) содержит 14 инверсий (6 + 3 + 3 + 0 + 1 + 1), поэтому даже. с. 17 для перестановок (3, 8, 5, 2, 4, 6, 9, 7, 1) Это странно, потому что это инвертировано (2 + 6 + 3 + 1 + 1 + 1 + 2 + 1). Теорема 4.7. Перестановка меняет паритет Перестановка. <Во-первых, заменяемое число я И J выстроились в очередь. Это транспонировать. Обе перестановки соответственно Обратная величина чисел r и j равна Останется в этом месте.

Перестановка источников и перестановка, Форма, полученная транспозицией Точка заменяет числа, которые не имеют никакого эффекта Людмила Фирмаль

Оригинальные номера r и j Перестановка не образует инверсию, но после транспозиции Один новый флип происходит. Эти же номера оригинальных Перестановка форм инверсии и после транспозиции Исчезает, т.е. общее количество инверсий будет 1 Поменьше. В обоих случаях перестановочная четность меняется. Далее между заменяемыми числами r и j m чисел в {me N). Начальная перестановка Имеет форму .., 2, K \ a2i •••! * t> J «… j.

Вы можете переставить первые слова i и j со следующими последствиями: Выполните 2tp +1 шаги, чтобы изменить расположение соседних номеров (Перемещает r c ^ i, переставляет r вместо & i, c k2, И т.д., пока m шагов r не пройдут kt и не станут близки поменяйте местами r и j с j \ и, наконец, t Изменить порядок j с помощью ct fcm_i и т. д. Тогда j заменит r, числа & i, & 2 «…, CT сохраняет местоположение). Кроме того, перестановка четность Нечетное количество изменений (2ga + 1) раз. Следовательно, перестановка (4.21) и ••• »3> * 1» * 2> ••• »

Имеет противоположное соотношение. ► Рассмотрим обозначение подстановки (4.19). перестановка В верхнем и нижнем рядах есть одно из следующих То же или противоположное соотношение. Переход на любой Различные записи могут быть сделаны последовательно Выполните некоторое перемещение в верхнем ряду, Транспонирование соответствует нижнему ряду. но Выполните одну транспонирование и одну в верхнем ряду (4.19) Транспонировать соответствующий элемент в нижнем ряду, Изменить соотношение обеих перестановок одновременно, Следовательно, он сохраняет паритет случайно или наоборот.

Для любой записи с заменой четности Верхний ряд соответствует нижнему ряду, Напротив. Определение 4.10. Замена называется даже когда Перестановки обеих строк имеют одинаковую четность, Странно — противоположный случай. Подмена идентичности (4.20) Четность и четность перестановок определены в формате (4.19), Соответствует четности перестановки нижнего ряда. Вышесказанное можно обобщить по отношению друг к другу Очистить отображение (преобразование) к себе Конечный набор £ «= {ai, 02, …, an} (Не обязательно номер 4) При нумерации элементов Первые n натуральных чисел.

Пример 4.13. n = 3, a1 = A, a2 = B, az = = C — вершина равностороннего треугольника (рис. 4.5). Установите P из -n! = 3! = 6 Посмотрите вверх / 1 2 3 л Где, «2> * с 3 натуральных в каком-то порядке Числа 1, 2 и 3 обозначают группы на рисунке 1. 4.5 Симметрия этого треугольника, т.е. Такое смещение треугольника в такой плоскости Подходим себя Для замены личности е ii = 1,% 2 = 2, r’z = 3 оставляет треугольник на месте. в ii = 2, r’r = 3, «s = 1 и ii = 3, r # 2 = 1, a’z = 2 (четные перестановки ай /? ) Треугольник вращается против часовой стрелки Стрелки, связанные с каждой точкой O под углом a = = 2тг / 3 и / 3 = 4тг / 3 (см. Рис. 4.5). Если i’i = 1, r’2 = 3, is = 2 (Нечетная перестановка q) треугольник вращается Ось симметрии ОА.

Ось симметрии ОВ и ОС дает нечетные перестановки r и s соответственно. 4 = 3, 2 = 2, r3 = 1 и r * 1 = 2, r2 = 1, r’z = 3. Произведение piP2 любой из этих перестановок также Определите одну из операций, которая соединяет треугольники (например, qr = (3). Левый столбец и верхний ряд таблицы. 4.2 Размещение Обозначения перестановок p1 и p2, а также Оставшееся место — произведение p \ p2 этих перестановок. е но P Я г 8 но 0 е 8 Я г P е но г s Я Я г 8 е но P г 8 Я р е но 8 Я г но P е 170 4. Основной закон композиции Каждая строка и каждый столбец таблицы. 4,2 Существует такая же перестановка e. Для всех операций Для симметричной (или обратной) и вращательной работы

Относительно оси симметрии (и, конечно, Та же операция) Противоположна сама операция. Стол асимметричный Лицо. По главной диагонали (Пройти верхний левый И нижний правый элемент) Показывает снова подмена Некоммутативная. Набор P считается Перестановка также называется Симметричная группа фигур (в данном случае Равносторонний треугольник). Точно так же вы можете построить группу Симметрия других геометрических объектов Целое все преобразования метрического пространства,

Объедините это с собой (например, симметричная группа Квадрат, куб, тетраэдр и т. Д.). С такой позиции Б.С. в 1890 году Федоров создал правильную классификацию Прикладная система пространственных точек Кристаллографии. Исторически это было первое применение теории. Естественнонаучная группа.

Смотрите также:

Предмет математика

Законы композиции	Понятие метрического пространства
Основные алгебраические структуры	Окрестности в метрическом пространстве