Импульс силы
С понятием количества движения тесно связано но< нятие импульса силы.
Рассмотрим сначала случай, когда на точку действует постоянная по модулю и по направлению сила.
Импульсом постоянной силы за некоторый промежуток времени называется вектор, равный произведению силы 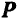 на данный промежуток времени
на данный промежуток времени 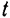 . Обозначая импульс силы через
. Обозначая импульс силы через 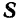 , будем иметь:
, будем иметь:
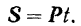
Так как время есть скалярная величина, то направление вектора 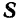 совпадает с направлением силы
совпадает с направлением силы 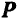 .
.
Импульс силы имеет размерность
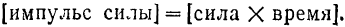
Как видим, импульс силы имеет одинаковую размерность с количеством движения.
Для перехода к определению импульса переменной силы за некоторый конечный промежуток времени 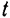 разобьем этот промежуток на бесконечно большое число бесконечно малых элементов времени. На протяжении каждого такого бесконечно малого промежутка времени силу можно считать постоянной как по модулю, так и по направлению.
разобьем этот промежуток на бесконечно большое число бесконечно малых элементов времени. На протяжении каждого такого бесконечно малого промежутка времени силу можно считать постоянной как по модулю, так и по направлению.
Импульс силы за бесконечно малый промежуток времени ее действия называется элементарным импульсом.
Обозначая элементарный импульс через 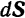 , будем иметь:
, будем иметь:
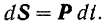
Импульс 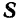 силы за некоторый конечный промежуток времени есть предел, к которому стремится геометрическая сумма элементарных импульсов силы, когда число элементарных промежутков времени, на которые разбит данный промежуток времени, неограниченно возрастает.
силы за некоторый конечный промежуток времени есть предел, к которому стремится геометрическая сумма элементарных импульсов силы, когда число элементарных промежутков времени, на которые разбит данный промежуток времени, неограниченно возрастает.
Так как элементарные импульсы силы есть векторы, то импульс силы за конечный промежуток времени равен векторному определенному интегралу от силы 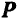 по времени
по времени 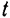 , вычисленному в пределах изменения аргумента:
, вычисленному в пределах изменения аргумента:
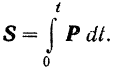
Векторный интеграл обозначается обычным образом, но надо иметь в виду, что здесь в интегральной сумме слагаемыми являются не скалярные величины, а векторы.
Импульс 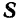 может быть вычислен при помощи метода проекций.
может быть вычислен при помощи метода проекций.
Проекция на какую-либо ось импульса 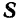 силы, действующей на точку за некоторый промежуток времени, равна импульсу проекции этой силы на ту же ось и за то же время:
силы, действующей на точку за некоторый промежуток времени, равна импульсу проекции этой силы на ту же ось и за то же время:
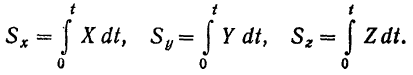
В случае постоянной силы проекции ее импульса на координатные оси:
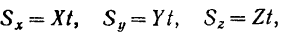
где 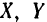 и
и 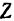 — проекции силы на соответствующие координатные оси.
— проекции силы на соответствующие координатные оси.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
