Оглавление:
С помощью тригонометрических подстановок вычисляются интегралы вида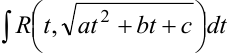 
, то есть содержащие под знаком квадратного корня квадратный трехчлен.
Путем выделения полного квадрата под знаком радикала и перехода при этом к новой переменной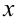 
в зависимости от знака старшего коэффициента 
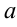и от знака дискриминанта 
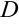подкоренного выражения возможны следующие случаи:
1) Если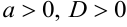 
, то интеграл преобразуется к виду 
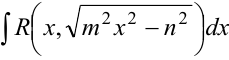. Подстановка 
.
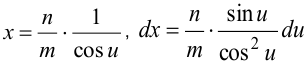2) Если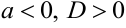 
, интеграл преобразуется к виду
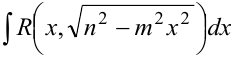. Подстановка 
.
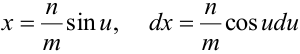3) Если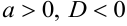 
, интеграл преобразуется к виду
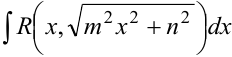. Подстановка 
.
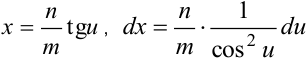Указания к выполнению задания
1) Один из способов определения интеграла по пункту а) приведен в примере 6.2 параграфа 6.2. Другой способ — нахождение неопределенного интеграла методом подстановки рассмотрен в следующем примере.
Пример №1:
Найти неопределенные интегралы методом подстановки: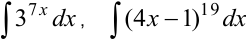 
.
Решение:
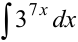. Пусть 
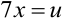, тогда 
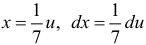. Подставим новую переменную в интеграл: 
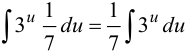. Вынесли постоянный множитель за знак интеграла и получили табличный интеграл (таблица 3, пункт 3, где 
).
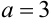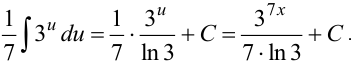
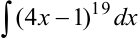. Пусть 
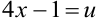. Тогда 
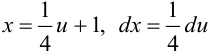. Подставим новую переменную в интеграл: 
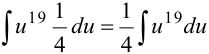. Вынесли постоянный множитель за знак интеграла и получили табличный интеграл (таблица 3, пункт 1, где 
).
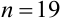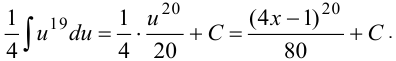
Подчеркнем, что после определения первообразной относительно новой переменной обязательно нужно вернуться к старой переменной .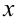
2) При решении интегралов по пункту б) применяется частный случай метода подстановки — подведение выражения под знак дифференциала.
В подынтегральном выражении нужно отыскать функцию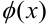 
, производная от которой 
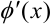также присутствует в подынтегральном выражении. Используем подстановку 
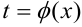, при этом 
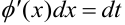. Использование приема подведения выражения под знак дифференциала рассмотрено в примерах 6.6 и 6.7 параграфа 6.5.
При решении интегралов пункта б) нужно воспользоваться таблицей производных из материала 1-го семестра. Так, очевидно, что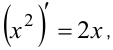 
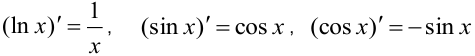и так далее. Кроме того, 
.
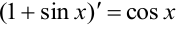3) В пункте в) задан интеграл от правильной рациональной дроби. Этот интеграл равен сумме интегралов от простейших дробей. Простейшие дроби нужно получить разложением заданной рациональной дроби. Теория вопроса описана в параграфах 6.6 — 6.8. Рассмотрим следующий пример.
Пример №2:
Найти неопределенный интеграл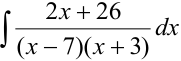 
.
Решение:
Под знаком интеграла — правильная рациональная дробь, знаменатель которой разложен на простейшие линейные множители. Каждый линейный множитель соответствует простому действительному корню знаменателя. Из параграфа 5.8: «каждому простому действительному корню соответствует простейшая дробь 1-го типа». Поэтому рациональная дробь равна сумме двух простейших дробей 1 -го типа: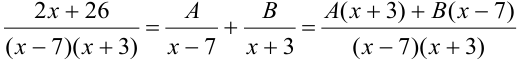 
. Коэффициенты 
, 
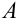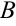— неизвестны. Чтобы их найти мы сложили две дроби, а теперь приравняем числители исходной дроби и полученной:
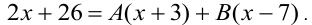
Равенство справедливо для всех значений 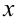. Удобно задать такие значения 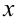, при которых выражение упрощается.
Пусть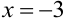 
, тогда 
.
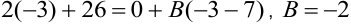Пусть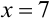 
, тогда 
.
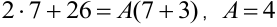Итак,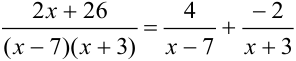 
, следовательно,
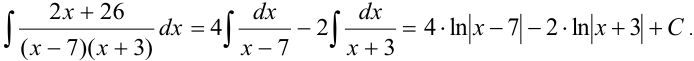
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Интегралы от иррациональных функций |
| Интегрирование тригонометрических функций |
| Задача о площади криволинейной трапеции, определение определенного интеграла |
| Все свойства определённого интеграла |
