Оглавление:






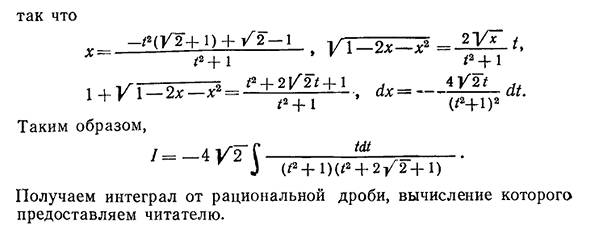

Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений
- Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений. Важную роль в обсуждении данного параграфа играют Р А С и о н л ь н а я Ф У К К и й Ву х а р г У М Е Н Т О В. определение такого признака раскрывает некоторые свойства. M n o go CHL EN o m step EN и n из двух аргументов x и y называется выражением вида RP (x, y)=a OO+^1oh+ao11/+a2oh2+ach (/- 1aogr2+… аапуп, Аю, через А1М…, AOP
показывает некоторые постоянные вещественные числа, ano, U (n-i) i, I (n-2) 2, среди таких чисел—…Если, и есть хотя бы одно число, отличное от нуля. Р А Ц и о н а л ь н о г ф Н К Ц и Е Й из д В У Х р ГУ М Е Н Т О В х н У является выражением form7?(Х, Y)= RP (x, y) Qm(x, y)’ Эти полиномы представляют собой любой полином из аргументов x и y степени n В RP(x, y) и любой полином из аргументов x и y степени
t в Qm (x, y). Если R(x,y)-рациональная функция двух аргументов x,y и■^1(0, — ^g(0, R$(t) — произвольная рациональная функция трех Людмила Фирмаль
переменных t, R[Ri(t), R2 (f)]R3 (f)(8.58) Чтобы доказать это утверждение, в результате применения его к рациональной функции、- 11 Зак 76322Ч. 8. Первичные и неопределенные интегралы С помощью операции сложения, вычитания, умножения и деления пояса t получается рациональная функция одной переменной T. В дальнейшем, чтобы доказать интегрируемость в основных функциях некоторых выражений Интеграла формулы, который учитывается в Интеграле рациональной дробис помощью специально подобранной
подстановки, в этом случае будет сказано, что интегралами учитываемых выражений являются Р А С и о н а л и * Интегрируемость основной рациональной дробной функции устанавливается в теорему 8. 5. 1°. I n t e g R I R o V i e N E K o t O R s h T R I t R I h h you Raj EN I j. будущий символ R (x, y) показывает рациональную функцию двух аргументов x и y. В этот момент докажите интегрируемость в основной функции любой функции в форме 7? (sin x, cosx). (8.59>докажите, что интеграл этой функции оптимизируется путем подстановки / =tg -^ -. Действительно., ,2Т, Г2,
- 2Т грех х———— — = —— потому что Х 1+t^f’+Z2′ 2dl1-H2′ x=2arctg/, dx Так что это Два./ Один. _ Если вы ставите 7?Я есть(0 = —— , Т?2 (/) = ——- , с правой стороны (8.60) вы получаете Интеграл выражения в форме, которую вы хотите представить (8.58). С DX П Рим ЕР. Вычислить Интеграл 1G — \где>0 » J1+a cos x AU=1. Применение «универсальной тригонометрической замены» 7=tg — ^ — приведет к х-2arc тг т, ДХ — — — -, потому что Х=• — ~а~, &! +Z2 1-H2 (8.60>§3. Класс интегрируемой функции в базовой функции 323 _ dt_____ (a+1) 4-P (1a ) ди Один. 1-1+ Тогда 1) 01 случай следует рассматривать отдельно. Дело 01 Один. 1 / 2 — 1 В , +(/TGT — ‘ 1 / ti Один. / ——— X A2-1 +С. 2°. I n t E g R I R o V A n I d R o b n o-l I n y N s h I R A C I o n a l n O s t e y. в этот момент мы
доказываем интегрируемость в основной функции любой функции вида Где a, B, C и d-несколько констант, а n-произвольное положительное целое число. Такого рода вызовы функций д р о б н о л я н е г О я Р А Ц и о н а л ь н о с т и. Докажем, что интеграл (8>61) функции является ad-Es^O ration-g Ah. Ih символизируется заменой t-l/—. Конечно., Y CX+d ЦТС-Б а-кор’ дуплексный — {ad-be) nt ‘ 1 ‘ 1{a-ctn)2 dt, Так что это {ad-be) ntn~l & {a-ctn) 2 (8.62) 324Ч. 8. Первичные и неопределенные интегралы g-GL AA dtn-b n/L J n/L (ad-be) nt » — 1if put#i (r)= — — — — — — R2 (t)=t, Rs (t) = — ———— — — , a-ctn (a-ctny) далее, в
правой части (8.62), получаем Интеграл выражения вида (8.58), являющийся Интегралом рациональной функции аргумента t.= 1 / —-1—. y e x — / — d П Рим ЕР. Вычислить Интеграл I — 1+x dx „ -1———- . В соответствии с Людмила Фирмаль
1-Х1-х Заменять /=- /A±D=x= -, dx= — ™ — , Есть 1-Х1-х/2 + 1 (12 + 1)2 1 учитывая, что= 2/(/2 +1), получаем 1=2 = 2§d t-2=2t-2 дуга tg / +C= =2l / B; — 2ar’;, g / S+c 3°. И н т е р и П О Н Е В а д р а т н ы х и Р а т и о н н о т е й. В этом отношении R (x, Yax2+BX+C), (8.63) a, b, C являются некоторыми константами. Такая функция называется K V A d R a t i h n o y I R A C I o n A l n O s t u. в этом случае мы, конечно, полагаем, что вторичный тернарный AH2+BX+C не имеет равных корней (в противном случае корни этого тернарного могут быть заменены рациональными). Интеграл функции(8.63) оказывается всегда упорядоченным одним из так называемых П О Д С Т А Н О В О К Е Й л е р а. Сначала рассмотрим
случай, когда вторичное тернарное уравнение AH2+BX+C имеет корень из K o m N l e C n y e. в этом случае знак квадратного трития совпадает со знаком a, а в смысле квадратной тритиевой формулы (извлекается квадратный корень) — n o l O W и te L EN, тогда a>0. Поэтому мы имеем право произвести следующие замены: t=Uax2+BX — + — c + Hua. (8.64)подстановка (8.64) обычно называется П О Д стан О В К О й е й л е р а п ЕР. Мы доказываем, что эта замена рационализирует Интеграл (8.63) функции в случае задачи. Возведение к §3. В базовом классе функций интегральных функций 325 квадратных равенств f ax2B x C-t-X f A обе части, получаем BX+C=? — 2usg1x, верно? И так оно и есть., Под знаком интеграла в правой части (8.65) имеется знак/2-C f A
A t2+S+C от A\o f a / a + bt+C Y a2/A t+b’2V a t+b G(2f a t+b) 2(‘ Итак, в правой части (8.65) мы получаем интеграл от рациональной дроби. Рассмотрим случай, когда квадратный триплет AH2+BX+C имеет корни Xi и x2, не совпадающие с e. В этом случае AH2+BX+C=a (x-xi) (x-x2). В этом случае Интеграл функции (8.63) оказывается упорядоченным подстановкой т. Uax2+BX+C X-XX (8.66) Фактически, если вы квадрат уравнения f A x2+b x4-C=t(x-X±) и уменьшите полученное уравнение на x-XC, вы получите a(x-XG)=■=t2 (x-Xi). ■ dx=^^d t(t2-a) 2 И так оно и есть., Джей Ти?(Х, ф AH2+ьх+с)DX-и Р {- Ах » +Xjt2g(х1-х2—2а(х-Х2) Т Т2-а(Т2-У)2(8.67)326CH. 8. Первичные и неопределенные интегралы дуплексный Правая часть (8.67) под
знаком интеграла представляет собой выражение вида: (8.58) (0=-^F7’2-7″«(0=t2-A g-A-Xy t’). таким образом, в правой части (8.67) Интеграл рациональной дроби выражается в виде: P Lee MA 1) вычислить Интеграл / =\g————-J x-b va4- * 4 * l поскольку квадратный триплет X24-x4-1 имеет комплексные корни, первая подстановка Эйлера/=]LX2 4-x4-1 4-I-уравнение 1/GX2 4-x4-1=T-x квадрат обеих частей. икс= -Я не знаю, что происходит. , (f a=2_2± ‘ ±L iB. 1+21(1+2/) a И так оно и есть., / =2 (f+M J_d z=f f F A+_L_4J/(1 4-2/)3J L i1 4-2/ Д dt (1) 4-2/) 2J Неопределенные коэффициенты A, B,D легко
вычисляются:L=2, B=-3,/)=-3. Наконец/=2 1p / / / —1P|1 + 2 /|+ —- — ‘2 * 2(1 4-2)/) ! =2 1p / / x a+x+1+x / — ^1P|1+2x+2 / x2+x+ 1 | + + —————^ = = — + С. 2(1 4-2x — | — 2ugh2x4-1) дуплексный 2) вычислите Интеграл 1=J2 — ‘ квадратные три члена 1-2x-x2 имеют фактические корни Xj—1 4-и x2—1-1^2, поэтому давайте сделаем следующую замену Эйлера(8.66) Чтобы скрестить обе части уравнения Y1-2x-x? =t (x+1+1^2), мы имеем(-1) (x4-1—) L2)==/2 (X+ 1 + /2 ) ,§ 4. Эллиптический Интеграл 327 Так что это Л — _/2(/2+O+ / 2 — 1 | / 1 _ 2 x_X2 l+Z l-2x — ^=f2+^^ -, d x—— И так оно и есть., I= — 4V2S ———————- J( ^ + 1 ) ^ + 2 / 2 + 1 ) ИТР Получаем интеграл от рациональной дроби, расчет которой предоставляется читателю.
Смотрите также:
| Доказательство иррациональности числа е | Отыскание стационарных точек |
| Вычисление значений тригонометрических функций | Экстремум функции, недифференцируемой в данной точке. |
