Оглавление:
Иррациональные и действительные числа
Покажем, что множество чисел не исчерпывается рациональными числами. В самом деле, возьмём прямоугольный треугольник с катетами, равными 1. По теореме Пифагора, его гипотенуза равна 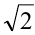 . Докажем, что это число не является рациональным. Приведём старинное доказательство методом «от противного».
. Докажем, что это число не является рациональным. Приведём старинное доказательство методом «от противного».
Предположим, от противного, что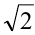 есть рациональное число, тогда его можно представить в виде обыкновенной несократимой дроби
есть рациональное число, тогда его можно представить в виде обыкновенной несократимой дроби 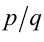 , где
, где 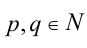 . Тогда
. Тогда  т.е.
т.е.

Левая часть последнего равенства кратна  , следовательно, и
, следовательно, и 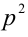 делится на
делится на  . Покажем, что тогда
. Покажем, что тогда 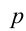 должно делиться на
должно делиться на 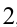 . Действительно, если бы
. Действительно, если бы 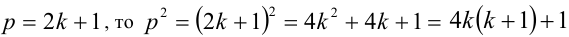 , но тогда
, но тогда  не делилось бы на
не делилось бы на  . Следовательно,
. Следовательно, 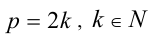 Подставляя в (1) вместо
Подставляя в (1) вместо 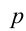 число
число 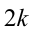 , получим:
, получим: 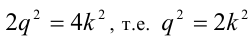 . Отсюда следует, что так как правая часть делится на
. Отсюда следует, что так как правая часть делится на 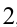 , то и
, то и 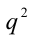 должно делиться на
должно делиться на 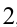 , следовательно,
, следовательно, 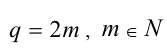 . Но тогда дробь
. Но тогда дробь 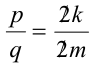 сократима на
сократима на 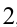 . Полученное противорсчие с несократимостью дроби
. Полученное противорсчие с несократимостью дроби 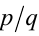 доказывает нерациональность числа
доказывает нерациональность числа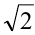 .
.
Таким образом, существуют числа, не являющиеся рациональными, которые нельзя представить в виде отношения двух целых чисел. Расширим множество чисел, вводя понятие иррационального числа.
Иррациональным называется число, представимое в виде бесконечной десятичной непериодической дроби. Название «иррациональный» происходит от латинского ‘irrational’ — безрассудный, не определяемый отношением. Специального обозначения для множества иррациональных чисел (их, как и рациональных чисел, бесконечно много) не существует.
Открытие иррациональных чисел приписывают пифагорейцам (V век до нашей эры), которые доказали, что гипотенуза равнобедренного прямоугольного треугольника несоизмерима с его катетом, т.е. установили иррациональность числа 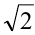 . Однако это открытие противоречило всей пифагорейской философии, в основу которой были положены только натуральные и рациональные числа. Поэтому оно сохранялось в строжайшей тайне. Существует легенда, повествующая о том, что пифагореец
. Однако это открытие противоречило всей пифагорейской философии, в основу которой были положены только натуральные и рациональные числа. Поэтому оно сохранялось в строжайшей тайне. Существует легенда, повествующая о том, что пифагореец
Гиппас, раскрывший людям секрет иррациональности  , погиб в море по воле разгневанных богов.
, погиб в море по воле разгневанных богов.
Примеры иррациональных чисел: 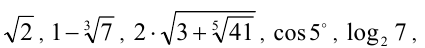


Для решения экзаменационных задач обычно достаточно знать, что
Львовский 33-летний профессор-нейрохирург Андрей Тихонович Слюсарчук публично продемонстрировал, что помнит миллион цифр после запятой у числа 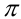 . Это новый мировой рекорд (предыдущее достижение было зафиксировано у 59-летнего японца Тиби Акири Харагучи, который запомнил 83431 знак числа
. Это новый мировой рекорд (предыдущее достижение было зафиксировано у 59-летнего японца Тиби Акири Харагучи, который запомнил 83431 знак числа 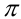 ). Рекорд поддался со второй попытки. Говорят, миллион цифр из книги на 250 страниц Андрей запоминал 6 дней. Достижение занесено в книгу рекордов Украины и уже заявлено для регистрации в Книгу рекордов Гиннеса. Новая задача для Слюсарчука — запомнить уже не один, а 5 миллионов цифр числа
). Рекорд поддался со второй попытки. Говорят, миллион цифр из книги на 250 страниц Андрей запоминал 6 дней. Достижение занесено в книгу рекордов Украины и уже заявлено для регистрации в Книгу рекордов Гиннеса. Новая задача для Слюсарчука — запомнить уже не один, а 5 миллионов цифр числа 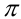 (газета «Московский комсомолец» от 27 марта 2006 года).
(газета «Московский комсомолец» от 27 марта 2006 года).
Если объединить непересекающиеся множества рациональных и иррациональных чисел, то полученное бесконечное множество называется множеством действительных (вещественных) чисел и обозначается буквой R (по-английски ‘real’ — действительный, реальный). То есть действительные числа -это числа, представимые бесконечными десятичными дробями. Строгая теория действительных чисел была построена математиками лишь в XIX веке (Больцано, Вейерштрасс, Кантор, Дедекинд и др.). Из определения множества действительных чисел следует, что 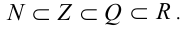
Пример №85.
Доказать, что число 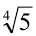 не является рациональным числом.
не является рациональным числом.
Доказательство (методом от противного). Предположим, что 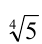 есть рациональное число, тогда оно представимо в виде
есть рациональное число, тогда оно представимо в виде 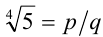 , где
, где 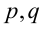 — взаимно простые натуральные числа. Перепишем равенство в виде
— взаимно простые натуральные числа. Перепишем равенство в виде 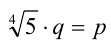 и возведем его в 4-ю степень:
и возведем его в 4-ю степень: 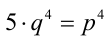 . Так как левая часть кратна 5, то и
. Так как левая часть кратна 5, то и 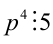 , а значит, р кратно 5, т.е.
, а значит, р кратно 5, т.е. 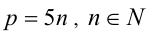 . Подставив в равенство
. Подставив в равенство 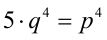 вместо р выражение
вместо р выражение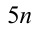 и сократив на 5, получим новое равенство
и сократив на 5, получим новое равенство 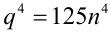 , откуда следует, что
, откуда следует, что 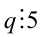 . В результате оба числа р и q оказались кратны 5, что противоречит их взаимной простоте. Следовательно, предположение о рациональности числа
. В результате оба числа р и q оказались кратны 5, что противоречит их взаимной простоте. Следовательно, предположение о рациональности числа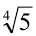 было сделано неверно, что доказывает иррациональность этого числа.
было сделано неверно, что доказывает иррациональность этого числа.
Пример №86.
Доказать иррациональность числа 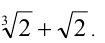
Решение:
Воспользуемся методом от противного. Предположим, что это рациональное число, тогда его можно представить в виде обыкновенной дроби:
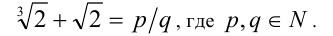
Перепишем равенство в виде 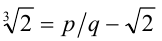 и возведём его в куб:
и возведём его в куб:
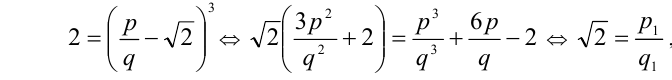
где 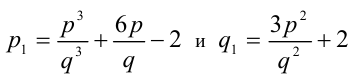 — рациональные числа и поэтому их отношение
— рациональные числа и поэтому их отношение 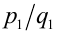 также рационально. Получили противоречие, так как
также рационально. Получили противоречие, так как 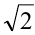 -иррациональное число (доказано выше). Значит, предположение о рациональности числа
-иррациональное число (доказано выше). Значит, предположение о рациональности числа 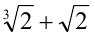 было неверно и данное число иррационально, что и требовалось доказать.
было неверно и данное число иррационально, что и требовалось доказать.
Пример №87.
Доказать иррациональность числа 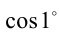 .
.
Решение:
Воспользуемся также методом от противного. Предположим, что это рациональное число. Складывая два очевидных тождества
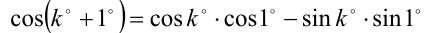
и
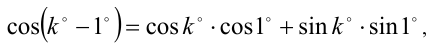
получим вспомогательное тождество
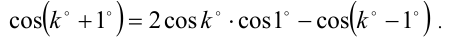
Подставим в это тождество вместо к последовательно числа 1, 2, 3,…,
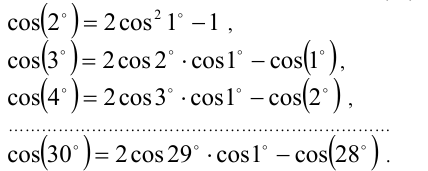
Видим, что если 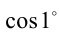 рационален, то рациональным будет и
рационален, то рациональным будет и 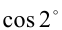 , а тогда и
, а тогда и 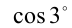 и т.д. Таким образом, придём к тому, что
и т.д. Таким образом, придём к тому, что 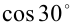 также будет рационален, поскольку выражается через рациональные числа посредством арифметических операций умножения и вычитания, не выводящих, как известно, за пределы множества рациональных чисел. Пришли к противоречию с тем фактом, что, с другой стороны,
также будет рационален, поскольку выражается через рациональные числа посредством арифметических операций умножения и вычитания, не выводящих, как известно, за пределы множества рациональных чисел. Пришли к противоречию с тем фактом, что, с другой стороны, 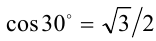 — иррациональное число. Это противоречие и доказывает утверждение об иррациональности
— иррациональное число. Это противоречие и доказывает утверждение об иррациональности 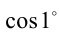
Пример №88.
Доказать иррациональность числа 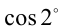
Решение:
Предположим от противного, что 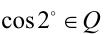 , но тогда, используя формулы
, но тогда, используя формулы 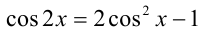 и
и 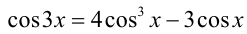 , получим, что числа
, получим, что числа 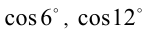 ,
, 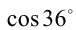 также будут рациональны. Покажем, что в действительно-сти число
также будут рациональны. Покажем, что в действительно-сти число 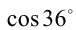 иррационально (полученное противоречие будет доказывать иррациональность
иррационально (полученное противоречие будет доказывать иррациональность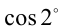 ). Вычислим его значение. Известно, что
). Вычислим его значение. Известно, что 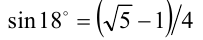 (если вам не знаком этот факт, то предварительно докажите его), тогда
(если вам не знаком этот факт, то предварительно докажите его), тогда 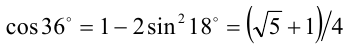 — иррационально.
— иррационально.
Пример №89.
Доказать иррациональность числа 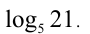
Решение:
Предположим, от противного, что данное число рационально. Тогда, по определению рационального числа, его можно представить в виде несократимой обыкновенной дроби 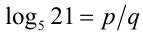 , где
, где 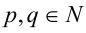 . Последовательно преобразовывая равенство с помощью свойств логарифмов, приведём его к виду
. Последовательно преобразовывая равенство с помощью свойств логарифмов, приведём его к виду
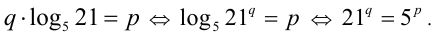
В последнем равенстве левая часть кратна 3, а правая — нет, что невозможно. Полученное противоречие говорит о том, что сделанное ранее предположение о рациональности данного числа было неверным, а значит, число иррационально.
Пример №90.
Существуют ли рациональные числа x,y,u,v, удовлетворяющие уравнению
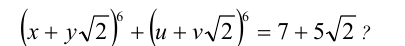
Решение:
Убедимся в справедливости следующих двух утверждений.
1.Если a,b,c,d -рациональный и 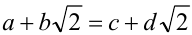 , то
, то 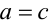 и
и 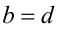 .
.
Действительно, так как 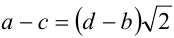 , то или
, то или 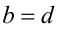 , следовательно,
, следовательно, 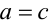 , или
, или 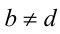 , тогда
, тогда 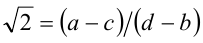 , что невозможно, потому что
, что невозможно, потому что 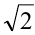 — иррациональное число, а
— иррациональное число, а 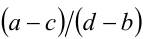 — число рациональное.
— число рациональное.
2.Если а,b — рациональные числа, то 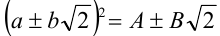 , где числа А, В — рациональные.
, где числа А, В — рациональные.
Справедливость данного утверждения следует из следующей выкладки:
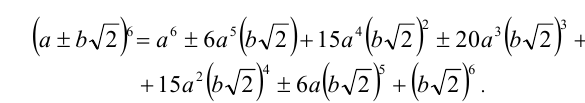
Пусть теперь x,y,u,v — рациональные числа, и выполняется равенство
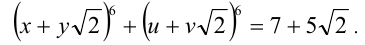
Тогда согласно утверждениям 1 и 2 имеем
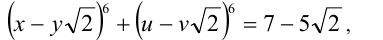
однако последнее равенство невозможно, поскольку его левая часть неотрицательна, а число 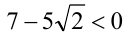
Ответ: такие числа не существуют.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
