Оглавление:
















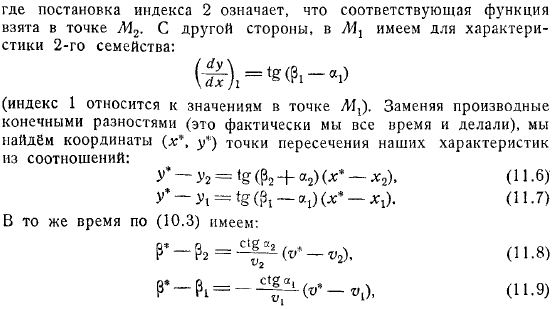

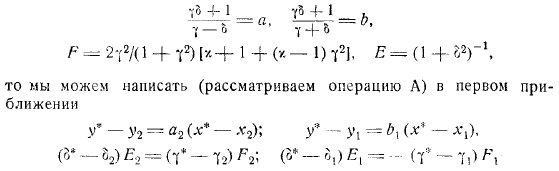


Использование характеристик для решения плоской безвихревой задачи
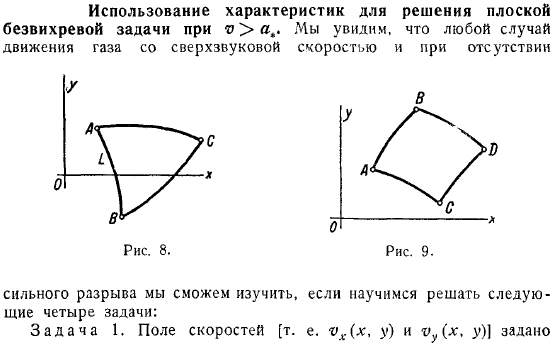
Газ движется со сверхзвуковой скоростью. Если вы научитесь решать следующие задачи, то сможете заглянуть в сильный пробел. Вызов. Набор полей скорости. В плоскости по дуге проходят некоторые линии, которых нет.
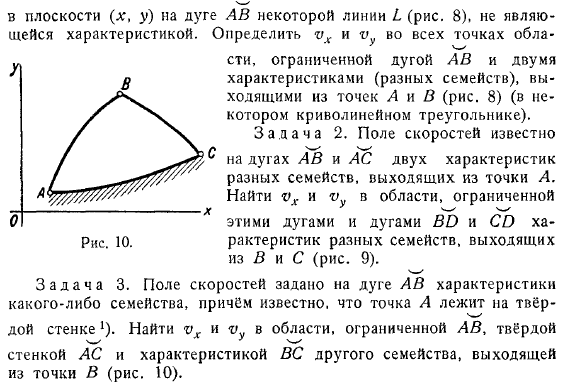
Определяется всеми точками области, окруженной дугами, и характеристики (различные семейства) появляются из точек (некоторые изогнутые треугольники). Известное поле скоростей характерных дугах разных семейств решения задач по гидромеханике, которые выходят из точки. Поиск в ограниченном пространстве.
- Эти дуги и дуги различных семейных характеристик возникают. Иизвестно, что поле скорости задается на дуге характеристики семейства, а точка находится на сплошной стенке.
- Поиск в ограниченной твердой области. Еще одна семейная стена и особенности, выходящие из точки вызов.
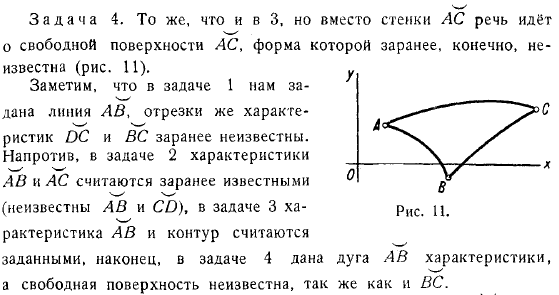
И то же самое, но вместо стены, мы будем говорить о свободной поверхности. Людмила Фирмаль
Конечно, его форма заранее неизвестна. Обратите внимание, что линия дана в выпуске, но сегмент характеристики не известен в. Дело, напротив, в том, что характеристика считается заранее известной (неизвестной), а в задаче рассматриваются характеристика и схема.
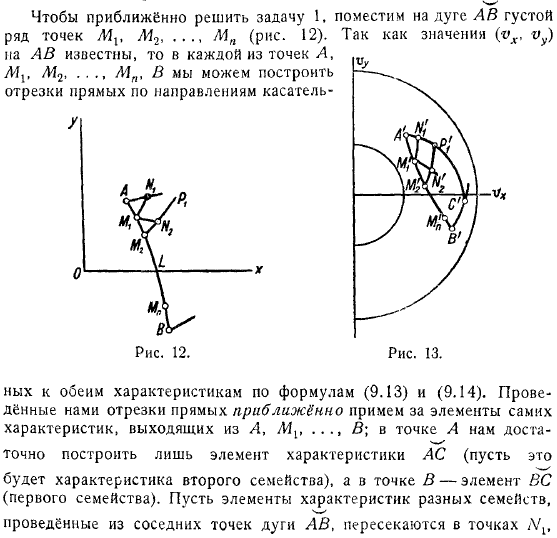
Наконец, задача задается характеристической дугой, и свободная поверхность также неизвестна. Чтобы решить проблему почти. Нарисуйте толстую дугу. Многие точки. Значение известно, поэтому в каждой точке.
- Вы можете построить отрезок линии в направлении касательной с помощью. По формуле к обеим характеристикам. Отрезки нарисованных нами линий почти считаются элементами самих характеристик, которые приходят.
- В какой-то момент достаточно построить только элементы характеристики (разрешить это).
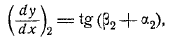
Есть семейная характеристика, а в то время-это элемент (первой семьи). Давайте рассмотрим элементы характеристики различных семейств. Пересекаются в точке, проведенной из соседней точки дуги (Например, есть пересечение элементов характеристики семейства и элементов характеристики первого семейства).
Чтобы найти в точке, выведите вот так. Людмила Фирмаль
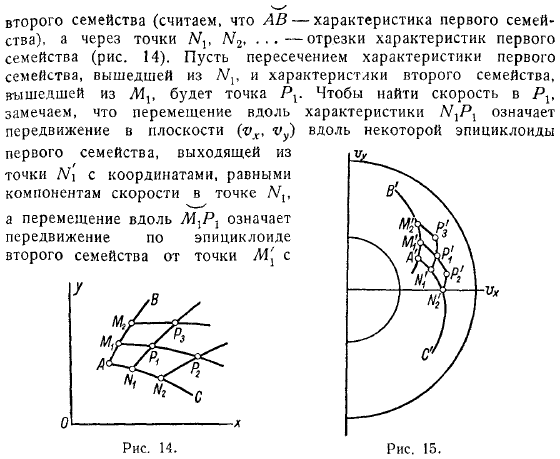
Обратите внимание на скорость точек в плоскости. Пусть это будет точка. Если вы двигаетесь в плоскости по характеристикам семейства от точки, то вы будете двигаться вдоль плоскости по ЭПИ-циклоиде семейства и от плоскости по ЭПИ-циклоиде первого семейства.
Вы можете предварительно нарисовать оба ЭПИ-циклона, которые вам нужны, чтобы вы могли найти их пересечение хотя бы графически понятно, что координаты точки дают скорость точки. Аналогично найдите скорость точек. Ниже мы укажем очень удобную технику для графического определения скорости в этих точках.
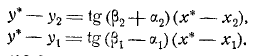
Теперь вы можете использовать много точек в качестве стартовой сети и выводить их таким же образом, как вы описали это известная скорость. Таким образом, во всех этих точках характеристики обоих семейств могут быть построены по уравнению или как нормаль плоской эпициклоиды перед пересечением в точке, но скорость этих точек можно найти как координаты пересечения эпициклоны, проходящих через точки вы постепенно заполняете всю кривую Проблемный треугольник в вопросе.
Изначально неизвестная линия создается сама собой(примерно, как в пунктирной линии, она применяется не к гладкой кривой, а ко всем характеристикам). Поэтому плотная плоская безвихревая сетка точек (эта плотность Зависит от плотности точек нашего «треугольника») мы будем знать скорость. Если вспомнить, что скорость направлена вдоль биссектрисы угла между характеристиками, то можно легко определить текущую линию.
Давление основано на уравнении Бернулли. Проблема была решена. Решение задачи принципиально не отличается от решения задачи. Поместите толстый ряд точек на характеристику, а толстый ряд точек на характеристику все эти очки вам дадут скорость.
- Далее прорисовываем элементы характеристики через точки семейство (считается первой семейной характеристикой), сегмент первой семейной характеристики через точки. Точкой будет пересечение признаков первого и второго. To найти скорость, движущуюся вдоль характеристического средства, движущегося вдоль ЭПИ-циклоиды семейства из точки с, оставляя точку с координатами, равными компоненте скорости точки, движущейся в плоскости вдоль ЭПИ-циклоиды первого семейства.
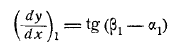
- Координата-составляющая скорости в точке. Пересечение ЭПИ-циклоид выше дает компонент скорости. Зная скорость движения в определенной точке, можно провести оба объекта через эту точку, до точки пересечения с элементами объектов кланов, соответственно, до точки отправления.
To найдите скорость, выведите ее точно так же, как при рассмотрении точек. Только роль предыдущей точки играет точка, роль точки играет, и точка должна быть поставлена. То же самое можно сказать и о точках. Если вы продолжите составлять дальше, в сетке характеристик, постепенно охватите весь изогнутый четырехугольник, описанный в пересечение последних можно узнать где угодно.
Обтекаемая линия
Обтекаемая линия работает как биссектриса между касательными характеристики, а давление выводится из уравнения Бернулли. Задача будет решена. Все указанные точки находятся на одном и том же эпизикоиде семейства, и те же точки.
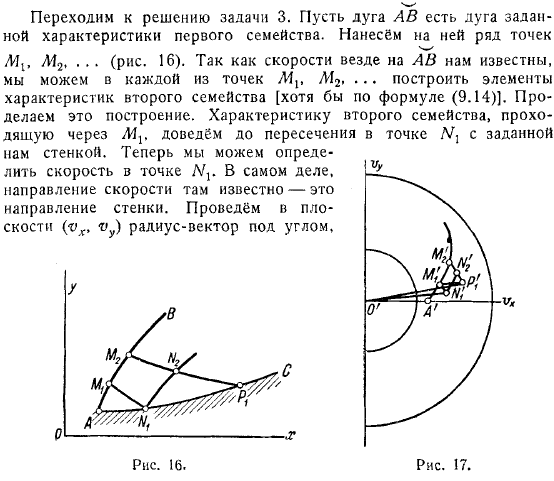
Первая семья и лежала в том же ЭПИ-Киличе. Оба этих ЭПИ-циклона выходят наружу. Приступайте к решению поставленной задачи. Пусть дуга — это дуга определенной характеристики первого семейства. Нарисуйте на нем несколько точек.
Зная скорость в любом месте, в каждой точке можно построить элементы характеристик семейства. Мы будем заниматься этим строительством. Приведем к пересечению с заданной стенкой характеристики проходящего семейства.
Теперь вы можете определить скорость на определенном дело в том, что направление скорости, которая там есть, известно — это направление стены. Нарисуйте радиус-вектор выхода из отверстия, повернув плоскость под углом. Равен углу между направлением касательной к траектории и осью.
Где-то в этом радиус-векторе нам нужно искать точку, координаты которой дают скорость в этой точке. С другой стороны, дело в характеристиках семейства, которые вытекают из точки. Сопоставляет точку с точкой на плоскости.
Проходя через ЭПИ-циклоиду семейства и достигая пересечения с упомянутым выше радиус-вектором, мы встречаемся с последним в точке, где координаты скорости выявляются в точке. Знание скоростных и строительных характеристик на самолете. От первого семейства до скрещивания появляются черты семейства.
Скорость определяется как координаты точки пересечения первой ЭПИ-циклоиды. Семья проходит, и семейство эпизиоклоидов проходит. При черчении из обоих объектов первый элемент семейства переносится на пересечение с символом. Из характеристик семейства и по характеристикам семейства нарисуйте (точка) перед пересечением контура.
Входной сигнал скорости подобен скорости. To найти скорость, заметить, что направление скорости известно (так, чтобы направление скорости было известно) и построить радиус-вектор в этом направлении в плоскости. Скорость знайте скорость и выполните характеристику там.
Наша проблема будет решена. Обратим внимание на очень важный частный случай проблемы. Предположим, вы знаете, что вдоль скоростной характеристики всюду одно и то же постоянное значение и направление.
Этот случай имеет место, например, в задаче обтекания крыла неограниченным потоком с постоянной величиной и скоростью дело в том, что если запустить этот профиль из определенной точки, то неограниченный поток будет выполняться слева со скоростью, параллельной оси. Затем по характеристике производится переход от прямого подхода к контуру чтобы обтекать петлю.
Вместе с характеристиками,»прилипание» различных движений происходит как характеристика. Это может быть такая слабая прерывистая линия), величина и направление которой постоянны на всем протяжении скорости, равной скорости набегающего потока. Обратите внимание, что в этом случае строка будет дело в том, что градиент вдоль этой кривой, выраженный с помощью формулы, везде одинаков.
Потому что правая часть состоит только из компонентов. Скорость, и они считаются вместе постоянными. Так что давайте соберем его везде.Обратите внимание на характеристики второго семейства и т. д.
Вдоль них, согласно формуле. Где находятся различные константы, характеризующие индивидуальные особенности семьи. Последний признак пересекается в определенных точках. Именно такой образ. Поэтому надо. Форма уравнения для соединения вдоль выглядит следующим образом.
Однако, когда точно такое же соотношение удовлетворяется. Потому что именно на ней и должна быть эта линия. В нашем случае скорость и угол во всех точках между контуром и характеристикой связаны отношением к одной и той же константе, но в общем случае константа изменяется для каждой характеристики.
Отношение здесь играет роль дополнительного конечного отношения, связывающего компонент скорости (который можно назвать). Используя это соотношение, можно решить задачу и решить только уравнение в частных производных уровня с целевой функцией (напомним, что в общем случае существует системы уравнений с функциями), то есть в конечном счете нормальный дифференциал.
To получим это уникальное уравнение, опишем условие, при котором отсутствуют вихри, например, выраженное через можно далее различать и описывать, помня, что это было связано отношениями. Или (потому что мы имеем дело со свойствами семейства), где угол Маха, после выполнения простого преобразования, мы можем написать.
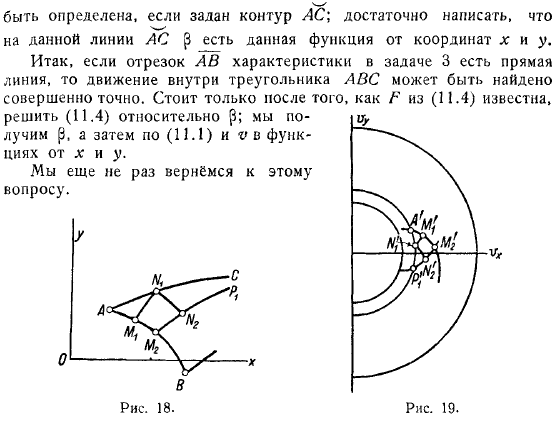
Это дифференциальное уравнение в частных производных задается интегрированием следующего. Определяет, задан ли контур. Напишите, что в этой строке есть определенная функция координат. Так, если сегмент рассматриваемой характеристики является прямой линией, то можно точно найти движение в треугольнике.
Это первый раз, когда я знаю, что должен принять решение. Получить его, а затем получить его по функции. Мы будем возвращаться к этому вопросу снова и снова. Давайте перейдем к решению проблемы.
Дадим скорость вдоль некоторой характеристической кривой (например, семейства) и познакомимся с тем, что находится на свободной границе необходимо выяснить форму свободной поверхности и движение между характеристиками первого семейства, чтобы пройти.
Приложите много очков. Рисует элемент линии, направленной вдоль известной скорости в точке через точку. Рассмотрим этот элемент как элемент свободной поверхности, через которую он проходит. Затем нарисуйте характеристики первого семейства в точке пересечения с этим элементом на свободной поверхности (это и есть определение свободной поверхности).
Это означает, что скорости всех точек на свободной поверхности будут везде одинаковыми согласно уравнению Бернулли. Поэтому давайте построим круг радиуса в. To определив направление скорости точки, достаточно найти точку пересечения эпизиотиков первого семейства в плоскости, поскольку она находится на свободной поверхности.
Координаты точек первой семье известны компоненты скорости точек окружности. Для определения скорость в определенной точке, то, как отрезок прямой, направленной вдоль этой скорости, строит непрерывную свободную поверхность. Нарисуйте элементы характеристик семейства до пересечения с элементами характеристик первого семейства.
Скорость определяется как пересечение эпициклоида первого семейства и эпициклоида второго семейства. Зная скорость, выполняйте характеристики первого семейства до тех пор, пока они не пересекутся с элементами свободной поверхности в определенной точке. Проблема будет решена.
Прежде чем приступить к применению газовой динамики к конкретным задачам, скажем несколько слов об оценке погрешности описанного здесь метода. Нетрудно заметить, что решение всех задач основано на возможности использования следующих операций.
Операция. Скорость задается соседними точками на плоскости. Найти скорость на пересечении характеристик различных семейств, которые выходят из. To для выполнения этой операции достаточно найти точку пересечения эпизиоидов разных семейств, где координаты появляются из точки на плоскости, являющейся определенной составляющей скорости точки.
Операция. Скорость в определенной точке на плоскости известна. Дана лайн. Это не характеристика (точка находится рядом с ней), по которой можно увидеть направление (или величину) скорости. Найти величину (или направление) скорости в данной точке. Удовлетворяет символу, который исходит из строки.
Здесь мы находим точку на плоскости с координатами, равными заданному значению в этой точке, и рисуем эпиксит до тех пор, пока он не пересечет радиус-вектор, параллельный направлению скорости в (или до тех пор, пока он не пересечет окружность, соответствующую известному значению скорости). Например, рассмотрим операцию подробнее. To будьте точны, только половина этой операции может быть выполнена.
Вы можете найти точки, то есть скорость точки. Однако расположение последней точки неизвестно, так как тип характеристики в плоскости заранее не известен. Однако можно создать сегмент точек, которые касаются характеристик.
Эти сегменты примерно принимают за характеристики. Пересечения этих отрезков скорее дают точки, но если есть четкая связь, то каждая кривая дуги характеристики может быть заключена под определенным углом, и вместо этого оценивается погрешность, возникающая из факта. To сделайте это, используя ранее упомянутые.
Его очевидная зависимость только доказывает, что это делается без особого труда, что наклон касательной к характеристике изменяется монотонно вдоль соответствующего участка характеристики (см. уравнение эпитета). Если это так, то проведите его через отрезок, параллельный направлению касательной. Это направление можно вычислить заранее, но положение точки в плоскости неизвестно и определяется с его помощью точно.
Касательная к другой характеристике, можно констатировать. Все характерные изогнутые дуги находятся внутри угла. Дуга находится внутри угла. Поэтому точность расчетов зависит только от степени близости точек.
- Все поставленные здесь задачи решаются путем построения на плоскости характеристик обоих семейств, скорость которых проходит через известные в то же время я всегда ссылался на формулу, которая всегда могла вычислить направление.
- Этот расчет элементарен, но есть еще необходимость в таком неприятном расчете, как извлечение корня предоставил графический метод для быстрого определения направления характеристики в плоскости (точка, скорость которой известна). Скорость точки на плоскости.
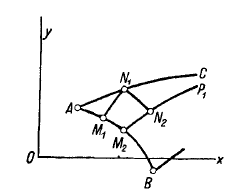
- Отметьте точки на плоскости с соответствующими координатами, центрированными в начальной точке, и нарисуйте эллипс с равной половиной в общем, нетрудно заметить, что таких овалов.
- Вы можете видеть, что большие оси этих эллипсов просто параллельны свойствам, проходящим через плоскость через. To докажите это, представив, что вектор скорости точки разложен на составляющие.
Вдоль касательной характеристики
Вдоль касательной характеристики, проходящей через плоскость (например, первое семейство), вдоль нормалей этой характеристики На самолете. Мы это знаем. Обратимся к уравнению Бернулли и заменим его. Затем, когда вы собираете и делите термины, вы получаете отношения.
Теперь проецируем радиус-вектор на большую ось нарисованного эллипса и радиус, перпендикулярный ей. Первая проекция — это проекция. А затем построив эллипс. С другой стороны, для точки величина может удовлетворять линейным уравнениям, равным величине, и поэтому.
- В результате направление большой оси эллипса совпадает с направлением проходящей характеристики, а направление малой оси совпадает с направлением нормалей этой характеристики.
- Метод построения характеристики в плоскости, описанный здесь, подходит не только для без спирали, но и для случая вихрей, естественно. Это связано с тем, что он одинаково действителен для обоих этих случаев.
Здесь рассматриваемый овал (назовем его боуджмановским эллипсом) можно приготовить сразу на прозрачной бумаге (или целлулоиде). Объедините этот центр с началом координат и вращайте его вокруг начала координат до тех пор, пока точка, заданная в плоскости скорости точки, не станет эллипсом. Все, что остается, это сломать направление длинной оси эллипса в этом положении в плоскости.
Найдите направление прохождения характеристик. Направление характеристики определяется как направление главной оси возможного положения эллипса. Эллипс Бусемана также позволяет строить характеристики в плоскости, т. е. дело в том, что оказывается, что характеристики плоскости (эпитеиды) ортогональны (другому числу) характеристик плоскости.
Направление длинной оси эллипса Буземана совпадает с направлением характеристики в плоскости. То есть направление малой оси (перпендикулярно большой оси) совпадает с направлением эпизиоида (другого семейства). Поэтому, чтобы построить элементы ЭПИ-циклоиды, которые проходят через нас, достаточно пройти через овал Бусемана и построить параллельный основной сегмент от малой оси овала.
При постройке имеется ЭПИ-циклон Теперь, когда вы устанавливаете индекс, вы получаете соответствующую функцию в точке. С другой стороны, мы должны охарактеризовать семью. Индекс относится к значению точки.
- Заменить производную на конечную разность (мы делали это практически все время) и найти координаты точки пересечения характеристики из соотношения. Здесь значения этих функций находятся в определенный момент времени. Поэтому они определяются из системы линейных уравнений.
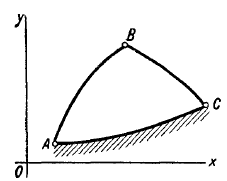
Также к коэффициентам этой системы относятся тригонометрические функции. Элерс предложил адаптировать расчет с использованием характеристик электронной вычислительной машины следующим образом. Новые величины, поскольку искомое количество не должно приниматься).
Для этих новых значений соотношение характеристик принимает следующий вид. В то же время. Итак, после основных расчетов Поэтому она написана в следующем виде. Коэффициент является алгебраической функцией.
Сам расчет должен выполняться итерацией. То есть, если мы введем следующую нотацию, чтобы уменьшить символ. Тогда можно писать в первом приближении(с учетом операции). Или, вы можете использовать эти уравнения.
Таким образом, новый приближение. Этот процесс должен повторяться до тех пор, пока не будет достигнута требуемая точность. На протяжении всего этого раздела мы несколько раз говорили об ограничениях, в которых наши рассуждения были например, в интересующей области не было сильных разрывов и предполагалось отображение плоскости(что было важно при оценке погрешности приближенных метров).
Здесь мы описываем движение, которое происходит с дозвуковой скоростью в одних частях плоскости и со сверхзвуковой скоростью в других. Вслед за Христиановичем мы возвращаемся к детальному и скрупулезному рассмотрению всех случаев, которые могут иметь место на сверхзвуковых станциях. Далее мы рассмотрим отдельные простые примеры конкретно.
