Кеплерова задача

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

Кеплерова задача

Проблема Кеплера Наиболее важным случаем центрального поля является следующее поле Его потенциальная энергия обратно пропорциональна r, Следовательно, сила обратно пропорциональна r2. К ним относятся ньютоновское гравитационное поле и кулоновское электростатическое поле.

Первый, как известно, имеет природу притяжения, а второй может быть как областью притяжения, так и отталкивания. Сначала рассмотрим области притяжения. U = -os / г (15,1) Используйте положительную постоянную ОС. «Эффективный» график потенциальной энергии + & <15’2> Он имеет форму, показанную на рисунке. 10.

стремятся к нулю на отрицательной стороне Существует минимальное значение Людмила Фирмаль

Когда r- »0, она поворачивается c + os и r-uc r = M2 / ost равных (^ Ef) ww = (15,3) Из этого графика, когда E> 0, движение частицы бесконечно, а E <0- Компактно поддерживается. Форма траектории получается по общей формуле (14.7).

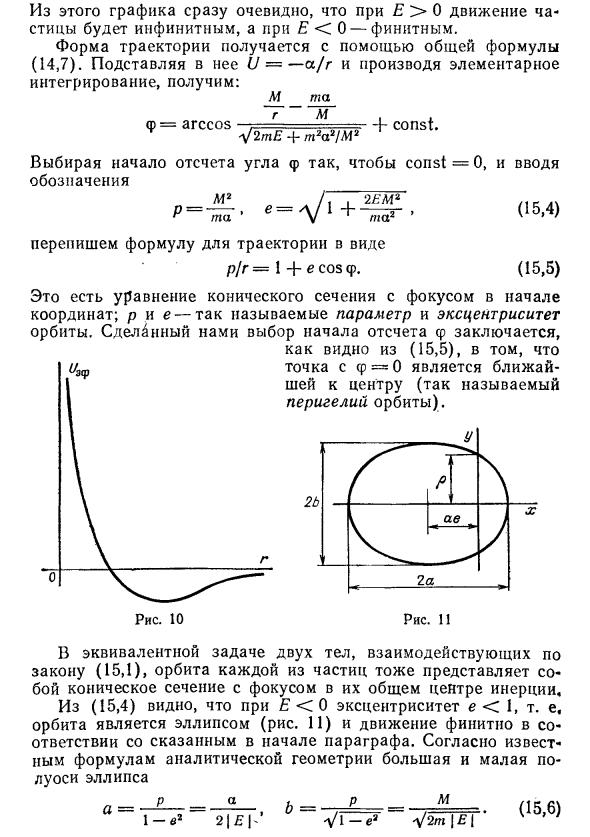
Генерируется путем замены U = -os / г Основную интеграцию получаем М / г-тосс / М, w = arccos. » + const ^ 2tE + t2oc2 / M2 Выберите начало угла φ так, чтобы const = 0, и введите обозначения M2 L. 2EM2 p = -, e = \ 1- \ ——-, (15-4) ToS U Ta2 VY Перепишите орбитальную формулу в p / r = 1 + эко ф. (15,5) Это коническое уравнение, ориентированное на происхождение. р и е так называемые параметры и эксцентриситет Orbit.

Выбор контрольной точки f Как видно из (15.5), точка с φ = 0 является ближайшей Вокруг шеи (так называемый перигелий орбиты). Эквивалентная задача двух взаимодействующих объектов Для конуса (15.1) траектория каждой частицы также представляет собой коническое сечение, ориентированное на общий центр инерции.

(15.4) показывает, что при E <0 эксцентриситет равен e <1. Орбита представляет собой эллипс (рисунок 11), и движение является конечным в соответствии с тем, что было указано в начале раздела. Согласно известной формуле аналитической геометрии, большая и малая полуоси эллипса (хтрМ (л- а = — * = Ь´Ь = Ж ^ = 7ЩЩ- (5 ‘в) Минимально допустимое значение энергии соответствует (15.3).

Большая полуось эллипса зависит только от энергии частицы Людмила Фирмаль

В этом случае e = 0, то есть эллипс рисуется в виде круга. ОБРАТИТЕ ВНИМАНИЕ (но не от момента). Минимальное и максимальное расстояние до центра поля (эллиптическая фокусировка) равных ^ • -p-a (1-е), е + 1 (15,7) ^ max-11-e-ft (l + c).

Эти формулы (а и е в (15.6) И (15.4)) Конечно, вы можете получить непосредственно в качестве корня уравнения? 7eff (r) = E. Для времени эллиптической орбиты, т. Е. Периода движения T, удобно определить, используя закон сохранения моментов в форме «интегрирования площади» (14.3).

Интегрирование этого уравнения по времени от нуля до T дает: 2t f = TM, / Это орбитальная область. Для эллипса / = = наб, и используя формулу (15.6) T = m— = pos OS 2 | Y1: (15.8) Рисунок 12 Площадь периода Пропорционально кубу с линейными размерами Орбита уже показана в §10.

Также отметим, что этот период зависит только от энергии частиц. Если E ^ 0, движение бесконечно. Если E> 0, эксцентриситет e> 1, то есть локус является гиперболической оболочкой Как показано, центр поля (фокус). 12. Расстояние перигелия от центра где = р = е + 1 а (е-1) ~ e2-1 «2E Гипераксис «полуоси». Когда Е = 0, эксцентриситет равен е = 1, то есть движение частицы Бегите по параболе с расстоянием перигелия rmin = p / 2.

Это Случай реализуется, когда частицы начинают двигаться От бесконечного отдыха. Зависимость координат частицы от времени при движении На орбите это можно найти с помощью общей формулы (14.6). Отображение в удобном параметрическом формате Следующим образом.

Сначала рассмотрим эллиптическую орбиту. Введите a и e согласно (15.4) и (15.6) и опишите интеграл (14.6), который определяет время, в следующем формате: ^ _ Я т д д г _ / та я г д 2 \ E \ J I a M2 Va J \ D2e2 ~ (r ~ a) 2 ~ R2 + ni r ~ 2m \ E \ Использование естественного замещения r-a = —ae cosЈ, Этот интеграл t = y r ^ ~ J (1-e cos l) d l = s j r ^ ~ (Ј, -еsinЈ,) + const.

Выберите ссылку на время для преобразования в постоянную Если ноль, наконец получить следующий параметр параметра зависимости t от r. r = a (1-ecosЈ,), t = esinЈ,) (15.10) (В момент t = 0 частицы находятся в перигелии). Через то же самое Параметр Ј,

Декартовы координаты частиц также могут быть выражены x-g cos f, y = g sin f (ось x и ось y Эллипс большой и малой полуосей). Из (15.5) и (15.10) ex = p-r = a (1-e2) -a (1-ecosЈ,) = ae (cos-e), И мы найдем, как \ / r2-x2. В конце: x = a (cosЈ, -e) ,? / = ay / 1-e2 sin (15.11) Полное вращение эллипса учитывает изменения параметров paЈ, от нуля до 2тг.

Очень похожий расчет гиперболы Орбита приводит к результатам r = a (e c h Ј, -1), t = l / w a 3 / (X (e s h Ј, -Ј,), V ‘V _ ‘ (12/15) x = a (e-chЈ,), y = a \ / e2-1 shЈ ,, Параметр значение между –os и + oc выполняется. Вернитесь к движению отскок поля. и = «(15.13) (Os> 0). В этом случае эффективная потенциальная энергия Tt- “-L m2 E (^ g 2 mr2 При изменении r от нуля до осей оно монотонно уменьшается от + ос до нуля.

Энергия частицы может быть только положительной, а движение всегда бесконечным. Все расчеты в этом случае точно такие же, как и расчеты, выполненные выше. Траектория преувеличена = -1 + e cos cf (15.14) (P и e определяются предыдущим уравнением (15.4)). Она проходит через центр поля, как показано на рисунке. 13.

Перигелий расстояние rmin = a (e + 1). (15.15) Рисунок 13 Зависимость от времени задается параметрическим уравнением r = a (echЈ, + 1), t = A / ^ (eshЈ, + Ј), (15.16) x = a (chЈ, + e), y = ay / e2-1 sh В конце раздела указано, что существует интеграл движения при перемещении поля U = os / g (произвольный знак ОС). Специфично для этой области.

Простая проверка прямым расчетом [vM] + ^ = const. (15.17) На самом деле, его общая производная по времени [м] + ^ Или заменить на M = m [rv]. / • \ /. ч, ав ар (вр) rar （^ vv） -mv ^ rv ‘+ f — p- / p% j Где установлено согласно уравнению движения mv = a r / r3, Вы можете видеть, что это выражение исчезает. Сохраненный вектор (15.17) направлен вдоль главной оси Это тот же размер, что и ось от фокуса до перигелия.

Это легко Если вы считаете значения перигелия, вы можете увидеть все. Интеграл движения (15.17) и интегралы M и E являются уникальными функциями состояния ( Жизнь и скорость) частицы. В § 50 мы видим, что появление таких дополнительных уникальных интегралов связано с так называемым двигательным вырождением.

Задание 1. Найти временную зависимость координат частицы при движении в поле U = -os / g с энергией E = 0 (парабола). Решения. С интегральной Младший доктор т = 2а М -г ~ — 2 т? Для того, чтобы заменить М; (! + L 2) =? (1 + L2) 2tos 2 В результате мы получаем следующий параметр представления желаемой зависимости. x = | (1-l 2), y = t- Параметр r \ выполняет значение от -su до + oo. 2.

Интегрировать уравнение движения цены в цену (X ral field u = ——, a> 0. Грамм 2 Решения. Используя формулы (14.6) и (14.7), выберите соответствующий источник (положите, E * Pn) π, ηM2 1 I (2 2m > 0, -> a- = ^] ^ _ ^ _ cos ^ 1-_ ч M 1/2 т E (2т б) если E> 0, — <a- = \ ———— sh (p \ ———- 1 в) Если E <0, — <a- = \ ———! ch f4 / ———- 1 7 2т г В 2ша-М 2 Г В М 2 Все три случая 1 т t = — \ — \ Er2 ——- h os. E y 2 V 2 t В случае б) и в) частицы «падают» к центру по следующей траектории: К происхождению ф-ооо.

Падение с определенного расстояния г Происходит за конечное время, равное 1 / ш I / M2 ^ 9 / M2 НН \ я ~ ^ + э 3. Добавьте небольшое количество добавки к потенциальной энергии, U = —os / г 6U (g), траектория конечного движения больше не может быть закрыта и сдвигается на небольшое значение угла каждый раз, когда перигелий траектории вращается 6ph. Определите 6ph случая: а) bU = (3 / g2, b) bXJ = y / g 3. Решения.

Когда r изменяется от GST до rmax и снова до GST, угол равен 6 Он варьируется в зависимости от значения, заданного уравнением (14.10). форма rm axe I ———————————————— — д г м2 Af = “20M Jу2т (Е-U) dr Гт (Чтобы избежать существенно расходящегося интегрального падения). Put Разложите подынтегральное выражение со степенями U = —os / g + bU и 6C7.

Нулевой член расширения дает 27t, член первого порядка дает желаемое смешивание 6ph: «Максимум / 7т \ д ф 2мбр д д / 2 т ф 2 \ ч ^ = w » * • „!” ^ 2 м \ E + -) ~ -V o / Где переход от интеграции через Dr к интеграции через C «Беспрепятственная» траектория движения. Для а) интегрирование (1) легко, 2-й (3ш 2-й (3 f « M2 » Of » (P — невозмущенный параметр эллипса (15.4)). б) если r2bU = у / г, Если вы получаете 1 / г из (15,5), BOSUT2 с БИО 6ph = —- ~ M * = _ a «2»

остая проверка прямым расчетом [vM] + ^ = const. (15.17) На самом деле, его общая производная по времени [м] + ^ Или заменить на M = m [rv]. / • \ /. ч, ав ар (вр) rar （^ vv） -mv ^ rv ‘+ f — p- / p% j Где установлено согласно уравнению движения mv = a r / r3, Вы можете видеть, что это выражение исчезает.

Сохраненный вектор (15.17) направлен вдоль главной оси Это тот же размер, что и ось от фокуса до перигелия. Это легко Если вы считаете значения перигелия, вы можете увидеть все. Интеграл движения (15.17) и интегралы M и E являются уникальными функциями состояния ( Жизнь и скорость) частицы.

В § 50 мы видим, что появление таких дополнительных уникальных интегралов связано с так называемым двигательным вырождением. Задание 1. Найти временную зависимость координат частицы при движении в поле U = -os / g с энергией E = 0 (парабола). Решения. С интегральной Младший доктор т = 2а М -г ~ — 2 т?

Для того, чтобы заменить М; (! + L 2) =? (1 + L2) 2tos 2 В результате мы получаем следующий параметр представления желаемой зависимости. x = | (1-l 2), y = t- Параметр r \ выполняет значение от -su до + oo. 2. Интегрировать уравнение движения цены в цену (X ral field u = ——, a> 0. Грамм 2 Решения.

Используя формулы (14.6) и (14.7), выберите соответствующий источник (положите, E * Pn) π, ηM2 1 I (2 2m > 0, -> a- = ^] ^ _ ^ _ cos ^ 1-_ ч M 1/2 т E (2т б) если E> 0, — <a- = \ ———— sh (p \ ———- 1 в) Если E <0, — <a- = \ ———! ch f4 / ———- 1 7 2т г В 2ша-М 2 Г В М 2 Все три случая 1 т t = — \ — \ Er2 ——- h os. E y 2 V 2 t В случае б) и в) частицы «падают» к центру по следующей траектории: К происхождению ф-ооо.

Смотрите также:

Решение задач по физике

Приведенная масса в физике	Распад частиц в физике
Движение в центральном поле в физике	Упругие столкновения частиц в физике

Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.