Оглавление:
Кинематика точки
Рассмотрим движение материальной точки М по отношению к системе ортогональных осей Oxyz. Геометрическое место последовательных положений точки в этой системе назовем траекторией точки. Положение точки в пространстве можно задать ее координатами х, у, z, которые при движении материальной точки будут меняться в зависимости от времени, так что 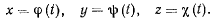
Выписанные уравнения определяют з а к он движения материальной точки и представляют собой параметрические уравнения траектории точки. В непрерывном движении материальной точки будем рассматривать функции 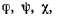 непрерывные вместе со своими производными первого и второго порядков. Рассматривая два близких положения материальной точки М и М) соответствующие моментам времени
непрерывные вместе со своими производными первого и второго порядков. Рассматривая два близких положения материальной точки М и М) соответствующие моментам времени 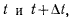 вектор
вектор 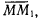 соединяющий эти точки, будем называть вектором перемещения точки за промежуток времени
соединяющий эти точки, будем называть вектором перемещения точки за промежуток времени 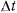 (рис. 26). Обозначая через
(рис. 26). Обозначая через 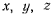 координаты точки М в момент t, а через
координаты точки М в момент t, а через 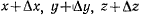 в момент для координат вектора перемещения получим значения
в момент для координат вектора перемещения получим значения 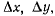
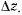 Отношение вектора перемещения ко времени перемещения назовем средней скоростью точки за время
Отношение вектора перемещения ко времени перемещения назовем средней скоростью точки за время 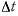
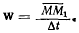
Направление вектора средней скорости точки совпадает с направлением вектора перемещения точки. Предел этого отношения при 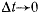 назовем истинной скоростью точки
назовем истинной скоростью точки
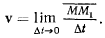
Секущая 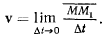 при
при 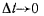 займет предельное положение, совпадающее с положением касательной к кривой в точке М. Вектор средней скорости точки имеет проекции на оси координат
займет предельное положение, совпадающее с положением касательной к кривой в точке М. Вектор средней скорости точки имеет проекции на оси координат 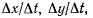 Проекции истинной скорости определяются соотношениями
Проекции истинной скорости определяются соотношениями
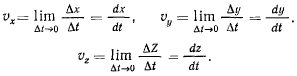
Отсюда следует, что проекции вектора скорости являются первыми производными от координат точки по времени. Производная от радиус-вектора точки. Положение движущейся материальной точки можно определить вектором 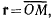 изменяющимся с течением времени по величине и по направлению относительно некоторой системы осей
изменяющимся с течением времени по величине и по направлению относительно некоторой системы осей 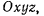 который будем называть радиус-вектором точки (рис. 26). Вектор перемещения точки можно представить через значение радиус-вектора точки в моменты
который будем называть радиус-вектором точки (рис. 26). Вектор перемещения точки можно представить через значение радиус-вектора точки в моменты 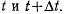
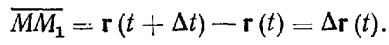
Для средней скорости точки получим теперь выражение
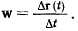
Для истинной же скорости — предел этого отношения 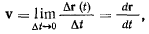
таким образом, скорость точки может быть определена как производная от радиус-вектора точки по времени. Величину скорости точки можно выразить через ее проекции на ортогональные оси координат. 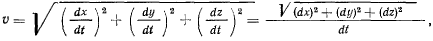
или
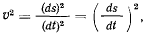
где 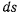 дифференциал дуги траектории точки. Выбрав определенным образом положительное направление отсчета дуги, можно определить, что при возрастании s производная
дифференциал дуги траектории точки. Выбрав определенным образом положительное направление отсчета дуги, можно определить, что при возрастании s производная 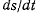 будет положительной. Если условиться, что скорость v положительна в направлении возрастания дуги s, то
будет положительной. Если условиться, что скорость v положительна в направлении возрастания дуги s, то
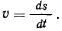
Наиболее простым среди всех возможных движений точки является такое движение, при котором в любой момент времени выполняется условие
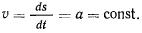
Такое движение будем называть равномерным. Перепишем последнее уравнение в виде Ползун В приводится в движение нитью, наматывающейся
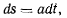
после интегрирования отсюда получим
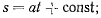
последнее равенство представляет собой закон изменения пути со временем.
Пример:
Точка  совершает движение в плоскости
совершает движение в плоскости 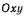 по закону
по закону 
где 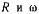 постоянные величины. Определить траекторию и скорость точки.
постоянные величины. Определить траекторию и скорость точки.
Решение:
Уравнение траектории задано в параметрическом виде. Исключив отсюда время 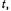 получим
получим
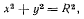
т. е. траекторией точки является окружность радиуса R. Проекции скорости получим, дифференцируя уравнения, определяющие координаты точки как функции времени 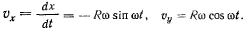
Отсюда величина скорости
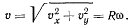
Пример:
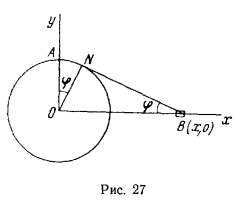
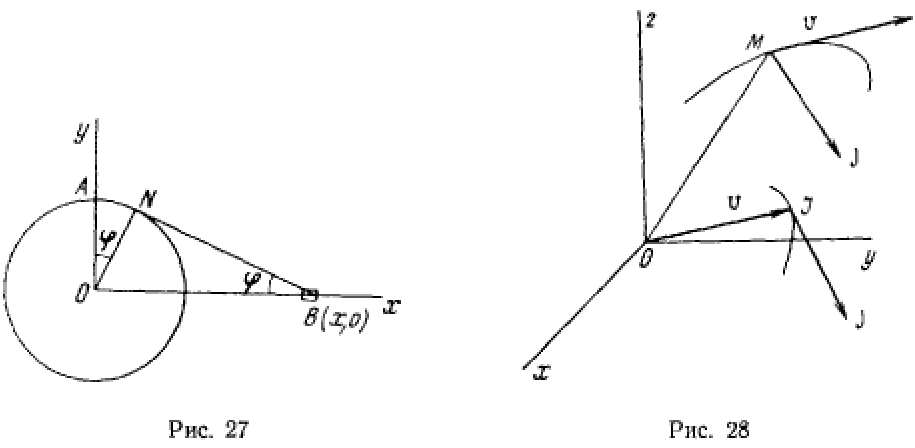
Ползун В приводится в движение нитью, наматывающейся на шкив радиуса 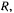 вращающийся с угловой скоростью
вращающийся с угловой скоростью 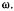 Найти скорость ползуна как функцию расстояния
Найти скорость ползуна как функцию расстояния 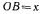 (рис. 27).
(рис. 27).
Решение:
Через неподвижную точку А нить проходит со скоростью 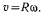 С такой же скоростью изменяется длина отрезка нити
С такой же скоростью изменяется длина отрезка нити 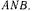 Обозначив длину этого отрезка через
Обозначив длину этого отрезка через 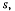 получим
получим
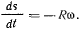
С другой стороны,
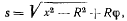
где 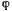 определяется из соотношения
определяется из соотношения
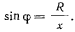
Дифференцируя тождество (а), получим
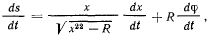
где  определяется из условия
определяется из условия
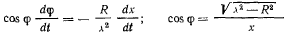
Подставляя 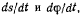 будем иметь
будем иметь
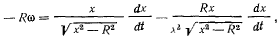
откуда следует
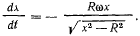
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Ускорение точки |
| Скорость и ускорение точки в полярных координатах |
| Относительное движение материальной точки |
| Принцип Даламбера |
