Оглавление:



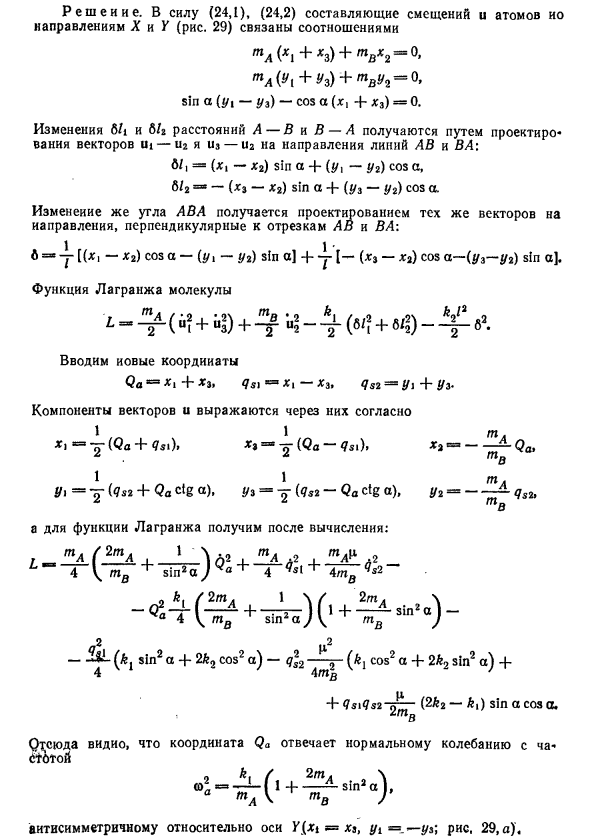


Колебания молекул в физике
- Молекулярная вибрация. При работе с системой взаимодействующих частиц Когда они не расположены друг в друге, но во внешнем поле, не все его степени свободы по существу колеблются. Типичным примером такой системы является молекула. В дополнение к движению, Представляет колебания атомов вокруг положения равновесия в молекуле, и вся молекула может быть переведена и повернута. 3 степени за перевод Свободы.
Так как вращательных степеней свободы столько, сколько в общем случае, 3n степеней свободы p-атома Вся молекула Zn-6 поддерживает колебательное движение. Исключение составляют молекулы, в которых все атомы расположены вдоль прямой линии.
поэтому в этом случае есть только две степени вращения Людмила Фирмаль
Говорить о вращении вокруг этой линии не имеет смысла, , Есть Zn-5. При решении механических задач молекулярных колебаний С самого начала рекомендуется исключить из рассмотрения поступательные и вращательные степени свободы.
Чтобы исключить поступательные движения, необходимо учитывать Сделайте полный импульс молекулы равным нулю. Это условие означает неподвижность центра инерции молекулы, Это выражается как инвариантность последних трех координат.
- Введите m = gao + ua (gao — радиус-вектор положения стационарного равновесия a-го атома, ua — отклонение от этой позиции) и укажите условие. ‘Y jT la T a = C на st EE ^ TPa Ga0 В форме Ничего себе! fflgUg = 0- (24,1) Чтобы исключить молекулярное вращение, Общий момент импульса равен нулю.
Поскольку моменты не являются производными по времени от координатных функций, условия их исчезновения, как правило, Другими словами, это выражается как нулевой эквивалент такой функции. один Единственное исключение — небольшие вариации.
и проигнорируем малые величины второго порядка относительно смещения Людмила Фирмаль
Фактически, если мы снова установим m = ga0 + ua ua, мы можем выразить момент импульса молекулы в виде m = ^ m a [rava] «y ^ m a [ra0ua] = ^ ma [ra0ua]. Следовательно, условие исчезновения в этом приближении может быть выражено как: 5 ^ m [ra0ua] = 0 (24,2) (Источник может быть выбран произвольно.)
Можно классифицировать нормальные молекулярные колебания Основываясь на природе движения атома внутри атома, исходя из соображений симметрии расположения атомов Состояние равновесия. Внутримолекулярное. Для этой цели существует общий метод, основанный на использовании теории групп. Он введен в другом томе этого курса х).
Рассмотрим здесь Просто несколько основных примеров. Если все n атомов молекулы находятся в одной плоскости, Вы можете различить нормальные колебания, составляющие атомы в этой плоскости, и нормальные колебания, при которых атомы удаляются с плоскости. Легко определить оба числа.
Планарное движение имеет 2n степеней свободы, две из которых являются поступательными, а одна — вращательными. Обычное число колебаний, которые не удаляют атомы из плоскости, составляет 2n-3. Оставшиеся (3n-6) — (2n-3) = n-3 Степень свободы соответствует предполагаемой вибрации Атом с самолета.
Для линейных молекул можно выделить вертикальное направление Вибрация, которая поддерживает свою линейную форму, и вибрация, которая удаляет атомы из прямой линии.
Поскольку полное движение n частиц вдоль линии соответствует n степеням свободы, одна из них является поступательной, поэтому число колебаний, которые не удаляют атомы, составляет Прямая линия n-1. Общее количество вибраций ст Степень свободы для линейных молекул составляет Zn-5 и 2n-4.
Вибрация, которая удаляет атомы от прямой линии. Однако эти колебания могут выполняться двумя независимыми способами (две плоскости, перпендикулярные друг другу), поэтому этим колебаниям соответствуют только n-2 разных частот. (Через молекулярную ось), по соображениям симметрии Понятно, что каждая пара таких нормальных вибраций имеет Та же частота. Задача 1)
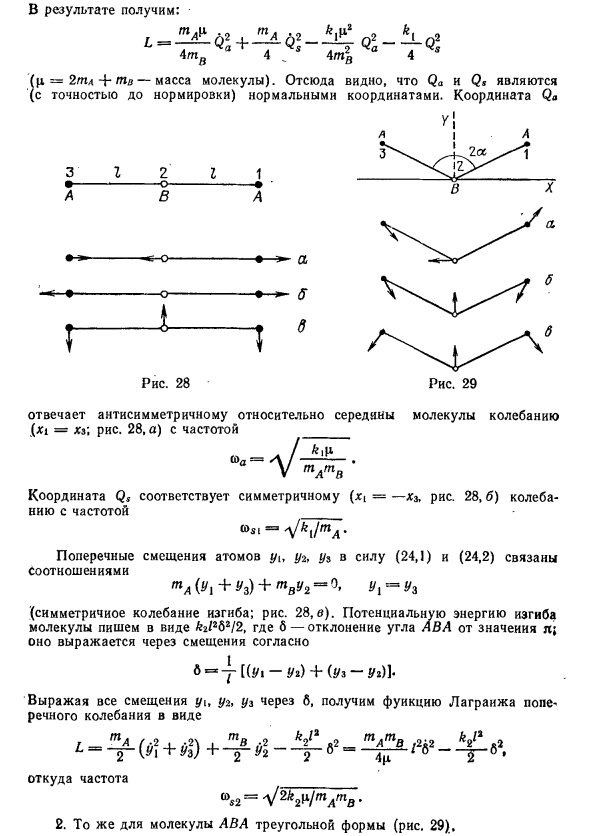
1. Определите частоту колебаний линейной трехатомной молекулы АБК (рис. 28). Предполагается, что потенциальная энергия молекулы зависит только от угловых расстояний ABA A-B и B-Ay. Решения.
Продольные перемещения атомов X1, X2, x3 связаны силой (24.1) В зависимости от отношений hpa (x g + xz) + m bx 2 = 0 Исключает х2 из лагранжевой функции продольного движения молекулы T ГПД. 2 I -2h, t .2 Ки и h 2 | / ch2- | L = — ^ — (^ 1 + X3) + -й номер -XV + (X3-X2) J, Затем введите новые координаты Qoc = x 1 + xs, Qs = x 1-xs. В результате ТГПА ЦД2. GPAH2 & 1 C2 2 & 1 2 L ~ r Qs + ~ u; (Q = 2 ГПа + ТПВ — молекулярная масса).
Это указывает на то, что Qa и Qs являются нормальными координатами (до нормализации). Qa координаты {X \ = xz \ 3 1 2 I, соответствующая вибрации, асимметричной относительно центра молекулы Рис. 28 а) Частота • ° • _ A B A ки \ я —- ^ -o ———— •> «а GPAGPv Координата Qs симметрично соответствует Jb. mu (x \ = —xz) Рис. 28 5)
Частота колебаний ———- ^ ———— J in Игрушка Ох … = [К рисунку. Фигура 28 V ГПД Боковые смещения атомов yy, y2 и kn из-за (24.1) и (24.2) связаны соотношением. GPA (y1 + узлы) + GPVU2 = 0, Y1 = Uz, (Симметричная изгибная вибрация; рис. 28 в).
Описывает потенциальную энергию изгиба молекулы в виде Л2Z262 / 2. Где 6 — отклонение от угла ABA Значение 7 т; 6 = y [(y / 1-2 / 2) + (kn-Y2)]. Выражение всех смещений 2/1, 2/2, 2/3 до 6 дает лагранжеву функцию поперечной вибрации в виде t TPA, .2, 2 \, GPv .2 ^ 2 ^ 2 s2 TP ATP B -.2ё2 & 2 ^ <-2 b = — (y1 + yy) + ^ ry2- ^ r b = ^ q G1 & ~ ^ G & ‘ Откуда берется частота Ws2 = \ ———- • V mAmB 2.
То же самое верно для треугольных молекул АБК (рис. 29). Решения. Благодаря (24.1), (24.2) компоненты смещения и атомы вдоль направлений X и Y (рис. 29) связаны соотношениями ГПа (х 1 + Хс) + TPvX 2 = O, ГПа (U1 + узлы) + ГПВУ2 = о, (Yy-Uz) sin os- (xi + xs) cos os = 0
Изменения в 6Zi и 6/2 расстояний A-B и B-A получены путем проектирования в направлении линий AB и B A от векторов ui-U2 и -U2. 6 Z1 = (x \ -X2) sin os + (t / i-Y2) cos os, L2 = ~ (x3-x2) sin os + (kn-Y2) cos os. Изменение угла ABA можно получить, спроектировав один и тот же вектор в направлении, перпендикулярном сегменту. AB и B A: Ј> = y [(x 1 — x2), потому что os- (y1-y2) sin a] + + y [- (x3-x2) cos os- (kn-y2) sin a].
Лагранжева функция молекулы ГПа (. 2. • 2 . ГПВ. 2 L = — (ui + u3) + -u2- Пожалуйста, введите новые координаты Q a = x 1 + Xs, 2 * 1 = X! -Xs, qs2 = 2 / i + 2 / 3- Компоненты вектора Xl = ~ (Q a + <? Sl), X3 = \ (Qa ~ qS l), X2 = «Qa, 2 Z 771 дюйм g / 1 = ^ (gS2 + Qa Ctga), 2/3 = -Qa Ctga), 2/2 = qs2 2 2
гпв Функция Лагранжа получается после расчета. L = —Γ ——— б. 2 Qa + —r I a 1 + -j —— Qs2 4 \ tv sin os / 4 4tv 2 & 1 / 2tA, 1 \ L, 2tA. 2 \ -Q a ~ r [——— + -Г-2—) (1 + ———— sm <*) — 4 V TV Sm A / V TV / 2 2 -sin2 a + 2 ^ 2 cos2 a) -g22 ^ 9 (fci cos2 a + 2 ^ 2 sin2 a) + 4 4777 / ^ + qfsi qS2 tg ~~ (2 ^ 2-k i) sin a cos a.
В ом Это показывает, что координата Qa соответствует нормальной вибрации с частотой (L, 2tA. 2 \ 1 N ——— sm os, «APGV 771 в» W в Асимметричный относительно оси y (xi = x3, yi = —yz) Рис. 29 а). Координаты qs i и qs2 вместе соответствуют двум колебаниям (симметричным относительно оси y: x \ = —x3, y \ = uz].
Рис. 29 b и c), cusi, частота, определяемая как квадратный корень квадратного корня из cvS2 (по si2) Характеристическое уравнение w4-2cr & 1 — / -1 2H-m-A— — co2 s \ oc. М-2 — ^ — 2- — 1. H-2-t-A— —. s2m Mos, I-2-c — & — 1 — & — 2- = n0. ИМА В ТВ / 771л В ТВ / J ТВТА При 2 ° C = n все эти частоты соответствуют частотам, указанным в задаче 1. 3. То же самое относится и к линейным асимметричным молекулам ABC (рисунок 30).
Решения. Продольные (x) и боковые (y) атомные смещения связаны соотношением 3/2 2 l \ 1. • о tAH 1 + швж2 + tps% s = 0, C V A hPAy 1 + тву2 + цуз = 0, р 3Q mAliyi = tcb- Потенциальная энергия растяжения и изгиба может быть описана следующим образом. ^ / ^ 7 ^ 1 ^ 1 / * 1 ^ Ј2 у№) + у№) + ^ «5 (2 / = Zi + / 2) — Расчет аналогичен расчету, выполненному в задаче 1 Приводит к значению 2 = k212 (II 1 \ 412 ч / ^ 2 771 л
Частота поперечных колебаний и уравнение квадратного уравнения (si2) w4-w1 [/! , (- + -) + / О; (- + -)] + — = „ L V777l t in ‘\ t in t s’ -I t A T P vgp s Частота поперечных колебаний и уравнение квадратного уравнения (si2) w4-w1 [/! , (- + -) + / О; (- + -)] + — = „ L V777l t in ‘\ t in t s’ -I t A T P vgp s Для частоты сил tuj2 ДВА продольных вибрации.
Смотрите также:
| Вынужденные колебания в физике | Затухающие колебания в физике |
| Колебания систем со многими степенями свободы | Вынужденные колебания при наличии трения |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.
