Оглавление:
Задание: Исследование абсолютной и условной сходимости знакочередующихся рядов.
Цель: формирование умения исследовать знакочередующиеся ряды на абсолютную и условную сходимость.
Задание для самостоятельной внеаудиторной работы:
40.1. Запомните определение знакочередующегося ряда. Выучите формулировку достаточного признака сходимости знакочередующегося ряда — признака Лейбница. Постарайтесь освоить алгоритм работы с этим признаком.
40.2. Используя признак Лейбница, исследуйте на сходимость знакочередующиеся ряды:
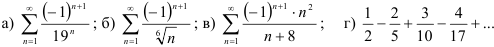
40.3. Выучите, какой знакочередующийся ряд называется абсолютно сходящимся. Выясните, какова техника исследования ряда на абсолютную сходимость. Внимательно изучите пример такого исследования.
40.4. Выучите, какой знакочередующийся ряд называется условно сходящимся. Проанализируйте, в чём заключается отличие абсолютно сходящегося ряда от условно сходящегося. Выясните, какой алгоритм позволяет исследовать характер сходимости
знакочередующегося ряда. На примере ряда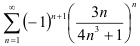 
постарайтесь его освоить.
40.5. Определите, какие из следующих знакочередующихся рядов сходятся абсолютно, какие — условно, какие — расходятся:
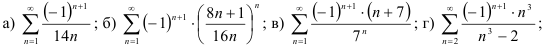
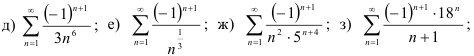
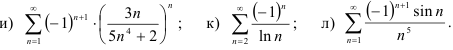
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Ряд называется знакочередующимся, если положительные и отрицательные члены ряда следуют друг за другом поочередно:
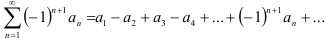, где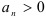 
для всех 
.
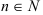Для знакочередующихся рядов имеет место достаточный признак сходимости — признак Лейбница.
Признак Лейбница. Если последовательность абсолютных величин членов знакочередующегося ряда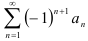 
монотонно убывает 
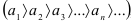, и общий член ряда стремится к нулю 
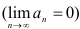, то знакочередующийся ряд сходится.
Доказывать сходимость знакочередующегося ряда 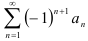по признаку Лейбница удобно с помощью алгоритма:
- выписать модуль общего члена исходного ряда
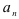; - найти
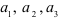и проверить выполнение неравенств: 
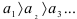; - найти предел общего члена ряда
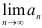и убедиться в том, что он равен нулю.
Пример 1.
Исследуйте сходимость знакочередующегося ряда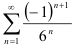 
с помощью признака Лейбница.
Решение:
Для исследования сходимости знакочередующегося ряда по признаку Лейбница воспользуемся алгоритмом.
- Выпишем модуль общего члена исходного ряда:
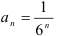. - Найдём :
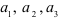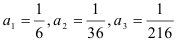. Неравенства 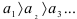справедливы, т.к. 
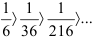(тем самым первое условие признака Лейбница выполняется). - Найдём
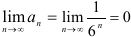(второе условие признака Лейбница выполняется).
Следовательно, но признаку Лейбница знакочередующийся ряд 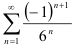сходится.
Ответ: 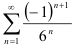сходится.
Знакочередующийся ряд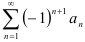 
называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов 
.
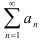Заметим по определению, что исследование абсолютной сходимости знакочередующегося ряда фактически сводится к исследованию сходимости положительного ряда. Таким образом, для этой цели можно использовать все признаки сходимости положительных рядов.
Пример 2.
Докажите, что знакочередующийся ряд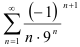 
абсолютно сходится.
Доказательство. Составим ряд из модулей членов данного ряда: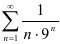 
.
Исследуем полученный положительный ряд на сходимость с помощью признака Даламбера по алгоритму.
- Найдём
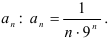
- Найдём
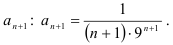
- Найдём
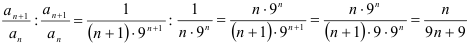. - Найдём
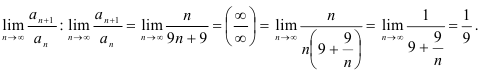
В итоге,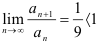 
. Значит, по признаку Даламбера ряд 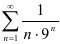сходится. Следовательно, по определению, знакочередующийся ряд 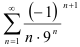абсолютно сходится, что и требовалось доказать.
Для абсолютно сходящихся рядов справедливо утверждение: если знакочередующийся ряд абсолютно сходится, то он и просто сходится.
Знакочередующийся ряд 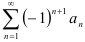называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов 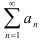расходится.
Пример 3.
Докажите, что знакочередующийся ряд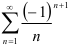 
условно сходится.
Доказательство. Исследуем сходимость знакочередующегося ряда с помощью признака Лейбница по алгоритму.
- Выпишем модуль общего члена исходного ряда:
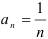. - Найдём :
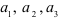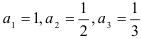. Неравенства 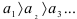справедливы, т.к. 
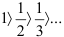(первое условие признака Лейбница выполнено). - Найдём
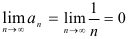(второе условие признака Лейбница выполнено).
Следовательно, по признаку Лейбница знакочередующийся ряд 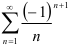сходится.
Исследуем сходимость ряда, составленного из модулей членов данного знакочередующегося ряда. Ряд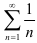 
является расходящимся гармоническим рядом. Следовательно, по определению, знакочередующийся ряд 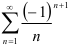условно сходится, что и требовалось доказать.
Для определения характера сходимости знакочередующегося ряда
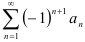удобно использовать следующий алгоритм:
- составить ряд из модулей членов данного ряда: ;
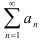- исследовать положительный ряд 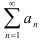на сходимость;
- если ряд 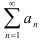сходится, то знакочередующийся ряд 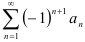абсолютно сходится (следовательно, и просто сходится);
- если ряд 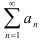расходится, то исследовать знакочередующийся ряд 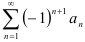на сходимость;
- сделать вывод об условной сходимости знакочередующегося ряда .
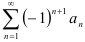Пример 4.
Исследуйте характер сходимости знакочередующегося ряда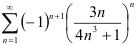 
.
Решение:
Для исследования характера сходимости знакочередующегося ряда 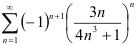воспользуемся алгоритмом.
1. Составим ряд из модулей членов данного ряда: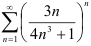 
.
2. Исследуем полученный положительный ряд 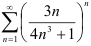на сходимость с помощью признака Коши, т.к. общий член ряда представляет собой 
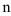-ую степень выражения 
:
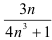- выпишем
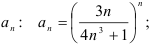
- найдём
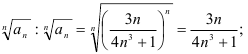
- найдём
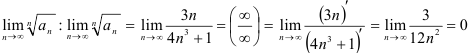(при раскрытии неопределенности 
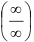использовали правило Лопиталя). В итоге, 
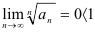. Значит, по признаку Коши ряд 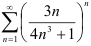сходится.
3. Поскольку ряд 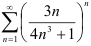сходится, то по определению, знакочередующийся ряд 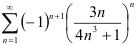абсолютно сходится (следовательно, и просто сходится).
Ответ: 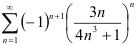абсолютно сходится.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
