Оглавление:
Задание: Нахождение неопределённых интегралов методом подстановки.
Цель: формирование умения находить неопределённые интегралы методом подстановки.
Задание для самостоятельной внеаудиторной работы:
23.1. Разберите, какие функции можно считать «некоторыми сложными функциям», какова техника нахождения интеграла от «некоторых сложных функций». Проанализируйте, в чём заключается сущность метода замены переменной в неопределённом интеграле (метода подстановки). Разберите алгоритм нахождения неопределённого интеграла методом подстановки. Ответьте на контрольные вопросы:
- Какие функции мы будем считать «некоторыми сложными»?
- Какова техника нахождения интегралов от «некоторых сложных функций»?
- В чём заключается сущность метода интегрирования подстановкой?
23.2. Найдите интегралы от «некоторых сложных функций»:

23.3. Найдите интегралы методом замены переменной (подстановки):
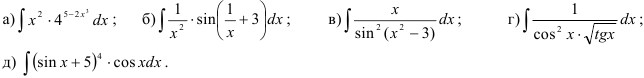
23.4. Найдите интегралы:
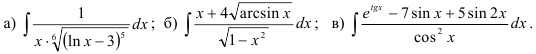
Методические указания no выполнению работы:
Некоторыми сложными функциями будем считать функции вида 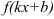 , где
, где 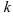 и
и 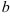 любые действительные числа,
любые действительные числа, 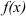 — функция, от которой существует табличный интеграл.
— функция, от которой существует табличный интеграл.
Так, 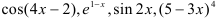 — примеры некоторых сложных функций. В аргументе этих функций переменная х находится только в первой степени!
— примеры некоторых сложных функций. В аргументе этих функций переменная х находится только в первой степени!
Для нахождения интеграла от некоторых сложных функций будем использовать формулу:
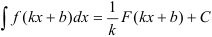 или применять следующий алгоритм.
или применять следующий алгоритм.
- Проанализируйте, к какому табличному интегралу можно свести данный интеграл.
- Вместо
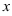 в табличный интеграл подставьте выражение
в табличный интеграл подставьте выражение 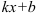 из исходного интеграла.
из исходного интеграла. - В правую часть введите дополнительный множитель
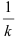 , где
, где 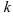 — коэффициент перед
— коэффициент перед 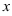 .
.
Рассмотрим нахождение интеграла от некоторых сложных функций на примерах.
Пример 1.
Найдите 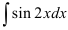 .
.
Решение:
Видим, что под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 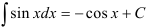 .
.
В нашем примере в качестве аргумента выступает угол 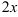 . Выделим коэффициент
. Выделим коэффициент 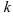 , стоящий перед
, стоящий перед 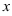 :
: 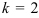 , следовательно, в правую часть мы должны ввести множитель
, следовательно, в правую часть мы должны ввести множитель 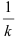 , то есть
, то есть 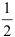 . Тогда получим, что
. Тогда получим, что 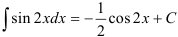 .
.
Ответ: 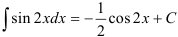 .
.
Пример 2.
Найдите 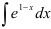 .
.
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 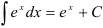 .
.
В примере в качестве аргумента выступает выражение  . Выделим коэффициент
. Выделим коэффициент 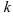 , стоящий перед
, стоящий перед 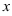 :
: 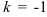 , следовательно, в правую часть вводим множитель (-1). Тогда получим, что
, следовательно, в правую часть вводим множитель (-1). Тогда получим, что 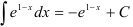 .
.
Ответ: 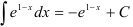 .
.
Пример 3.
Найдите 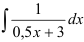 .
.
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом  .
.
В примере в качестве аргумента выступает выражение 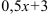 . Выделим коэффициент
. Выделим коэффициент 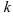 , стоящий перед
, стоящий перед 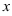 :
: 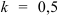 , следовательно, в правую часть введём множитель 1:0,5=2. Тогда получим, что
, следовательно, в правую часть введём множитель 1:0,5=2. Тогда получим, что 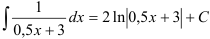 .
.
Ответ: 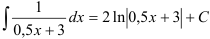 .
.
Пример 4.
Найдите 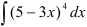 .
.
Решение:
Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом 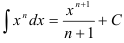 .
.
В примере в качестве аргумента выступает выражение  . Выделим коэффициент
. Выделим коэффициент 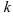 , стоящий перед
, стоящий перед 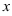 :
: 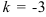 , следовательно, в правую часть введём множитель (-1/3). Тогда получим, что
, следовательно, в правую часть введём множитель (-1/3). Тогда получим, что 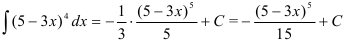 .
.
Ответ: 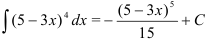 .
.
Сущность метода интегрирования подстановкой заключается в том, что путем введения новой переменной удаётся свести заданный интеграл к новому интегралу, который является табличным.
В основе метода подстановки лежит формула замены переменной в неопределенном интеграле: 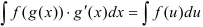 .
.
Для нахождения неопределенного интеграла методом подстановки (замены переменной) целесообразно использовать следующий алгоритм:
- Введите новую переменную
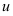 таким образом, чтобы под знаком интеграла стояла функция, содержащая
таким образом, чтобы под знаком интеграла стояла функция, содержащая 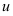 (от этой функции должен существовать табличный интеграл), и производная
(от этой функции должен существовать табличный интеграл), и производная 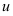 .
. - Найдите
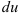 по формуле:
по формуле: 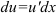 .
. - Выразите
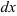 через
через 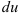 (при этом помните, что если множитель в одной части формулы находился в числителе, то в другую часть он перейдет в знаменатель и наоборот: если множитель находился в знаменателе, то в другую часть он «перейдёт» в числитель).
(при этом помните, что если множитель в одной части формулы находился в числителе, то в другую часть он перейдет в знаменатель и наоборот: если множитель находился в знаменателе, то в другую часть он «перейдёт» в числитель). - Подставьте
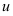 и
и 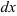 в исходный интеграл. Если подстановка выполнена верно, то произойдет сокращение одинаковых множителей и интеграл сведется к табличному относительно переменной
в исходный интеграл. Если подстановка выполнена верно, то произойдет сокращение одинаковых множителей и интеграл сведется к табличному относительно переменной 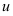 :
: 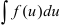 .
. - Пользуясь таблицей неопределённых интегралов, возьмите полученный интеграл с переменной
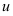 .
. - Перейдите от переменной интегрирования
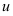 к исходной переменной
к исходной переменной 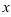 .
.
Рассмотрим применение метода подстановки на конкретных примерах.
Пример 5.
Найдите 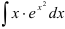 .
.
Решение:
1. Выполним подстановку  с целью прийти к интегралу от функции
с целью прийти к интегралу от функции 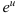 .
.
2. Найдем 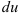 по формуле
по формуле 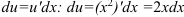 .
.
3. Выразим 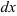 из выражения пункта 2
из выражения пункта 2 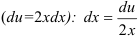 .
.
4. Подставим 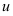 и
и 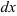 в исходный интеграл:
в исходный интеграл: 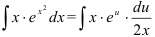 . Видим, что переменную
. Видим, что переменную 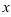 можно сократить и прийти к интегралу относительно переменной
можно сократить и прийти к интегралу относительно переменной 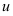 :
:  .
.
5. Для нахождения полученного интеграла константу 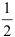 вынесем за знак интеграла:
вынесем за знак интеграла: 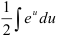 . По таблице неопределенных интегралов находим, что
. По таблице неопределенных интегралов находим, что 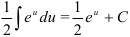 .
.
6. Поскольку 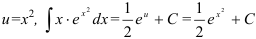 .
.
Ответ: 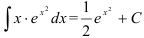 .
.
Пример 6.
Найдите  .
.
Решение:
1. Выполним подстановку 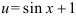 . Тогда под знаком интеграла будет стоять функция от
. Тогда под знаком интеграла будет стоять функция от 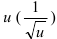 и производная
и производная 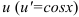 .
.
2. Найдем 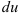 по формуле
по формуле 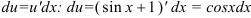 .
.
3. Выразим 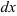 из выражения пункта 2
из выражения пункта 2 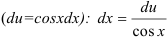 .
.
4. Подставим 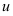 и
и 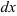 в исходный интеграл:
в исходный интеграл: 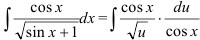 . Видим, что
. Видим, что  можно сократить и прийти к интегралу относительно переменной
можно сократить и прийти к интегралу относительно переменной 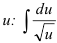 .
.
5. По таблице неопределенных интегралов находим, что 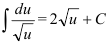 .
.
6. Поскольку 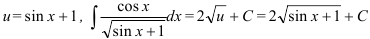 .
.
Ответ: 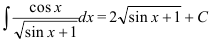 .
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
