Оглавление:
Задание: Решение дифференциальных уравнений второго порядка.
Цель: формирование умений решать дифференциальные уравнения второго порядка: простейшие, линейные однородные с постоянными коэффициентами.
Задание для самостоятельной внеаудиторной работы:
49.1. Какие дифференциальные уравнения называют простейшими второго порядка? Какова техника их решения?
49.2. Решите простейшие дифференциальные уравнения второго порядка:
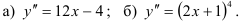
49.3. Найдите частное решение простейших дифференциальных уравнений второго порядка:
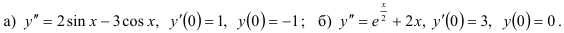
49.4. Какие дифференциальные уравнения называют линейными однородными (ЛОДУ) второго порядка с постоянными коэффициентами? Какова техника их решения?
49.5. Решите ЛОДУ II порядка с постоянными коэффициентами:
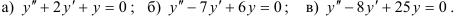
49.6. Решите дифференциальные уравнения второго порядка:
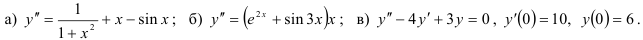
Методические указания по выполнению работы:
Выделяют следующие виды дифференциальных уравнении второго порядка:
1. Простейшие дифференциальные уравнения второго порядка — уравнения вида: 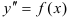 .
.
Метод решения, двукратное интегрирование по переменной 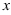 .
.
Пример 1.
Найдите решение дифференциального уравнения 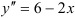 .
.
Решение:
Поскольку перед нами простейшее дифференциальное уравнение второго порядка, найдем сначала 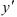 по формуле:
по формуле: 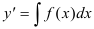 .
.
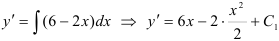 или
или 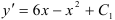 , где
, где 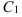 — константа.
— константа.
Для нахождения искомой функции 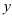 найдем интеграл от
найдем интеграл от 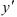 по переменной
по переменной 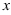 :
:
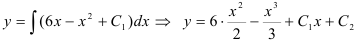 или
или 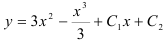 , где
, где 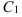 и
и  — константы.
— константы.
Полученная функция является общим решением дифференциального уравнения 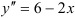 .
.
Ответ: 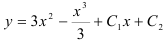 .
.
Обратите внимание, что общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные 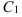 и
и  .
.
Для нахождения решения задачи Коши можно использовать следующий алгоритм:
- Найдите
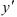 по формуле:
по формуле: 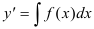 .
. - Воспользовавшись первым начальным условием (
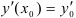 ), найдите значение константы
), найдите значение константы 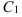 и подставьте его в функцию
и подставьте его в функцию 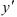 .
. - Найдите функцию
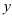 , взяв интеграл от
, взяв интеграл от 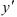 по переменной
по переменной 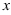 .
. - Воспользовавшись вторым начальным условием (
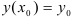 ), найдите значение константы
), найдите значение константы  и подставьте его в функцию
и подставьте его в функцию 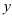 . Полученная функция
. Полученная функция 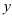 будет являться частным решением исходного дифференциального уравнения.
будет являться частным решением исходного дифференциального уравнения.
Пример 2.
Найдите решение задачи Коши: 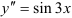 , если при
, если при 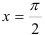 ,
, 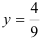 и
и 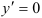 .
.
Решение:
1. Найдем 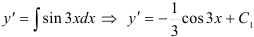 .
.
2. Воспользуемся первым начальным условием: 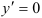 при
при 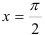 . Подставим эти числа в функцию
. Подставим эти числа в функцию 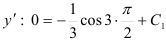 . Поскольку
. Поскольку 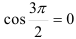 , получим, что
, получим, что 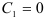 .
.
Подставим найденное значение 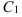 в функцию
в функцию 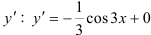 или
или 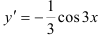 .
.
3. Найдем функцию 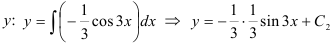 или
или 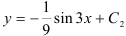 .
.
4. Воспользуемся вторым начальным условием: 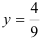 при
при 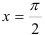 . Подставим эти числа в функцию
. Подставим эти числа в функцию 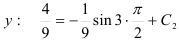 . Поскольку
. Поскольку
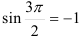 , получим:
, получим: 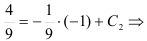
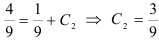 или
или 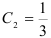 .
.
Найденное значение константы  подставим в функцию
подставим в функцию 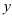 :
: 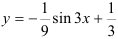 . Полученная функция является частным решением исходного дифференциального уравнения
. Полученная функция является частным решением исходного дифференциального уравнения 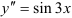 при заданных начальных условиях.
при заданных начальных условиях.
Ответ: 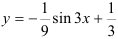 .
.
2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами — уравнение вида 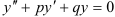 , где
, где 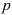 и
и 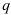 — постоянные величины.
— постоянные величины.
Для нахождения решения дифференциальных уравнений такого вида будем составлять характеристическое уравнение: 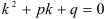 , где
, где 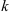 — некоторая новая переменная. Характеристическое уравнение является квадратным относительно
— некоторая новая переменная. Характеристическое уравнение является квадратным относительно 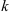 .
.
В зависимости от числа и вида корней данного характеристического уравнения, решение исходного дифференциального уравнения можно представить в виде таблицы 49.1:
Таблица 49.1
Решение линейных однородных дифференциальных уравнений второго порядка с постоянным и коэффициентами
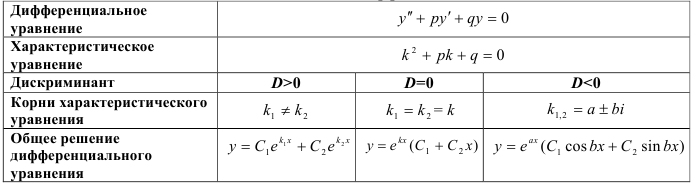
Рассмотрим решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами на конкретных примерах.
Пример 3.
Решите дифференциальное уравнение: 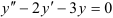 .
.
Решение:
Составим характеристическое уравнение 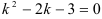 . Найдем его корни.
. Найдем его корни. 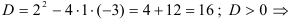 существуют два различных корня
существуют два различных корня 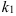 и
и 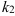 .
.
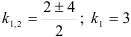 или
или 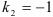 .
.
Тогда, пользуясь таблицей 49.1, находим общее решение дифференциального уравнения по формуле 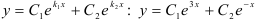 .
.
Ответ: 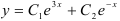 .
.
Пример 4.
Решите дифференциальное уравнение: 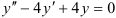 .
.
Решение:
Составим характеристическое уравнение 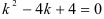 . Найдем его корни.
. Найдем его корни. 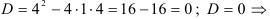 существуют два равных корня
существуют два равных корня 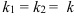 .
.
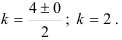
Тогда, пользуясь таблицей 49.1, находим общее решение дифференциального уравнения по формуле 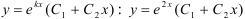 .
.
Ответ: 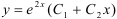 .
.
Пример 5.
Решите дифференциальное уравнение: 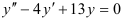 .
.
Решите дифференциальное уравнение: 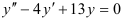 .
.
Решение:
Составим характеристическое уравнение 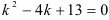 . Найдем его корни.
. Найдем его корни. 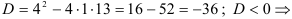 существуют два комплексных корня
существуют два комплексных корня 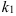 и
и 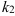 .
.
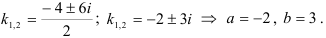
Тогда, пользуясь таблицей 49.1, находим общее решение дифференциального уравнения по формуле 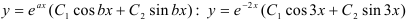 .
.
Ответ: 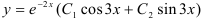 .
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
