Контрольная работа К2.
Круглая пластина радиуса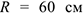 
вращается вокруг неподвижной оси, проходящей через точку 
перпендикулярно плоскости пластины по закону 
. Положительное направление отсчета угла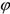 
показано на рис. К2 стрелкой. Ось вращения расположена на расстоянии 
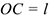от центра пластины. По дуге окружности радиуса 
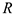движется и точка 
по закону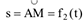 
. Начало относительного движения в точке 
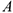, положительное направление отсчета 
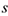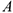— от к .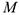
Дано:
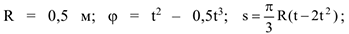
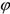( — в радианах, 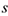— в метрах, 
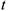— в секундах).
Определить: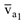 
и 
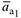в момент времени 
.
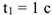Решение
1 Рассмотрим движение точки 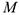как сложное, считая её движение по дуге окружности относительным, а вращение плиты — переносным движением. Исследование задачи проведем в следующей последовательности.
Найдем положение точки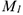 
в относительном движении и определим угловую скорость и угловое ускорение плиты при 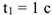. Имеем дуговую координату
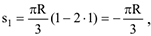
который соответствует центральный угол
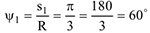
Знак (-) свидетельствует о том, что дуговую координату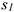 
или центральный угол 
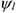в момент времени 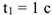. Необходимо отложить против хода часовой стрелки, т.е. точка 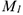находится слева от точки 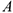. Здесь и далее индекс «1» при символах означает, что соответствующая величина вычислена при .
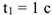Имеем угловую скорость и угловое ускорение плиты:
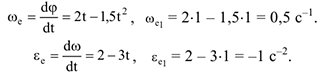
Направления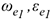 
соответственно показаны на рис. К2
2 Определение абсолютной скорости. В момент времени 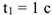по формуле (3.31) имеем:
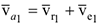
При определении относительной скорости мысленно остановим переносное движение.
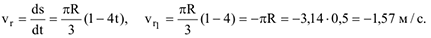
Знак (-) показывает, что вектор 
направлен в сторону отрицательного отсчета дуговой координаты .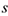
При определении переносной скорости мысленно остановим относительное движение, т.е. будем считать, что точка находится в положении 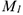, жестко связана с плитой и вместе с плитой вращается вокруг точки 
.
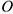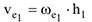
где
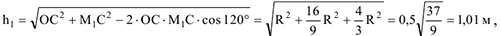
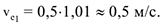
Модуль абсолютной скорости в момент времени 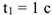найдем по теореме косинусов:
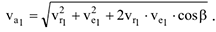
Угол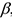 
в свою очередь, определим по теореме синусов:
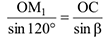
Отсюда
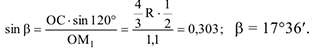
Тогда
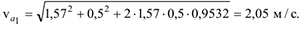
3 Определение абсолютного ускорения. В момент времени 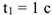по формуле (3.34) имеем:
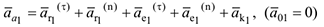
Найдем касательную составляющую относительного ускорения:
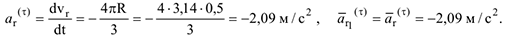
Касательное ускорение есть постоянная величина и, как показывает знак (-), направлено в противоположную сторону 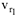. Нормальное ускорение относительного движения равно
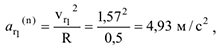
которое направлено к центру кривизны относительной траектории, т.е. к центру окружности радиуса .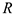
Касательная и нормальная составляющие ускорения переносного движения точки определяются соответственно по формулам:
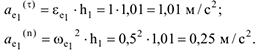
Причем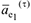 
направлено по касательной к траектории переносного движения, к дуге окружности радиуса 
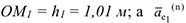— к центру этой окружности, т.е. к точке 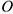. Вычислим модуль Кориолисова ускорения:
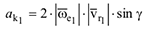
где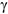 
— угол между векторам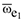и 
и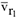 
. Из рис. К2 очевидно, что 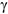= 90°. Таким образом
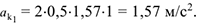
Направление ускорения Кориолиса определяется по правилу Жуковского. При этом будем учитывать, что 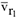лежит в плоскости, перпендикулярной 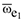т.е. в плоскости диска. Тогда поворотом вектора 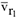на 90° по ходу переносного вращения получим направление Кориолисова ускорения (рис. К2).
Модуль абсолютного ускорения получаем следующим образом. С началом в точке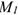 
выбираем абсолютную систему координат. Учитывая, что все векторы полученных выше ускорений лежат в одной в плоскости, в плоскости диска, достаточно выбрать двумерную систему координат. Причем оси этой системы рационально направить по взаимоперпендикулярным векторам слагаемых ускорений. Поэтому ось 
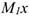направляем к центру окружности радиуса 
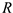, по направлению векторов 
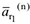и 
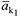, ось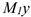 
— по касательной к этой окружности, по направлению вектора 
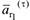. Затем все слагаемые ускорения спроектируем на эти оси. Вычислив алгебраические суммы одноименных проекций векторов ускорений, определим соответствующие проекции искомого вектора 
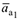на эти оси.
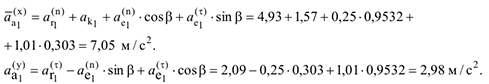
Модуль направления вектора абсолютного ускорения точки определяется по формулам:
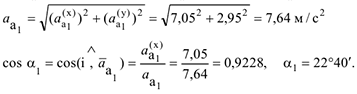
Таким образом, абсолютная скорость точк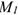и при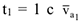 
имеет модуль 
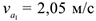и образует угол с осью 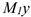(с касательной)
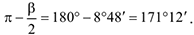
При этом абсолютное ускорение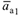 
имеет модуль 
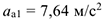и образует с осью 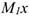угол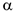 
.
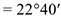