Оглавление:
Последовательностью называют пронумерованный ряд чисел. Нумерация при этом может начинаться с любого целого числа (чаще всего с единицы) и заканчиваться каким-либо натуральным числом. Например:
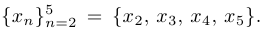
В этом случае мы говорим о конечной последовательности. Чаще в курсе математического анализа рассматриваются бесконечные последовательности. При этом нумерация, как правило, начинается с 1. В этом случае мы определяем последовательность как функцию, заданную на множестве натуральных чисел, и записываем 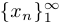 . Иногда для краткости мы будем писать просто
. Иногда для краткости мы будем писать просто 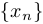 или
или 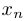 . При этом обычно этой функции соответствует функция
. При этом обычно этой функции соответствует функция 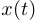 , определенная при
, определенная при 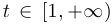 такая, что
такая, что 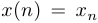 при
при 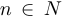 . Такую функцию мы будем называть накрывающей. Однако в ряде случаев такую накрывающую функцию найти непросто, особенно если последовательность задана рекуррентным способом, то есть если каждый ее член определяется через предыдущие.
. Такую функцию мы будем называть накрывающей. Однако в ряде случаев такую накрывающую функцию найти непросто, особенно если последовательность задана рекуррентным способом, то есть если каждый ее член определяется через предыдущие.
Простейшие свойства последовательностей.
Основным в курсе математического анализа является определение предела последовательности, однако прежде чем к нему переходить, дадим еще несколько интуитивно понятных и естественных определений.
Последовательность называется возрастающей, если 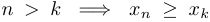 ; строго возрастающей, если
; строго возрастающей, если 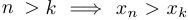 ; (соответственно определяются убывающая и строго убывающая последовательности);
; (соответственно определяются убывающая и строго убывающая последовательности);
- монотонной, если она убывающая или возрастающая;
- ограниченной сверху, если
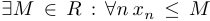 . Аналогично определяется ограниченная снизу последовательность.
. Аналогично определяется ограниченная снизу последовательность. 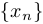 называется просто ограниченной, если она ограничена и сверху, и снизу;
называется просто ограниченной, если она ограничена и сверху, и снизу; - положительной (отрицательной), если
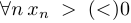 , знакопостоянной, если она положительна или отрицательна, знакопеременной, если она содержит как положительные, так и отрицательные члены, и знакочередующейся, если знаки ее членов чередуются.
, знакопостоянной, если она положительна или отрицательна, знакопеременной, если она содержит как положительные, так и отрицательные члены, и знакочередующейся, если знаки ее членов чередуются.
Иногда указанные термины употребляются и в том случае, когда соответствующее свойство выполняется не всегда, а лишь начиная с некоторого номера.
Пример 1.
a) 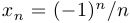 — знакочередующаяся, ограниченная последовательность:
— знакочередующаяся, ограниченная последовательность:
b) 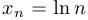 — положительная (при
— положительная (при 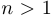 ), строго возрастающая неограниченная последовательность;
), строго возрастающая неограниченная последовательность;
c) 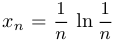 — неположительная ограниченная последовательность.
— неположительная ограниченная последовательность.
Упр. 1. Опишите свойства последовательностей, изображенных ниже на рисунках  .
.
Пример 2.
Доказать, что последовательность 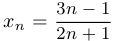 монотонна и ограничена.
монотонна и ограничена.
Решение:
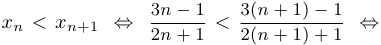
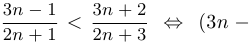
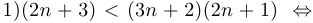
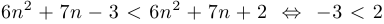 , что очевидно. Таким образом, мы доказали, что последовательность
, что очевидно. Таким образом, мы доказали, что последовательность 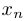 монотонно возрастает. Докажем, что последовательность ограничена сверху (тот факт, что она ограничена снизу, очевиден: все члены последовательности положительные числа, и, следовательно,
монотонно возрастает. Докажем, что последовательность ограничена сверху (тот факт, что она ограничена снизу, очевиден: все члены последовательности положительные числа, и, следовательно, 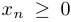 ). Оценим сверху дробь, определяющую
). Оценим сверху дробь, определяющую 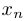 :
: 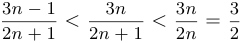 . Утверждение доказано.
. Утверждение доказано.
Пример 3.
Доказать, что последовательность 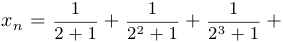
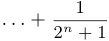 ограничена.
ограничена.
Решение. 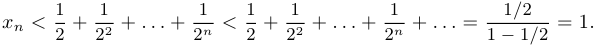
Пример 4.
Доказать, что последовательность 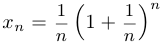 ограничена.
ограничена.
Решение 1-е.
Оценка снизу очевидна 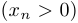 . Чтобы оценить последовательность сверху, запишем
. Чтобы оценить последовательность сверху, запишем 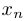 в виде
в виде 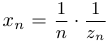 , где
, где 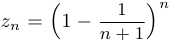 . Используя неравенство Бернулли, получим, что
. Используя неравенство Бернулли, получим, что 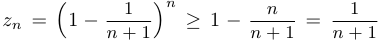 . Следовательно,
. Следовательно, 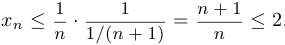 .
.
Решение 2-е.
Докажем сначала, что 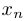 убывает. Для этого рассмотрим отношение
убывает. Для этого рассмотрим отношение 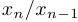 и покажем, что оно меньше 1.
и покажем, что оно меньше 1.
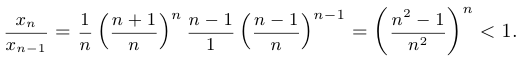
Пример 5.
Доказать, что последовательность 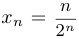 монотонно убывает и ограничена.
монотонно убывает и ограничена.
Решение:
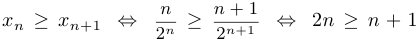 . Таким образом, монотонность доказана, причем, начиная с
. Таким образом, монотонность доказана, причем, начиная с 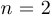 , монотонность строгая. Поскольку
, монотонность строгая. Поскольку 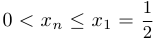 , то ограниченность очевидна.
, то ограниченность очевидна.
Другой способ доказательства монотонности и ограниченности состоит в том, что для изучаемой последовательности 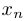 рассматривается соответствующая накрывающая функция
рассматривается соответствующая накрывающая функция 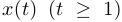 и с помощью производной показывается ее монотонность и ограниченность. Например, если
и с помощью производной показывается ее монотонность и ограниченность. Например, если 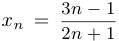 , то
, то 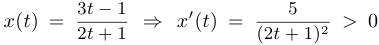 . При использовании этого способа мы несколько забегаем вперед, однако «порочного круга» (утверждение
. При использовании этого способа мы несколько забегаем вперед, однако «порочного круга» (утверждение 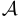 доказывается с помощью
доказывается с помощью 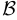 , которое, в свою очередь, доказывается с использованием
, которое, в свою очередь, доказывается с использованием 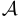 ) мы в данном случае можем не опасаться, поскольку доказательство условия монотонности функции не использует свойств последовательностей.
) мы в данном случае можем не опасаться, поскольку доказательство условия монотонности функции не использует свойств последовательностей.
Предел последовательности.
Число 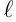 называется пределом последовательности
называется пределом последовательности 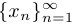 , если
, если
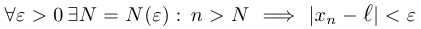
(для любого положительного эпсилон существует число 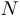 такое, что если номер
такое, что если номер 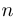 больше
больше 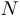 , то
, то 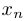 отличается по модулю от
отличается по модулю от 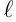 меньше чем на эпсилон).
меньше чем на эпсилон).
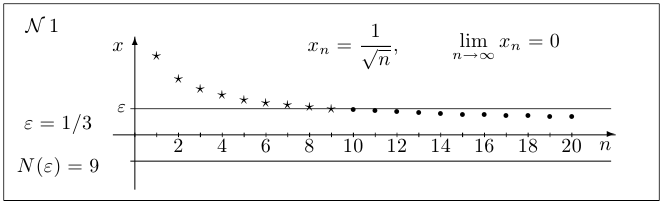
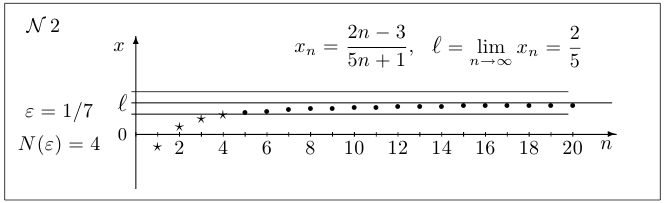
Пример 6.
 . По заданному числу
. По заданному числу  найти число
найти число  .
.
Решение:
Сначала выдвигаем гипотезу, что 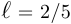 . Неравенство
. Неравенство 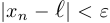 выглядит так:
выглядит так:
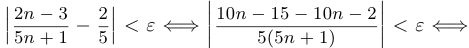
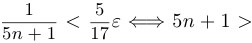
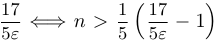 . Заметим, что нам не обязательно иметь точное значение
. Заметим, что нам не обязательно иметь точное значение 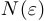 . Достаточно получить такой номер, начиная с которого неравенство выполняется наверняка. В данном случае можно взять, например,
. Достаточно получить такой номер, начиная с которого неравенство выполняется наверняка. В данном случае можно взять, например, 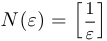 .
.
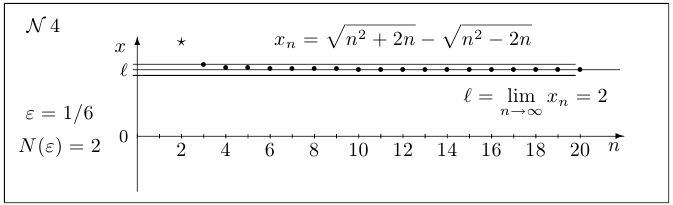
Упр. 2. Для следующих последовательностей укажите по 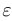 номер
номер 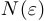 , начиная с которого выполняется неравенство
, начиная с которого выполняется неравенство 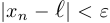 .
.
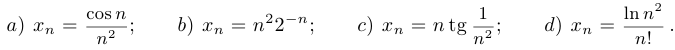
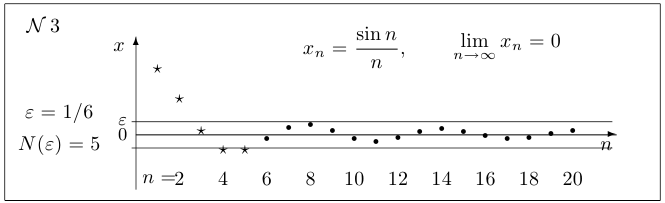
Если последовательность 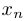 имеет предел, то говорят, что она сходится, или является сходящейся. Если этим пределом является число
имеет предел, то говорят, что она сходится, или является сходящейся. Если этим пределом является число 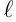 , то пишут
, то пишут 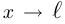 при
при  .
.
Утверждение. Любая сходящаяся последовательность ограничена.
Теорема об арифметических операциях с пределами. Если последовательности 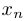 и
и 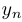 являются сходящимися, то последовательности
являются сходящимися, то последовательности 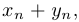
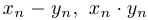 также являются сходящимися, причем:
также являются сходящимися, причем:
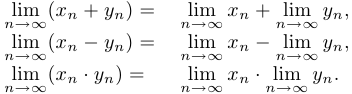
Все то же самое верно и для отношения 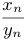 , но при дополнительном предположении, что
, но при дополнительном предположении, что 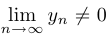 .
.
Бесконечно малые и бесконечно большие величины. Последовательность 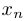 называется бесконечно малой (б.м.), если
называется бесконечно малой (б.м.), если 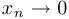 при
при  .
.
Утверждение. Произведение б.м. последовательности на ограниченную есть б.м. величина.
Определение. Говорят, что последовательность 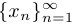 стремится к бесконечности (и пишут
стремится к бесконечности (и пишут 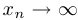 ), если
), если
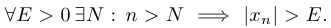
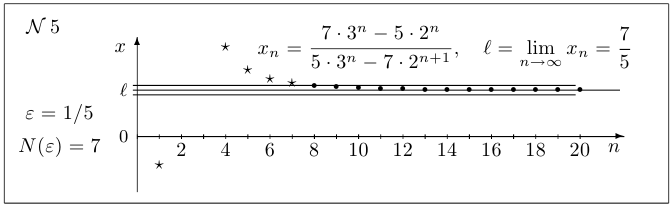
Если выполняется условие 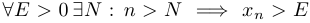 , то говорят, что последовательность стремится к плюс бесконечности (
, то говорят, что последовательность стремится к плюс бесконечности (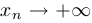 ).
).
Если выполняется условие 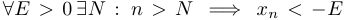 , то говорят, что последовательность стремится к минус бесконечности (
, то говорят, что последовательность стремится к минус бесконечности (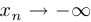 ).
).
Последовательность 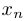 называется бесконечно большой (б.б.), если
называется бесконечно большой (б.б.), если 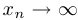 при
при  .
.
Утверждение. Произведение б.м. последовательности на ограниченную есть б.м. последовательность. Если ограниченную последовательность разделить на б.б., то получится б.м. последовательность.
Утверждение. Любая сходящаяся последовательность может быть представлена как сумма постоянной (равной пределу) и б.м. последовательности.
Примеры бесконечно малых последовательностей:
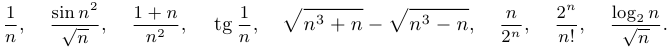
Примеры бесконечно больших последовательностей:
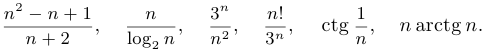
Дробно-рациональной функцией называется функция вида 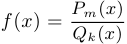 , где
, где
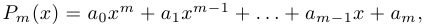

Теорема о дробно-рациональной функции:
если 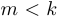 , то
, то 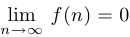 ;
;
если 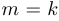 , то
, то 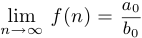 ;
;
если 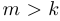 , то
, то 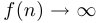 .
.
Пример 7.
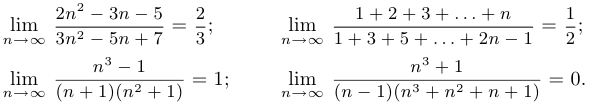
Теорема о переходе к пределу в неравенстве. Если последовательности 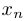 и
и 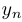 являются сходящимися и
являются сходящимися и 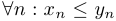 , то
, то 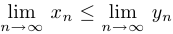 .
.
Теорема о сжатой последовательности. Пусть три последовательности 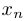 ,
, 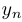 и
и 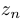 при любом
при любом 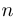 удовлетворяют неравенствам
удовлетворяют неравенствам 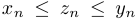 . Если последовательности
. Если последовательности 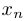 и
и 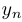 являются сходящимися и при этом
являются сходящимися и при этом 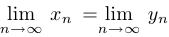 , то последовательность
, то последовательность 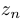 также имеет предел и
также имеет предел и 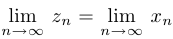 .
.
Теорема об ограниченной и монотонной последовательности. Если последовательность монотонна и ограничена, то она имеет предел.
Теперь перейдем к разделу, содержащему важное применение этой теоремы.
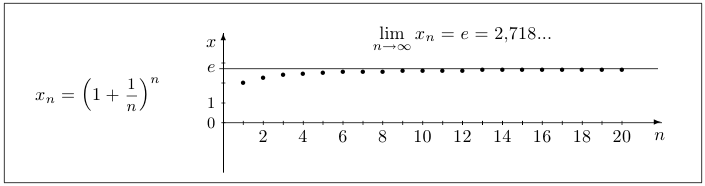
Число 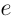 . Для определения числа
. Для определения числа 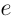 нам понадобятся две последовательности:
нам понадобятся две последовательности:
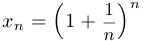 и
и 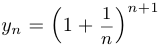 .
.
Утверждение. Последовательность 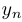 является строго убывающей.
является строго убывающей.
Доказательство. Строгое убывание означает, что при 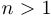 выполняется неравенство
выполняется неравенство 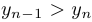 . Это эквивалентно неравенству
. Это эквивалентно неравенству
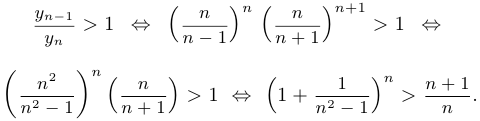
Обозначим через 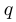 дробь
дробь 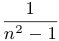 . Применяя неравенство Бернулли, получим
. Применяя неравенство Бернулли, получим 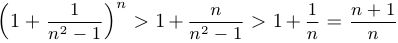 , поскольку
, поскольку 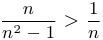 . Утверждение доказано.
. Утверждение доказано.
Поскольку последовательность 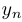 ограничена снизу (все ее члены положительны), то она имеет предел. Этот предел является положительным числом и обозначается через
ограничена снизу (все ее члены положительны), то она имеет предел. Этот предел является положительным числом и обозначается через 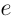 .
.
Упр. 3. Доказать, что последовательность 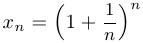 является строго возрастающей.
является строго возрастающей.
Нетрудно заметить, что для любого 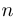 выполняются неравенства
выполняются неравенства 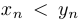 , поскольку
, поскольку  . Таким образом,
. Таким образом, 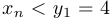 .
.
Мы доказали, что обе последовательности 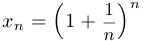 и
и 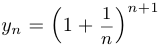 сходятся и имеют один и тот же предел, который и есть число
сходятся и имеют один и тот же предел, который и есть число 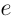 .
.
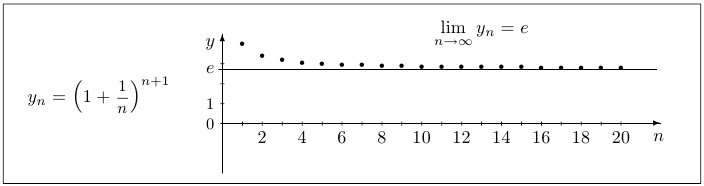
Существует много способов определения числа 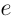 . Например, к этому числу сходится последовательность
. Например, к этому числу сходится последовательность
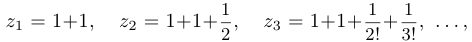
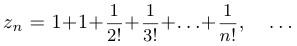
Ниже показаны первые значения последовательностей 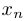 и
и 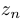 :
:
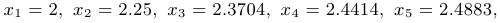
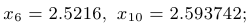
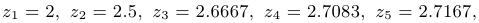
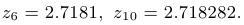
Приближенное значение числа 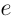 равно
равно 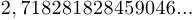
Пример 8.
Доказать, что последовательность 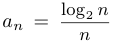 монотонно убывает, начиная с
монотонно убывает, начиная с 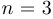 , и ограничена.
, и ограничена.
Решение:
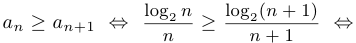
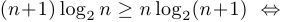
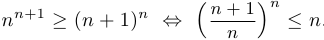 .
.
Последнее неравенство при 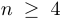 следует из предыдущего утверждения. При
следует из предыдущего утверждения. При 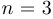 неравенство проверяется непосредственно.
неравенство проверяется непосредственно.
Таким образом, монотонность доказана, причем, начиная с 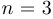 , монотонность строгая.
, монотонность строгая.
Поскольку 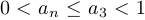 , то ограниченность очевидна.
, то ограниченность очевидна.
Рекуррентные последовательности.
Говорят, что последовательность задается рекуррентным соотношением, если каждый член этой последовательности является заданной функцией предыдущих членов этой же последовательности. При этом для корректного задания последовательности необходимо задать также значения одного или нескольких первых членов этой последовательности.
Примеры:
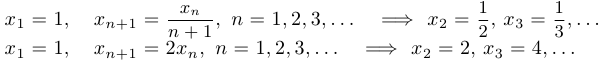
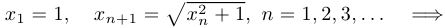
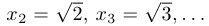
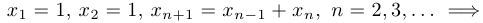
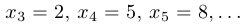
Пример 9.
Доказать, что последовательность, задаваемая начальным условием 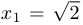 и рекуррентным соотношением
и рекуррентным соотношением 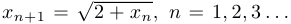 , сходится, и найти ее предел.
, сходится, и найти ее предел.
Решение:
Сначала докажем методом математической индукции, что последовательность ограничена, а именно, что 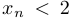 . База индукции очевидна, поскольку
. База индукции очевидна, поскольку 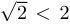 . Предположим теперь, что
. Предположим теперь, что 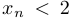 , и докажем, что
, и докажем, что 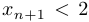 . Имеем, что
. Имеем, что 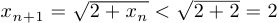 . Утверждение доказано.
. Утверждение доказано.
Теперь докажем, что последовательность 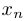 строго возрастает:
строго возрастает: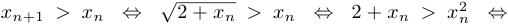
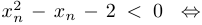
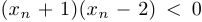 . Поскольку
. Поскольку 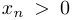 и
и 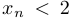 , то последнее неравенство очевидно. Монотонность доказана.
, то последнее неравенство очевидно. Монотонность доказана.
Из теоремы о монотонной ограниченной последовательности следует, что 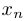 имеет предел. Обозначим этот предел через
имеет предел. Обозначим этот предел через 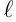 . Поскольку
. Поскольку 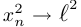 при
при  , то из равенства
, то из равенства 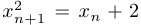 следует, что
следует, что 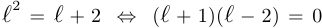 . Поскольку
. Поскольку 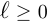 , то
, то 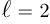 .
.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: метод математической индукции |
| Курсовая работа на тему: элементы комбинаторики |
| Курсовая работа на тему: предел функции |
| Курсовая работа на тему: производная |
