Оглавление:
В начале этой главы мы вернемся к теме «Пределы» и рассмотрим один из самых удобных и популярных способов вычисления пределов.
Теорема (правило) Лопиталя.
Предположим, что функции 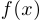 и
и 
1) определены, непрерывны и дифференцируемы в некоторой окрестности точки 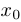 ;
;
2) 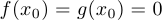 ;
;
3) существует предел  .
.
Тогда существует также и предел 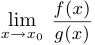 , причем
, причем
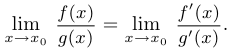
Заметим, что аналогичное утверждение верно и в случае, когда 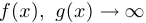 при
при  . Оно называется вторым правилом Лопиталя.
. Оно называется вторым правилом Лопиталя.
Пример 1.
Найти предел 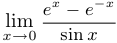 .
.
Решение. В данном случае 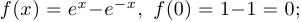
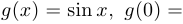
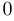 . Таким образом, можно воспользоваться основным правилом Лопиталя.
. Таким образом, можно воспользоваться основным правилом Лопиталя.

Пример 2.
Найти предел 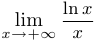 .
.
Решение. В данном случае  при
при 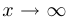 . Таким образом, можно воспользоваться вторым правилом Лопиталя.
. Таким образом, можно воспользоваться вторым правилом Лопиталя.

Пример 3.
Найти предел 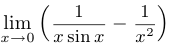 .
.
Решение. После приведения к общему знаменателю заменим множитель 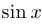 в знаменателе на эквивалентный
в знаменателе на эквивалентный  .
. 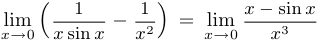 . Теперь можно применить правило Лопиталя, но придется сделать это три раза, чтобы избавиться от неопределенности.
. Теперь можно применить правило Лопиталя, но придется сделать это три раза, чтобы избавиться от неопределенности.
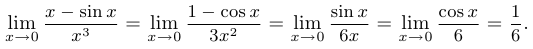
Вторая производная.
Вторая производная не является принципиально новым понятием — это производная от производной. Производная от второй производной называется третьей производной и так далее.
Пример 4.

Пример 5.
Найти 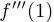 , если
, если 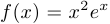 . Дифференцируя поочередно, получим, что
. Дифференцируя поочередно, получим, что 
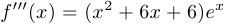 . Подставляя нужное значение аргумента, получим ответ:
. Подставляя нужное значение аргумента, получим ответ:  .
.
Если функции 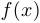 и
и  имеют производную порядка
имеют производную порядка 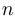 , то для производной произведения справедлива формула Лейбница:
, то для производной произведения справедлива формула Лейбница:

Пример 6.
Найти 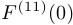 , если
, если  .
.
Решение. Запишем формулу Лейбница: 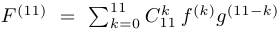 , где
, где 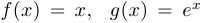 . Поскольку любая производная функции
. Поскольку любая производная функции 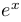 совпадает с ней самой, то
совпадает с ней самой, то 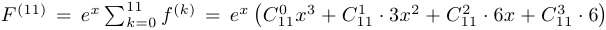 . Подставляя
. Подставляя 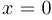 , получим, что
, получим, что 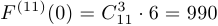 .
.
Пример 7.
Найти  , если
, если 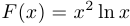 .
.
Решение. Поскольку третья производная функции 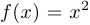 равна нулю, получим, что
равна нулю, получим, что  , где
, где 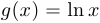 . Тогда
. Тогда
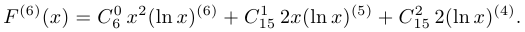
Найдем производные логарифма: 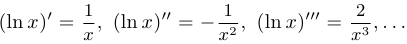

Таким образом, 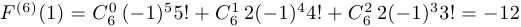 .
.
Выпуклые функции.
В этом разделе мы будем с самого начала предполагать, что рассматриваемые функции определены и непрерывны на некотором промежутке.
Определение 1. Непрерывная функция 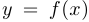 , определенная на промежутке
, определенная на промежутке 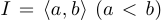 называется выпуклой или выпуклой вниз на этом промежутке, если для любых точек
называется выпуклой или выпуклой вниз на этом промежутке, если для любых точек 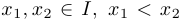 хорда, соединяющая точки
хорда, соединяющая точки 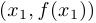 и
и  , лежит выше графика функции на участке
, лежит выше графика функции на участке  . Функция называется вогнутой или выпуклой вверх на этом промежутке, если любая хорда лежит ниже графика.
. Функция называется вогнутой или выпуклой вверх на этом промежутке, если любая хорда лежит ниже графика.
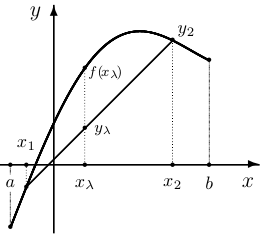
На рисунке справа представлен график функции, выпуклой вверх на отрезке  . Здесь
. Здесь 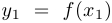 и
и 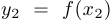 . Множество точек
. Множество точек 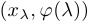 , где
, где 

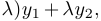
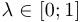 образует отрезок (хорду), соединяющий точки
образует отрезок (хорду), соединяющий точки 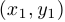 и
и 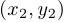 . Условие выпуклости вверх выглядит так:
. Условие выпуклости вверх выглядит так: 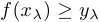 .
.
Определение 2. Функция 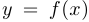 , определенная и непрерывная на промежутке
, определенная и непрерывная на промежутке 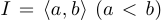 называется выпуклой на этом промежутке, если для любых точек
называется выпуклой на этом промежутке, если для любых точек 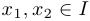 выполняется неравенство
выполняется неравенство 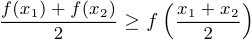 . Если последнее неравенство является строгим для любых точек
. Если последнее неравенство является строгим для любых точек 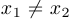 , то функция называется строго выпуклой. Если выполняются неравенства противоположного направления, то функция называется вогнутой или выпуклой вверх.
, то функция называется строго выпуклой. Если выполняются неравенства противоположного направления, то функция называется вогнутой или выпуклой вверх.
Определение 3. Функция 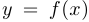 , определенная, непрерывная и дифференцируемая на промежутке
, определенная, непрерывная и дифференцируемая на промежутке 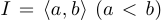 называется выпуклой на этом промежутке, если для любой точки
называется выпуклой на этом промежутке, если для любой точки 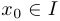 касательная к графику, проведенная в этой точке, лежит выше графика.
касательная к графику, проведенная в этой точке, лежит выше графика.
Теорема об эквивалентности определений выпуклости. На множестве непрерывных на промежутке функций определения 1 и 2 эквивалентны. На множестве дифференцируемых на промежутке функций все три определения эквивалентны.
Критерий выпуклости.
Если функция 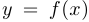 , определенная и непрерывная на промежутке
, определенная и непрерывная на промежутке 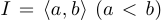 в каждой точке этого промежутка имеет вторую производную, причем
в каждой точке этого промежутка имеет вторую производную, причем 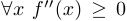 , то функция выпукла. Если неравенство строгое, то функция строго выпукла.
, то функция выпукла. Если неравенство строгое, то функция строго выпукла.
Если 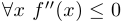 , то функция вогнута.
, то функция вогнута.
Пример 8.
Функции 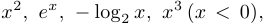
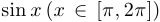 являются выпуклыми.
являются выпуклыми.
Пример 9.
Функции 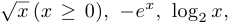
 являются вогнутыми.
являются вогнутыми.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: производная |
| Курсовая работа на тему: монотонность и экстремумы |
| Курсовая работа на тему: графики функций |
| Курсовая работа на тему: кривые, заданные параметрически |
