Оглавление:
Приращение функции, производная и дифференциал. Рассмотрим произвольную функцию 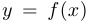 , определенную на некотором множестве
, определенную на некотором множестве 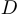 , являющемся подмножеством вещественной оси, и пусть
, являющемся подмножеством вещественной оси, и пусть  и
и 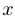 — две точки из области определения функции. Если нас интересует, как меняется значение функции при переходе от
— две точки из области определения функции. Если нас интересует, как меняется значение функции при переходе от  к
к 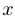 , то мы говорим, что задано приращение аргумента
, то мы говорим, что задано приращение аргумента 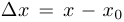 , и рассматриваем приращение функции
, и рассматриваем приращение функции 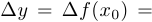
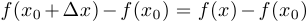 . Заметим, что если
. Заметим, что если  не является изолированной точкой, то при условии, что
не является изолированной точкой, то при условии, что 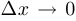 , тот факт, что приращение функции
, тот факт, что приращение функции  является бесконечно малой величиной, означает непрерывность функции в точке
является бесконечно малой величиной, означает непрерывность функции в точке  .
.
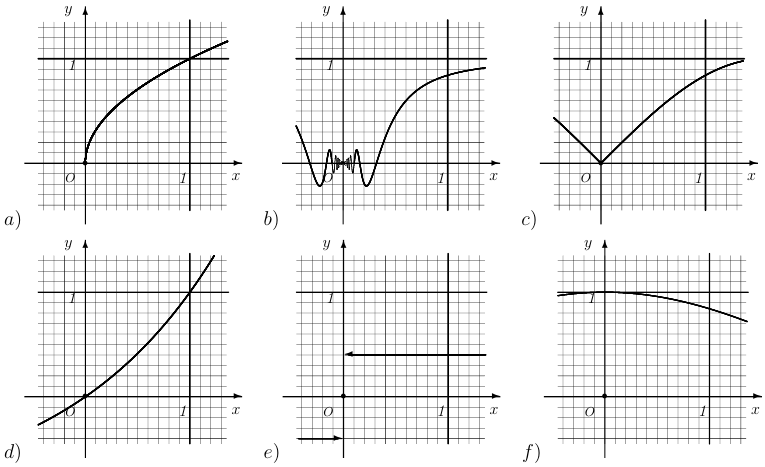
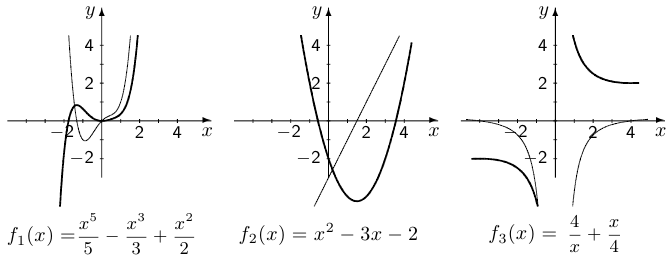
Упр. 1. На рисунках изображены графики шести функций:
1) Сопоставьте каждой функции свой график.
2) Пусть  . В каждом случае, используя рисунок, найдите приближенно приращение функции
. В каждом случае, используя рисунок, найдите приближенно приращение функции  , если
, если 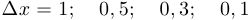 .
.
3) В каком случае величина  не является бесконечно малой при
не является бесконечно малой при 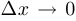 ?
?
Подчеркнем, что если функция не является непрерывной в точке  , то ее приращение в этой точке не является бесконечно малой величиной при стремлении
, то ее приращение в этой точке не является бесконечно малой величиной при стремлении 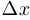 к нулю. Этот случай нам не интересен. Если величина
к нулю. Этот случай нам не интересен. Если величина  является бесконечно малой при
является бесконечно малой при 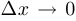 и при этом отношение
и при этом отношение 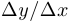 имеет предел, то этот предел называется производной функции
имеет предел, то этот предел называется производной функции 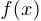 в точке
в точке  и обозначается любым из указанных ниже способов:
и обозначается любым из указанных ниже способов:
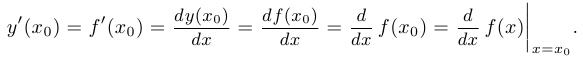
Отметим также, что вместо 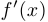 зачастую используется запись
зачастую используется запись 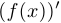 .
.
Если у функции существует производная, то в силу теоремы о выделении линейной части приращение  можно представить в виде
можно представить в виде 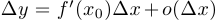 при
при 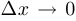 . Сама линейная часть этого представления и называется дифференциалом функции (
. Сама линейная часть этого представления и называется дифференциалом функции (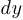 ). Бесконечно малая величина
). Бесконечно малая величина 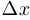 называется дифференциалом переменной
называется дифференциалом переменной 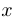 и обозначается через
и обозначается через 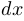 . Таким образом, запись
. Таким образом, запись 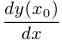 есть просто упрощенное обозначение, сокращение, условная запись того факта, что рассматривается предел
есть просто упрощенное обозначение, сокращение, условная запись того факта, что рассматривается предел 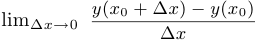 .
.
Повторим основные определения:
1. Дифференциалом переменной 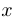 в точке
в точке  называется приращение
называется приращение 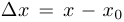 , рассматриваемое как бесконечно малая величина, то есть при
, рассматриваемое как бесконечно малая величина, то есть при 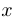 , стремящемся к
, стремящемся к  . Обозначение:
. Обозначение: 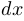 .
.
2. Бесконечно малым приращением функции 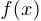 в точке
в точке  называется разность
называется разность 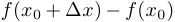 , рассматриваемая при
, рассматриваемая при 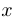 , стремящемся к
, стремящемся к  . Обозначение:
. Обозначение: 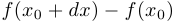 .
.
3. Производной функции 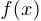 в точке
в точке  называется предел отношения бесконечно малого приращения функции
называется предел отношения бесконечно малого приращения функции 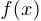 в точке
в точке  к дифференциалу переменной
к дифференциалу переменной 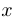 . Обозначение:
. Обозначение: 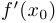 .
.
Таким образом, 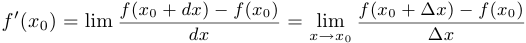 .
.
4. Функция 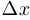 называется дифференцируемой в точке
называется дифференцируемой в точке  , если у нее есть конечная производная в этой точке.
, если у нее есть конечная производная в этой точке.
5. Дифференциалом функции 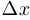 в точке
в точке  называется линейная относительно
называется линейная относительно 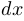 часть в представлении бесконечно малого приращения функции:
часть в представлении бесконечно малого приращения функции:
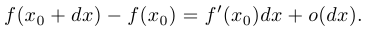
Обозначение: 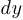 . Другими словами,
. Другими словами, 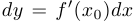 . Заметим, что дифференциал функции определяется только в случае, когда функция в данной точке дифференцируема.
. Заметим, что дифференциал функции определяется только в случае, когда функция в данной точке дифференцируема.
Пример 1.
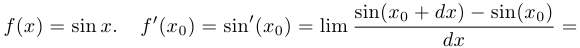
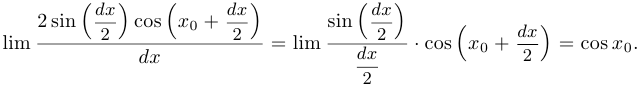
Таким образом, 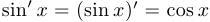 .
.
Пример 2.
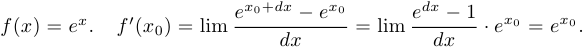
Таким образом, 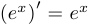 .
.
Пример 3.
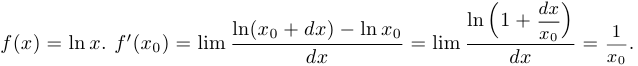
Таким образом, 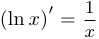 .
.
Упр. 2. Выведите формулы для производных функций: 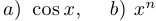 .
.
Получив таблицу производных основных (базисных) элементарных функций, мы можем расширять класс функций, производная которых нам известна, используя основные правила нахождения производных.
Основные правила:
Если 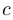 — константа и
— константа и 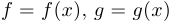 — дифференцируемые функции, то:
— дифференцируемые функции, то:
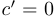 ;
;
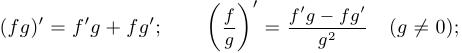
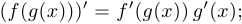
- если
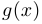 — функция, обратная к
— функция, обратная к 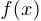 , то
, то 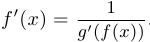 .
.
Пример 4.
Докажем, например, правило для вычисления производной частного. Пусть 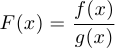 . Тогда:
. Тогда:
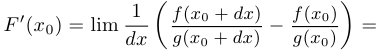
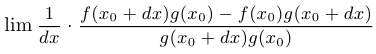
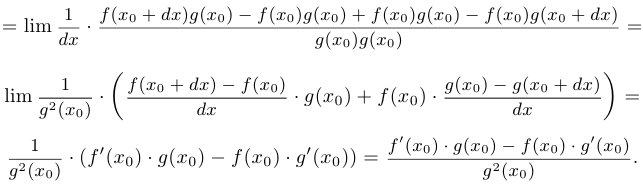
Таким образом, правило доказано.
Заметим, что набор базисных элементарных функций, из которых возможно с помощью допустимых операций получить остальные, невелик, однако, чтобы не заниматься выводом формул для производных, мы предпочитаем сразу предложить таблицу производных, которую необходимо выучить наизусть.
Основные формулы:
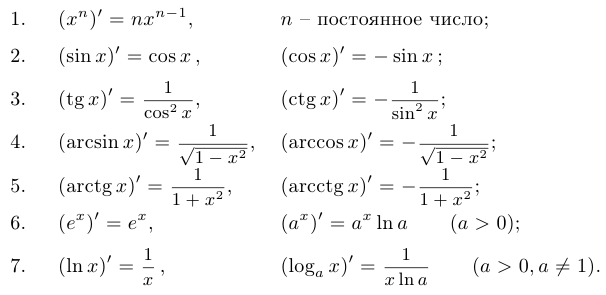
Пример 5.
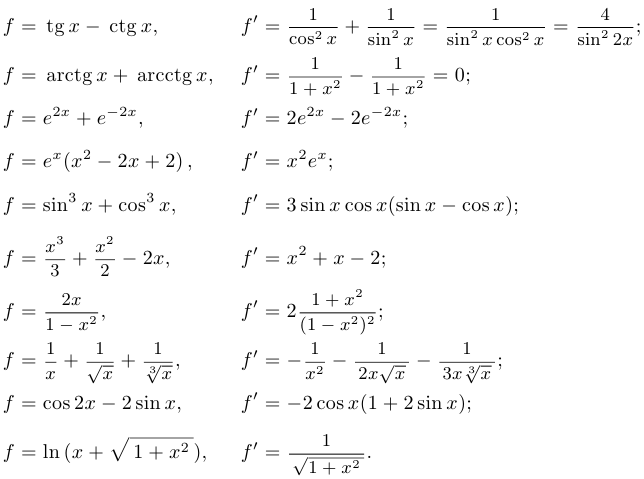
Геометрический смысл производной.
Рассмотрим график функции 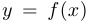 и предположим, что
и предположим, что 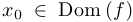 . Пусть
. Пусть 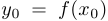 . Рассмотрим также другую точку с координатами
. Рассмотрим также другую точку с координатами 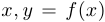 . Обозначим первую точку через
. Обозначим первую точку через 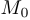 , а вторую через
, а вторую через 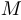 . Прямая, проходящая через любые две точки графика, называется секущей, и в данном случае мы имеем дело с секущей
. Прямая, проходящая через любые две точки графика, называется секущей, и в данном случае мы имеем дело с секущей 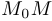 . Угол наклона этой секущей к положительному направлению оси абсцисс нам интересен, поскольку по этому углу можно судить, насколько функция изменилась (увеличилась или уменьшилась) на промежутке
. Угол наклона этой секущей к положительному направлению оси абсцисс нам интересен, поскольку по этому углу можно судить, насколько функция изменилась (увеличилась или уменьшилась) на промежутке 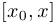 (или
(или 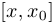 , если
, если 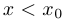 ). На самом деле удобнее следить даже не за углом, а за его тангенсом, который задается формулой
). На самом деле удобнее следить даже не за углом, а за его тангенсом, который задается формулой 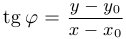 .
.
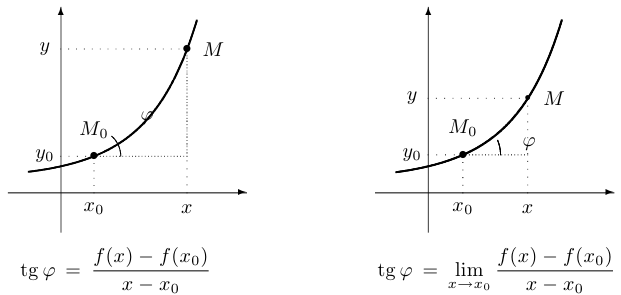
Зафиксируем точку  . При приближении к ней точки
. При приближении к ней точки 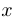 секущая
секущая 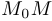 может вести себя по-разному. В «хороших», то есть более привычных нам, ситуациях она приближается к некоторому предельному положению. Это предельное положение называется касательной к функции
может вести себя по-разному. В «хороших», то есть более привычных нам, ситуациях она приближается к некоторому предельному положению. Это предельное положение называется касательной к функции 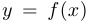 в точке
в точке  . Тангенс угла наклона касательной к положительному направлению оси абсцисс и является производной функции в точке. Таким образом, приходим к классическому определению производной функции
. Тангенс угла наклона касательной к положительному направлению оси абсцисс и является производной функции в точке. Таким образом, приходим к классическому определению производной функции 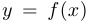 в точке
в точке  :
:
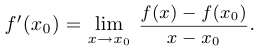
В других обозначениях это выглядит так:
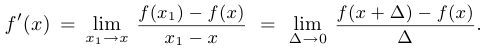
Пример 6.
На каждом из графиков, представляющих указанную функцию, изображен также график производной этой же функции.
Уравнение касательной к графику функции.
Предположим, что прямая 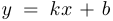 проходит через точку
проходит через точку  , лежащую на графике функции
, лежащую на графике функции  , то есть такую, что
, то есть такую, что 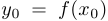 . Это означает, что
. Это означает, что 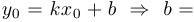
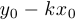 . Следовательно, уравнение имеет вид
. Следовательно, уравнение имеет вид 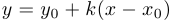 —
—
Коэффициент 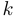 является тангенсом угла наклона прямой к положительному направлению оси абсцисс, и поскольку прямая является касательной, то этот коэффициент равен производной функции в указанной точке, то есть
является тангенсом угла наклона прямой к положительному направлению оси абсцисс, и поскольку прямая является касательной, то этот коэффициент равен производной функции в указанной точке, то есть 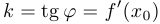 . Таким образом, уравнение касательной имеет следующий вид:
. Таким образом, уравнение касательной имеет следующий вид:
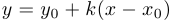 , где
, где 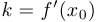 .
.
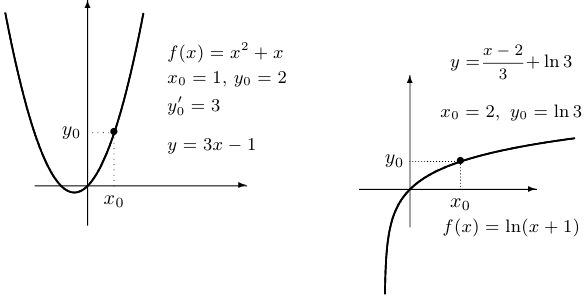
Пример 7.
К графику функции 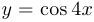 проведена касательная в точке
проведена касательная в точке 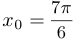 . Найти абсциссу точки пересечения этой касательной с прямой
. Найти абсциссу точки пересечения этой касательной с прямой 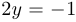 .
.
Решение:
Коэффициент 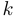 , являющийся тангенсом угла наклона касательной к оси абсцисс, равен
, являющийся тангенсом угла наклона касательной к оси абсцисс, равен 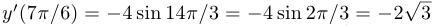 .
.
Уравнение касательной имеет вид 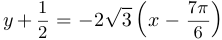 . Таким образом, если
. Таким образом, если 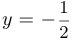 , то
, то 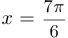 .
.
Ответ: 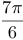 .
.
Пример непрерывной функции, не имеющей производной.
Если функция имеет производную в некоторой точке, то говорят, что она дифференцируема в этой точке. Не всякая непрерывная в точке функция дифференцируема в ней.
Упр. 3. На рисунках изображены графики функций, не имеющих производной в одной или нескольких точках. Укажите, в каких точках производные не определены. В каком случае определены производные «слева» и «справа»? В каких случаях можно говорить о том, что касательные к графику вертикальны?
Существенно сложнее конструируется пример функции, определенной и непрерывной на всей прямой, но не имеющей производной ни в одной точке. Более понятным читателю это построение станет после знакомства с темой «функциональные ряды».
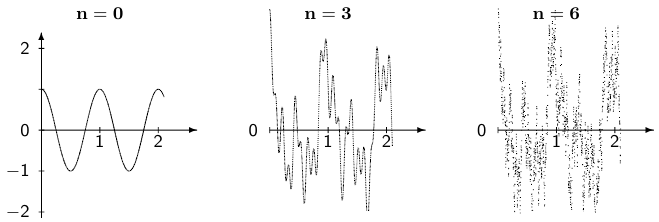
Частичные суммы ряда Вейерштрасса 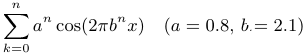
Пример 8.
Построив соответствующие графики, легко убеждаемся, что:
a) функция 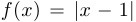 дифференцируема во всех точках, кроме
дифференцируема во всех точках, кроме 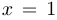 . При этом
. При этом 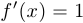 , если
, если 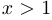 и
и 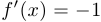 , если
, если 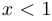 ;
;
b) функция  дифференцируема во всех точках области определения, кроме
дифференцируема во всех точках области определения, кроме 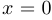 . При этом
. При этом 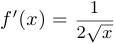 , если
, если 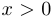 ;
;
с) функция 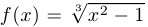 не является дифференцируемой в двух точках:
не является дифференцируемой в двух точках: 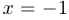 и
и 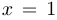 . При этом
. При этом 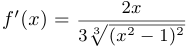 , если
, если 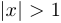 .
.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: числовые последовательности |
| Курсовая работа на тему: предел функции |
| Курсовая работа на тему: монотонность и экстремумы |
| Курсовая работа на тему: правило Лопиталя и выпуклость |
