Задача №12.
Лодку 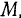 , уносимую течением реки, подтягивают веревкой к точке
, уносимую течением реки, подтягивают веревкой к точке 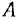 берега. Найти траекторию лодки, принимая последнюю за точку и считая, что скорость
берега. Найти траекторию лодки, принимая последнюю за точку и считая, что скорость 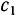 течения реки постоянна по всей ее ширине, скорость наматывания веревки постоянна по величине и равна
течения реки постоянна по всей ее ширине, скорость наматывания веревки постоянна по величине и равна 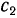 и скорость лодки относительно реки все время направлена вдоль веревки (рис. 16).
и скорость лодки относительно реки все время направлена вдоль веревки (рис. 16).
Решение:
Выберем сначала за подвижную систему координат систему 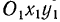 движущуюся поступательно вместе с рекой. В этой системе переносная скорость лодки
движущуюся поступательно вместе с рекой. В этой системе переносная скорость лодки 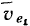 известна по величине и направлению. Она равна скорости течения реки
известна по величине и направлению. Она равна скорости течения реки 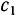 , то есть
, то есть
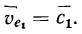
Относительная скорость лодки натравлена вдоль веревки/ но не известна по величине. Исходя из этих данных, мы .можем только сделать заключение о том, что конец вектора абсолютной скорости лежит на прямой 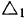 параллельной веревке, но остается неизвестным точное значение абсолютной скорости.
параллельной веревке, но остается неизвестным точное значение абсолютной скорости.
Выберем теперь другую систему подвижных координат 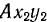 ось Ах2 которой.«проходит все время через лодку. В этой системе координат относительное движение лодки полностью известно. Лодка все время находится на прямой
ось Ах2 которой.«проходит все время через лодку. В этой системе координат относительное движение лодки полностью известно. Лодка все время находится на прямой 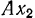 , а ее относительная скорость равна скорости сокращения расстояния
, а ее относительная скорость равна скорости сокращения расстояния 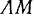 , то есть скорости наматывания веревки
, то есть скорости наматывания веревки 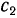 . В переносном движении точка
. В переносном движении точка 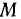 теперь описывает окружность с центром в точке
теперь описывает окружность с центром в точке 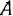 . Переносная скорость лодки направлена по касательной к этой окружности, то есть ортогонально к оси
. Переносная скорость лодки направлена по касательной к этой окружности, то есть ортогонально к оси 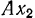 но не известна по величине. Из теоремы о сложении скоростей получаем, что конец вектора абсолютной скорости должен лежать на прямой
но не известна по величине. Из теоремы о сложении скоростей получаем, что конец вектора абсолютной скорости должен лежать на прямой 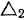 . Мы получили два заключения о решении одной и той же задачи. Конец вектора абсолютной скорости лежит на прямой
. Мы получили два заключения о решении одной и той же задачи. Конец вектора абсолютной скорости лежит на прямой 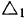 и на прямой
и на прямой 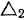 одновременно. Эти прямые пересекаются только в одной точке
одновременно. Эти прямые пересекаются только в одной точке 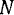 , которая и определяет положение конца вектора абсолютной скорости. Нетрудно теперь видеть, что в системе
, которая и определяет положение конца вектора абсолютной скорости. Нетрудно теперь видеть, что в системе 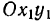 относительная скорость лодки
относительная скорость лодки
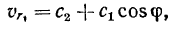
а в системе 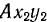 переносная скорость
переносная скорость
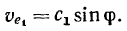
Для определения траектории лодки запишем проекции абсолютной скорости лодки на оси 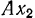 и
и 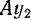 , являющиеся полярными осями:
, являющиеся полярными осями:
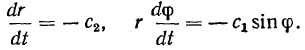
Исключая время, получаем
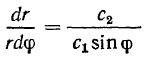
или
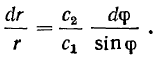
Отсюда имеем
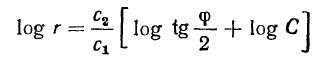
или
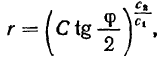
а это и есть конечное уравнение траектории, где 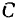 — произвольная постоянная, значение которой определяется начальными условиями
— произвольная постоянная, значение которой определяется начальными условиями
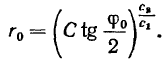
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
