Оглавление:
Логарифмические неравенства с переменными основаниями
Решение логарифмических неравенств с переменными основаниями основано на свойствах логарифмической функции (§ 24, п. 1). Рассмотрим неравенство
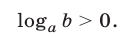
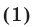
Если верно неравенство (1), то либо (рис. 24.1)
либо (рис. 24.2)
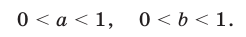
Обратно, из (2) и (3) следует (1), т. е. неравенство (1) равносильно совокупности неравенств (2) и (3). Отсюда следует, что неравенство
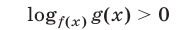
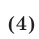
равносильно совокупности двух систем неравентсв
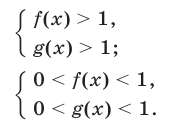
Примеры с решениями
Пример №296.
Решить неравенство
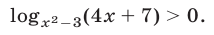
Решение:
Неравенство (7) — это неравенство вида (4), в котором 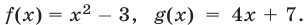 Поэтому неравенство (7) равносильно совокупности систем вида (5) и (6), которые запишутся так:
Поэтому неравенство (7) равносильно совокупности систем вида (5) и (6), которые запишутся так:
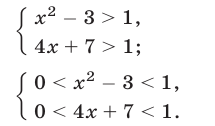

Система (8) равносильна системе
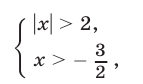
откуда находим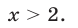
Система (9) равносильна системе
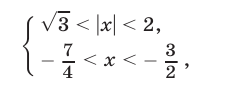
откуда следует, что 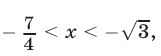 так как
так как 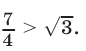
Ответ. 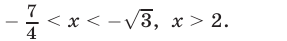
Заметим, что из (2) следует, что 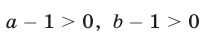 и поэтому
и поэтому
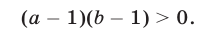
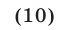
Аналогично, из (3) следует (10). Обратно, если 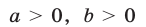 и выполняется условие (10), то либо справедливы неравенства (2), либо являются верными неравенства (3). Таким образом, неравенство (1) равносильно системе неравенств
и выполняется условие (10), то либо справедливы неравенства (2), либо являются верными неравенства (3). Таким образом, неравенство (1) равносильно системе неравенств
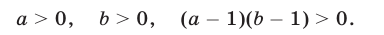
Отсюда следует, что неравенство (4) равносильно системе неравенств
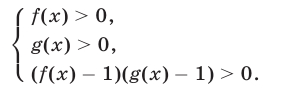
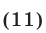
Пример №297.
Решить неравенство
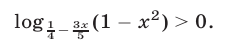
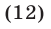
Решение:
Система (11) для неравенства (12) равносильна каждой из следующих систем
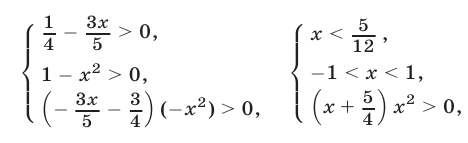
откуда следует, что 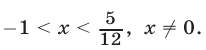
Ответ. 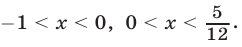
Замечание. Метод сведения неравенства (4) к равносильной ему системе (11), использованный в примере 2, часто оказывается более эффективным, чем метод замены этого неравенства на равносильную ему совокупность неравенств (5), (6) (см. пример 1).
Обращаясь к неравенству
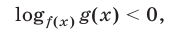
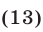
отметим, что неравенство 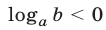 является верным при
является верным при 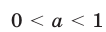 и
и 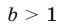 см. рис. 24.2), а также при
см. рис. 24.2), а также при 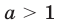 и
и 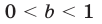 (см. рис. 24.1). Отсюда следует, что неравенство (13) равносильно совокупности двух систем неравенств
(см. рис. 24.1). Отсюда следует, что неравенство (13) равносильно совокупности двух систем неравенств
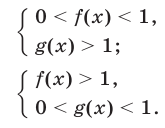
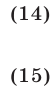
Как и для неравенства (4), совокупность систем (14) и (15) можно заменить следующей системой неравенств
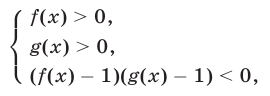
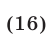
которая равносильна неравенству (13).
Пример №298.
Решить неравенство
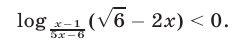
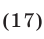
Решение:
Для неравенства (17) равносильная ему система (16) имеет вид
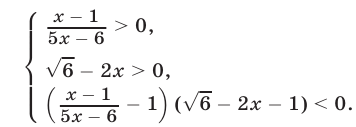
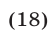
Система (18) равносильна следующей
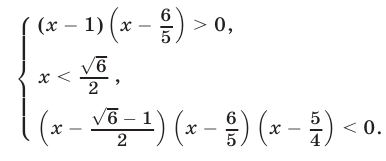
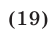
Так как 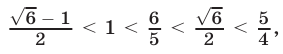 то множество решении системы (19) состоит из двух промежутков:
то множество решении системы (19) состоит из двух промежутков: 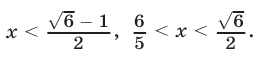
Ответ.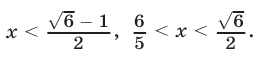
Рассмотрим неравенство
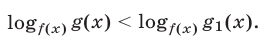
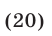
Это неравенство равносильно неравенству
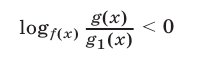
при условии, что 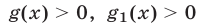 (если
(если 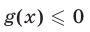 или
или 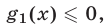 то неравенство (20) теряет смысл).
то неравенство (20) теряет смысл).
Для получения системы неравенств, равносильной неравенству (20), нужно в системе (16) добавить условие 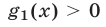 и заменить
и заменить 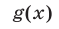 на
на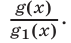
В результате имеем систему неравенств
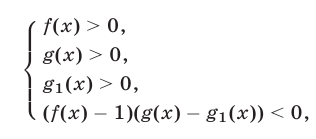
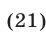
равносильную неравенству (20).
Замечание. Нестрогое неравенство
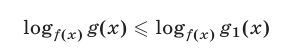
равносильно системе неравенств, которая получается из системы (21) заменой последнего ее неравенства на неравенство
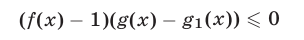
с добавлением условия 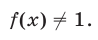
Пример №299.
Решить неравенство
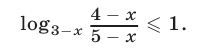
Решение:
Неравенство (22) равносильно неравенству:
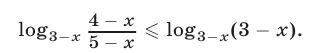
Для этого неравенства равносильная ему система неравенств (21), с учетом замечания 2, имеет вид
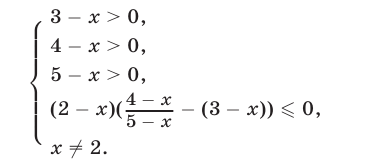
Эта система равносильна системе я: < 3,
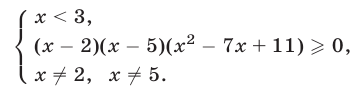
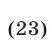
Так как уравнение 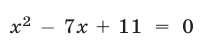 имеет корни
имеет корни 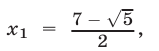
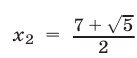 и выполняются неравенства
и выполняются неравенства 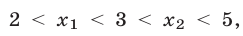 то множество решений системы (23) — совокупность двух промежутков
то множество решений системы (23) — совокупность двух промежутков 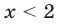 и
и 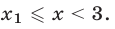
Ответ.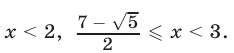
Пример №300.
Решить неравенство
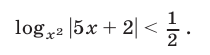
Решение:
Данное неравенство равносильно неравенству
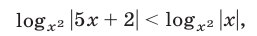
которое равносильно совокупности следующих двух систем неравенств :
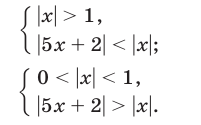
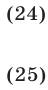
Чтобы решить системы неравенств (24) и (25), построим графики функций 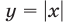 и
и 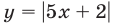 (рис. 24.7).
(рис. 24.7).
Эти графики пересекаются в точках 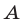 и
и  , абсциссы
, абсциссы  и
и 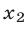 которых являются корнями соответственно уравнений
которых являются корнями соответственно уравнений 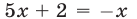 и
и 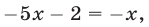 откуда находим
откуда находим 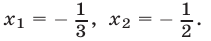
1) Если 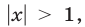 то график функции
то график функции 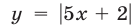 лежит выше графика функции
лежит выше графика функции 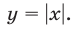 Поэтому система (24) не имеет решений.
Поэтому система (24) не имеет решений.
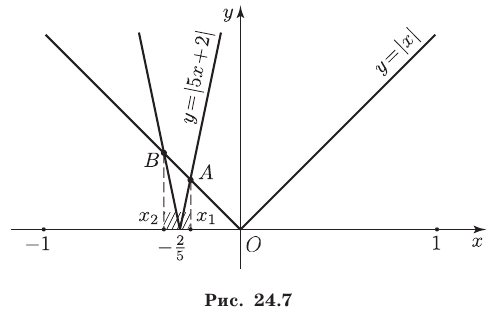
2) Если 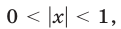 то график функции
то график функции 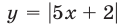 лежит выше графика функции
лежит выше графика функции 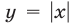 на интервалах
на интервалах 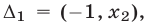
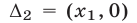 и
и 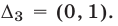 Поэтому множество решений системы (25) — объединение интервалов
Поэтому множество решений системы (25) — объединение интервалов 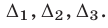
Ответ. 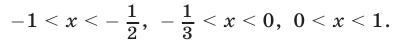
Пример №301.
Решить неравенство
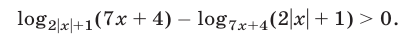
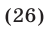
Решение:
Полагая 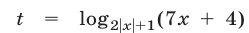 и используя формулу
и используя формулу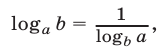 запишем неравенство (26) в виде
запишем неравенство (26) в виде
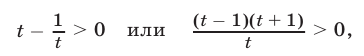
откуда следует, что либо 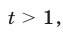 либо
либо 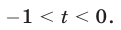
1) Пусть 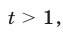 т. е.
т. е.
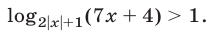
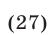
При 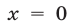 неравенства (26) и (27) теряют смысл, а при
неравенства (26) и (27) теряют смысл, а при 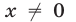 неравенство (27) равносильно неравенству
неравенство (27) равносильно неравенству
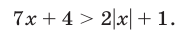
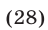
Если 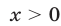 , то неравенство (28) принимает вид
, то неравенство (28) принимает вид 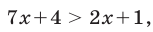 откуда следует, что
откуда следует, что 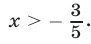 Таким образом, все положительные значения
Таким образом, все положительные значения 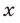 являются решениями неравенства (28) и исходного неравенства (26).
являются решениями неравенства (28) и исходного неравенства (26).
Если 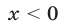 , то из (28) получаем
, то из (28) получаем 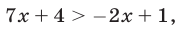 откуда
откуда 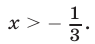
Значит, решениями неравенства (28), а также неравенства (26) являются все значения 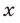 из интервала
из интервала 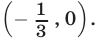
2) Пусть 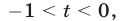 т. е.
т. е.
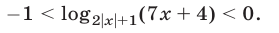
Неравенство (29) равносильно неравенству
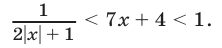
Если 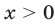 , то неравенство (30) примет вид
, то неравенство (30) примет вид
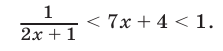
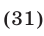
Неравенство (31) не имеет решений, так как 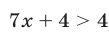 при
при 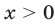 . Если
. Если 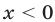 , то неравенство (30) записывается в виде
, то неравенство (30) записывается в виде
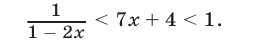
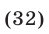
Неравенство 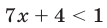 равносильно неравенству
равносильно неравенству
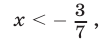
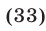
а неравенство 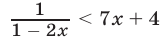 равносильно каждому из неравенств
равносильно каждому из неравенств
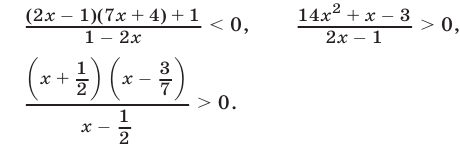
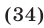
Решив неравенство (34) при условии (33), получим 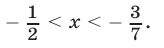
Ответ. 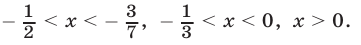
Пример №302.
Решить неравенство
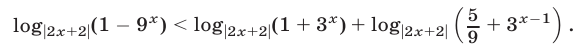
Решение:
Неравенство (35) равносильно неравенству
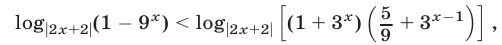
а неравенство (36) равносильно совокупности следующих систем:
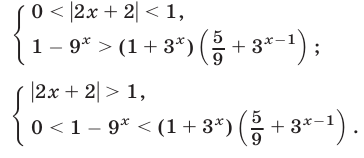

1) Рассмотрим систему (37). Первое неравенство этой системы можно записать в виде 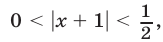 множество решений этого неравенства — интервал
множество решений этого неравенства — интервал 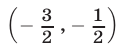 с выброшенной из него точкой
с выброшенной из него точкой 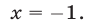
Так как 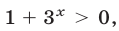 то второе неравенство системы (37) равносильно каждому из неравенств
то второе неравенство системы (37) равносильно каждому из неравенств
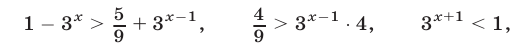
откуда 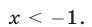 Следовательно, множество решений системы (37) интервал
Следовательно, множество решений системы (37) интервал 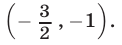
2) Обратимся к системе (38). Первое неравенство этой системы равносильно неравенству 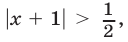 которому удовлетворяют все точки, лежащие вне отрезка
которому удовлетворяют все точки, лежащие вне отрезка 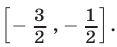
Второе неравенство системы (38) равносильно системе
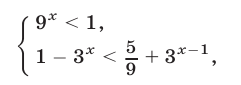
откуда следует, что 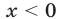 и
и 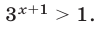
Значит, второму неравенству системы (38) удовлетворяют значения 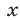 из интервала
из интервала 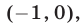 а системе (38) — точки из интервала
а системе (38) — точки из интервала 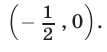
Ответ. 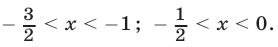
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
