Оглавление:


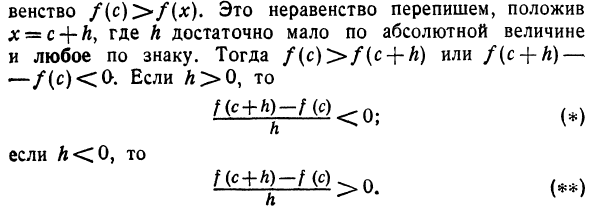




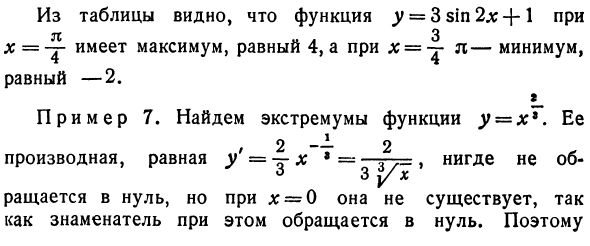


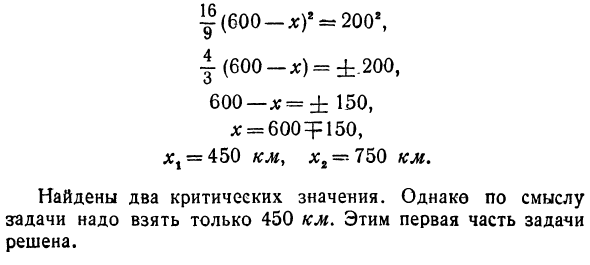



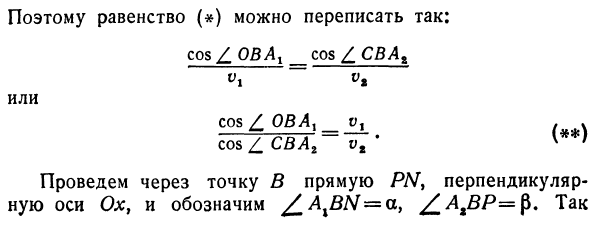
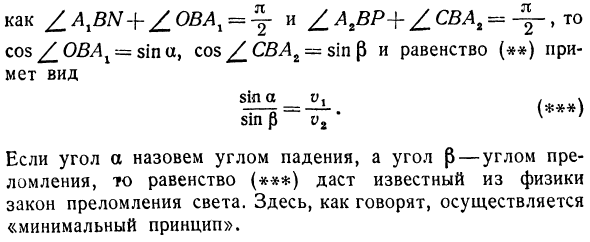

Максимальные и минимальные значения функции
- Максимальные и минимальные значения функции Значение функции f (c) называется максимальным или максимальным, если оно больше всех значений функции f (x) элемента a и немного отличается от значения c. Другими словами, мы можем найти отрезок, содержащий c как внутреннюю точку, и для x>, взятого в этом отрезке (η; / (*) Значение функции j (c) меньше всех значений функции f (x) от x, которая достаточно отличается от c, который называется минимальным или минимальным значением.
То есть найдите отрезок, который содержит c в качестве внутренней точки, и xy (x = f = c), взятый этим отрезком, имеет место неравенство f (c) sin x для всех x>, поэтому максимум Единственное важное значение — ноль. Узнайте, меняет ли производная знак при прохождении через ноль. Если π <0, производная имеет знак минус. Если x> 0, производная имеет знак плюс, поэтому производная меняет знак, когда она проходит через ноль.
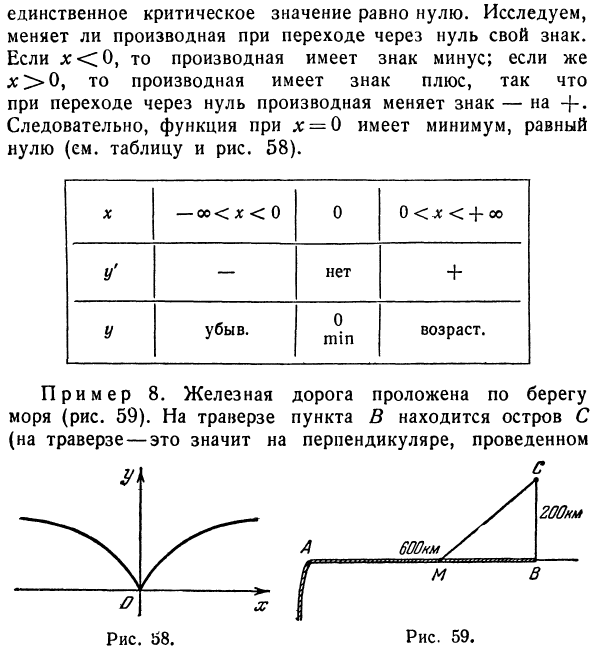
(см. Таблицу и рисунок 58). Х-оо <Х <0 0 0 <-х <+ оо Y ‘-No + В порядке убывания Возраст 0 минут. Пример 8. Железная дорога была проложена вдоль побережья (Рисунок 59). Точка Т траверса на острове С (на траверсе-это вертикально Точка B до береговой линии). Остров C поставляется из города L, который находится в 600 км от точки B по железной дороге. Расстояние до н.э. = 200 км. Груз из А на остров может быть отправлен напрямую морем или затем морем, сначала по железной дороге, а затем по морю.
Следовательно, минимальное значение для функции q: = 0 равно нулю Людмила Фирмаль
Скорость перевозки по железной дороге составляет 50 км / ч, а по морю — 30 км / ч. Стоимость перевозки груза на километр по железной дороге вдвое превышает стоимость морского транспорта. Необходимо определить положение пункта перевалки М от железной дороги до моря.
Это произошло в кратчайшие сроки от А до острова С. Кроме того, вы должны определить местоположение другого пункта перегрузки. Это обеспечивает самый дешевый транспорт. Операции загрузки не рассматриваются. Расстояние AM обозначено х. Далее из MB = 600-ху и прямоугольного треугольника MVS, AfC = =] / (600 — lg) 1 + 200a. Время, необходимое для железнодорожного транспорта / ш = -. Время потрачено на , , 1 ^ (600- *) 2 -f- 2002 ^ В океане это представляет ФМ. Это равно -1 — ^ — я-. Следовательно, время, необходимое для всей перевозки от А до С, составляет л: U (600-х) 2 + 2002 GF ~ G * M-So «G 30 В зависимости от положения x точки перегрузки M должно быть определено минимальное значение этой функции.
- Найти производную. , _- (600- *) = 3 / (600-х) 2 + 2002-5 (600-х)
50 + ЗОУ (600-х) 2 + 2002150У (600-л 🙂 2+ 2002 Уравнивание производной до нуля дает 3 Y (W — x) ‘+ 200 * -5 (600 — x) = 0. Решение этого уравнения дает: 3 | / (600 л) * + 2002 = 5 (600 л :), (600 х) г + 2002 = | (600 с) \ ^ (600-lg) 2 = 200% | (600 с) = ± .200, 600-x = ± 150, x = 600 = p 150, jct = 450 км, L: 2 = -750 км Были найдены два важных значения. Однако, по смыслу задачи, нужно пройти всего 450 км. Это решило первую часть проблемы.
Во второй части никаких дополнительных расчетов не требуется. Фактически, путь переменного тока короче, чем сломанный путь AMC, и проходит через море. Поэтому это самый дешевый путь. Поэтому самый дешевый транспорт реализуется, когда перевалочный пункт сделан в городе Л. В заключение рассмотрим вопросы, имеющие значительное физическое значение. Для однородных сред (воздух, вода, стекло и т. Д.) Это легко Здесь проблема.
Кроме того, точка M движется равномерно со скоростью v, и путь s, где точка M движется в течение определенного периода, равен s = vt. Людмила Фирмаль
Задание 1. Два разных похожих носителя соприкасаются по прямой линии (рис. 60). Точка М каждого носителя может двигаться линейно и равномерно. Для первого носителя скорость viy — вторая, а для скорости v2 точка Ax находится на первом носителе, а точка Ag — вторая. Нам нужно в кратчайшие сроки перенести точку M из Ax в Ar и определить тип пунктирной линии, по которой точка M должна двигаться.
Решения. Выберите ось координат так, чтобы ось Ox совпадала с прямой линией, которая является границей носителя, и проведите ось Oy через точку Ax, перпендикулярную оси Ox. В этой абсциссе точка Ax равна нулю, а ордината равна определенному числу yv, поэтому это Ax (0, yh). Координаты точки Ar в той же системе координат обозначены как xy yy, так что это A2 (xy y2).
Предположим, что точка / H, выходящая из Av, достигает точки B (xy 0) на границе среды. Тогда путь sv, пройденный первой средой, можно найти как расстояние между точками Ar и Wu, т.е. s <Vx2 + y . Путь st от точки B до Ar, по которому перемещалась вторая среда, выражается следующим образом. ст = Α = K (jct — x) гг. Время движения в первой среде Vx * + y \ TX ~ —.
Время движения второго носителя t2 =: V (xt-x) * + y \ -. В результате г То же от А до Ав , , + A, V (xt-x) ‘+ yl 1 «г VX + X xt— * » Время t изменяется путем изменения положения точки B (x, 0) на оси Oxy. Поэтому в задаче необходимо определить минимальное значение функции t. Для этого найдите его производную: х. — Х Vl Vx * + y \ vt Y (xl-x) w + y1 ‘Если производная равна нулю, = 0, v.Vx ‘+ yl vtV {x% -x? + у \ Откуда д: -х «» Uhg + v2V (xt-xy + yl ‘ но = JTri = cos Z.0BAV Vwtf ^ = cos cos CBA. V (xt-xr + £ BA «^ 1
Поэтому знак равенства (#) можно переписать следующим образом: cos ^ OBAL _ cos или потому что, _. cos £ swag ~~ ‘e’ Проведите линию / W через точку 5, перпендикулярную оси Ox, обозначив £ AXBN = a.Z.AxBN + Z.OBAx = \ and /.AtBP+/_CBAt=^-y и т. Д. zos / _OWA ^ -smUy cos CZM2 = sin | 3 и уравнение (**) принимает вид грешить () грех р v 2 Если угол a называется углом падения, а угол (угол 5 преломления), уравнение () дает закон преломления света, известный в физике.
Я разница между -y и менее 2n, в этом случае «Достаточно маленький» означает меньше, чем второй. Конечно, функция sin x имеет несколько максимальных значений. Пример 3. Докажем, что функция / (x) = x2-4x-5 имеет минимальное значение x-2. По этой причине / (2) <; ) Или / () — / (2)> 0 фактически, f (x) — / (2) = ish * ‘- *** до {x2-4x — 5) — (2 * —4 -2-5) = -x2-4n: -5 + 9 = jc2—4jc + 4 = (x-2) 2> 0. Здесь мы смогли доказать, что неравенство / (2) <; / () справедливо для всех значений x} и не только достаточно близко к числу 2. , 56). В общем, трудно доказать существование, а также найти экстремальные ценности.
Следующая теорема помогает решить эту проблему. Теорема 1 (условия, необходимые для существования экстремальных значений). Если крайнее значение функции f (x) находится при x = c, то производная при x = c равна нулю или не существует вообще. Доказательство этой теоремы выполняется только в максимальном случае (в минимальном случае доказательство повторяется и меняется только знак неравенства).
Поэтому убедитесь, что функция / () имеет максимум при x = c. То есть, если все х достаточно близко к с, Равно / (s)> / (*). Перепишите это неравенство, установив x = c + d. Здесь Λ имеет достаточно малое абсолютное значение и имеет все знаки. Тогда f (c)> f (c + h) или f (c + h) — / (c) <0. Если Λ> 0, nc + h) -HO 0. (f) L Если A <0, f (c + h) -f (c)> 0 ^
Функция f (x) для x = c: 1) нет производной, 2) есть производная. Случай 1) доказывает теорему. Если имеет место случай 2), из-за определения производной / (C) = H ^ W ^ W () Предотвращает производную / ‘(c) от положительного числа. Отрицательный или равен нулю. Кроме того, благодаря (*) производная не может быть отрицательной и может быть положительной или нулевой. При поиске производной h должен быть как положительным, так и отрицательным, поэтому производная должна быть равна нулю, чтобы избежать несоответствий. Теорема доказана.
Доказанная теорема дает необходимые условия существования экстремальных значений. Это означает, что если существует экстремум, возможно, будет выполнено одно из указанных условий. Однако одно из этих условий может быть выполнено, и крайнее значение может не существовать. Вот пример. Пример 4. Рассмотрим функцию / (x) = (x — 2) 8 + 1. Его производная / = 3 (x — 2) 2 исчезает с * = 2. / (2) = (2-2) 24 -1 = 1, где x <2 f (x) меньше 1 и x> 2 равно 2 или больше. Таким образом, невозможно указать сегмент, который содержит x = 2 внутри и всегда имеет / (2)> / (jt) или / (2) </ (*), то есть / (2) не Здесь нет крайней ценности.
Таким образом, эти значения можно найти по доказанной теореме Хотя это независимая переменная, которая может быть экстремальным значением, невозможно утверждать существование экстремального значения на основе этой теоремы. Чтобы найти экстремальное значение, используйте теорему, которая обеспечивает достаточные условия существования экстремального значения. Заранее согласен использовать определенные выражения.
Если функция задана в сегменте, содержащем x = c, если x <.c и функция имеет отрицательное значение, а x> c и значение положительное, то « функция добавляет знак минус при передаче x = c (И если x = c, функция может не существовать).После этого разъяснения значение фразы «После прохождения x = c функция меняет знак плюс на знак минус» также становится понятным. При использовании этих выражений обратите внимание на существование функции при x = s. Теорема 2 (достаточное условие существования экстремальных значений).
Если функция f (x) определена и является непрерывной в интервале, включающем x = c, и производная f ′ (x 🙂 этой функции проходит через x ~ c, изменяя знак плюс на минус, тогда x = c Функция развернута, изменение знака минус на плюс, когда производная проходит xc, минимизирует функцию с x = c. Рассмотрим случай, когда знак меняется с положительного на отрицательный. По условию производная положительна для всех значений x, меньших c. Это означает, что функция увеличивается. То есть, если x c, то f (c)> f (x). Таким образом, интервал всегда имеет / (c) >> ((*), что также означает, что / (c) является максимальным значением функции. Также рассматривается переход со знака минус на знак плюс.
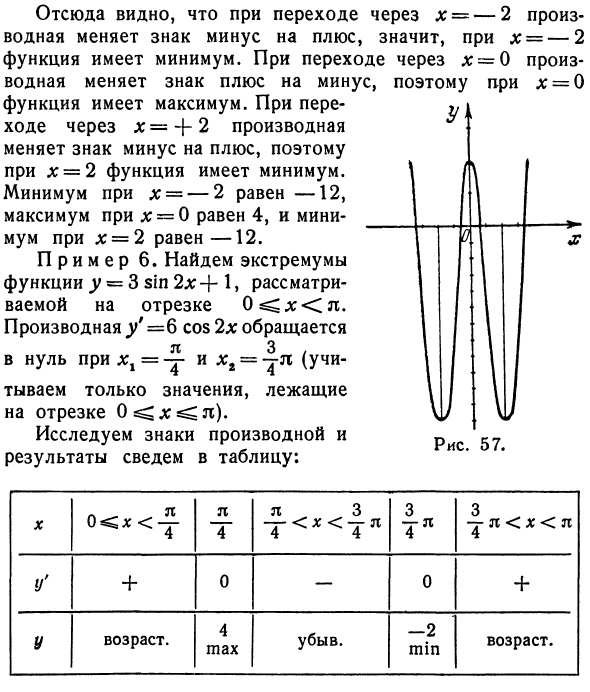
Пример 5. Найти предельное значение функции y = x4-8d: * + 4. Его производная равна y ‘= 4x * -16 *. Это, как известно, непрерывно. Поэтому найдите критическое значение, сделав производную равной нулю и решив полученное уравнение. 4x * -16x = 0; 4x (x * -4) = 0; xx = -2; x = 0; x $ = 2.В результате были получены три важных значения (рисунок 57). Изучите признаки производной, как показано ранее, и суммируйте результаты в таблице. X -co <* <-2 -2 -2 Y ‘-0 + 0-0 + В порядке убывания Возраст -12 минут. 4 чек -12 минут.
Это указывает на то, что производная меняет знак минус на положительный при прохождении x = -2. То есть, если x = -2, функция имеет минимальное значение. После прохождения je = 0 производная меняет знак плюс на минус. Следовательно, если l: = 0, функция максимальна. После прохождения jc == + 2, производная меняет знак минус на положительный. Следовательно, если x = 2, функция минимальна. Минимальное значение при x = -2 равно -12, максимальное значение при x = 0 равно 4, а минимальное значение при x = 2 равно -12.
Пример 6. Найти экстремальное значение функции y = 3 sin 2x + 1, рассматриваемой в отрезке O ^ <q; <π. Производная y ‘= 6 cos 2x инвертировать л 3, -А = ноль для -l (учитывать только значения в сегменте 0 ^ x C n) 57 с производными знаками Результаты сведены в таблицу. X 4 l T l 3- <x <-t l 4 4 3 7ya 3 -7- L <X <l 4 Y ‘+ 0-0 + Есть возраст. 4 чека — возраст 2 минуты.
Из таблицы видно, что максимальное значение x = function y = 3 sin 2x + 1 равно 4, а минимальное значение * = равно –2. г Пример 7. Найти экстремальное значение функции y-xr. она 2 -2. 2 Производная, равная V = -x 1 = o, нигде д 3 Дж / х Он исчезает, но не существует, когда x = 0, потому что знаменатель исчезает. так
Смотрите также:
| Возрастание и убывание функции | Выпуклость и вогнутость линии. Точка перегиба |
| Исследование функций на возрастание и убывание | Общий план исследования функций и построения графиков |
