Оглавление:
Сущность метода интегрирования по частям вполне соответствует его названию. Дело в том, что при вычислении интеграла этим методом подынтегральное выражение 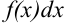 представляют в виде произведения двух множителей
представляют в виде произведения двух множителей 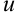 и
и 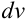 , причем
, причем 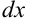 обязательно входит в
обязательно входит в 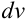 . Далее пользуются формулой интегрирования по частям:
. Далее пользуются формулой интегрирования по частям:
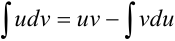
При вычислении интегралов методом по частям главным является разумное разбиение подынтегрального выражения на 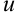 и
и 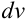 . Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям:
. Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям:
- Если под знаком интеграла встречается логарифмическая или обратные тригонометрические функции
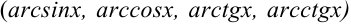 , то их обозначают за
, то их обозначают за 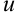 , остальные множители — за
, остальные множители — за 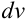 .
. - В интегралах вида
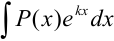 ,
, 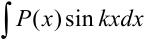 ,
, 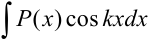 , где
, где 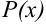 — многочлен,
— многочлен, 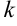 —
— 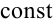 , за
, за 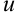 принимают многочлен
принимают многочлен 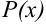 , остальные множители — за
, остальные множители — за 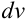 .
.
Для нахождения неопределенного интеграла методом по частям можно использовать следующий алгоритм:
- Разбиваем подынтегральное выражение на
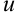 и
и 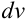 (в соответствии с правилом, рассмотренным выше).
(в соответствии с правилом, рассмотренным выше). - Находим
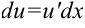 и
и 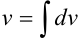 .
. - Подставляем
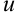 ,
, 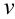 ,
, 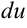 и
и 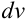 в формулу
в формулу 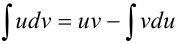 и вычисляем получившийся интеграл.
и вычисляем получившийся интеграл.
Рассмотрим применение метода интегрирования по частям на примерах.
Пример №19.10.
Найдите 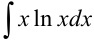 .
.
Решение:
1. Поскольку под знаком интеграла встречается логарифмическая функция, то ее принимаем за 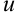 :
: 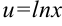 . Остальные множители принимаем за
. Остальные множители принимаем за 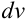 :
: 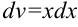 .
.
2. Находим 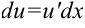 :
: 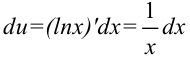 .
.
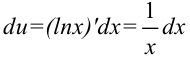
Находим 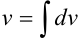 :
: 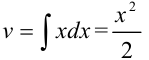 (полагаем
(полагаем 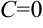 ).
).
3. Воспользуемся формулой 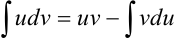 :
:
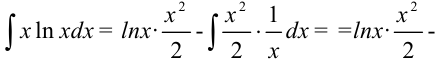
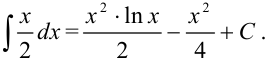
Ответ: 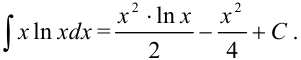
Пример №19.11.
Найдите 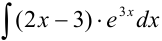 .
.
Решение:
1. Исходный интеграл имеет вид 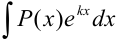 , следовательно, за
, следовательно, за 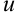 принимают многочлен
принимают многочлен 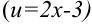 , остальные множители — за
, остальные множители — за 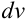 :
: 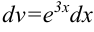 .
.
2. Находим 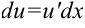 :
: 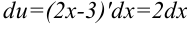 .
.
Находим 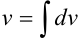 :
: 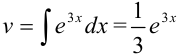 (полагаем
(полагаем 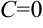 ).
).
3. По формуле 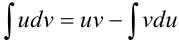 имеем:
имеем:
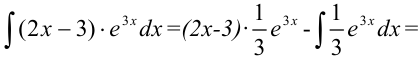
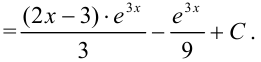
Ответ: 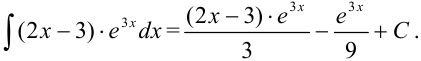
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Интегралы от некоторых сложных функций. |
| Интегрирование методом замены переменной (методом подстановки). |
| Интегрирование простейших рациональных дробей. |
| Интегрирование некоторых иррациональных функций. |
