Оглавление:
Метод оценок
При решении задач в целых числах иногда используется подход, основанный на построении и применении различного рода оценок выражений, входящих в условия задач. Рассмотрим примеры.
Пример №55.
Доказать, что уравнение
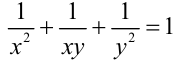
не имеет целых положительных решений.
Доказательство. Пусть, ради определённости, 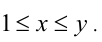 Тогда
Тогда
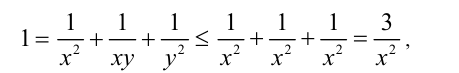
откуда находим оценку 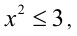 т.е.
т.е. 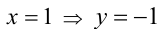 — не удовлетворяет условию задачи. Аналогично рассматривается случай
— не удовлетворяет условию задачи. Аналогично рассматривается случай 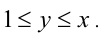
Пример №56.
Сумма обратных величин трёх натуральных чисел равна 1. Найти эти числа (наборы, а не упорядоченные тройки).
Решение:
Пусть x,y,z — искомые натуральные числа. Условия задачи приводят к уравнению
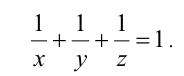
Очевидно, что для того чтобы это равенство выполнялось, необходимо, чтобы хотя бы одно из чисел не превосходило 3. Без ограничения общности будем считать, что 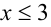 . Тогда X = 2 или X = 3 .
. Тогда X = 2 или X = 3 .
1) Пусть X = 2 , тогда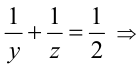 хотя бы одно из чисел у или z не превосходит 4. Ради определённости, пусть это
хотя бы одно из чисел у или z не превосходит 4. Ради определённости, пусть это 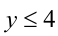 . Тогда у = 3 или у = 4 . В первом случае z = 6 , и имеем три числа
. Тогда у = 3 или у = 4 . В первом случае z = 6 , и имеем три числа 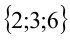 . Во втором случае Z = 4 , и находим ещё одну тройку {2;4;4}.
. Во втором случае Z = 4 , и находим ещё одну тройку {2;4;4}.
2) Пусть теперь X = 3, тогда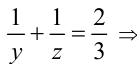 хотя бы одно из чисел у или z не превосходит 3. Ради определённости, пусть это
хотя бы одно из чисел у или z не превосходит 3. Ради определённости, пусть это 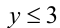 . Тогда у = 2 или у = 3. В первом случае z = 6 , и имеем числа {3;2;6} — уже было. Во втором случае z = 3 , и получаем набор { 3;3;3} .
. Тогда у = 2 или у = 3. В первом случае z = 6 , и имеем числа {3;2;6} — уже было. Во втором случае z = 3 , и получаем набор { 3;3;3} .
Ответ: это наборы чисел {2;3;6}, {2;4;4}, {3;3;3}.
Пример №57.
Найти все упорядоченные тройки (x,y,z) натуральных чисел, удовлетворяющих равенству
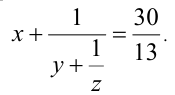
Решение:
Приведём уравнение к виду 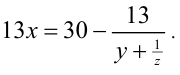
Так как 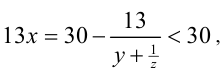 , то получаем:
, то получаем: 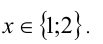
1) Если x = 1, то, подставляя в уравнение, находим 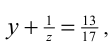 , что невозможно, так левая часть в этом равенстве больше 1, а правая — меньше 1.
, что невозможно, так левая часть в этом равенстве больше 1, а правая — меньше 1.
2) Если x = 2 , то получаем 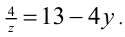 Справа стоит целое число, следовательно,
Справа стоит целое число, следовательно, 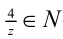 , откуда
, откуда 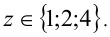 При z = 1 имеем
При z = 1 имеем 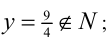 при z = 2 имеем
при z = 2 имеем 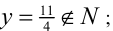 при z = 4 находим у = 3 . Ответ:
при z = 4 находим у = 3 . Ответ: 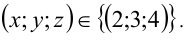
Пример №58.
Непустое множество X состоит из конечного числа N натуральных чисел. Чётных чисел в X меньше двух третей от N , а нечётных не больше 36% от N . Какое минимальное значение может принимать число N ?
Решение:
Пусть n — число нечётных чисел в X . По условию,
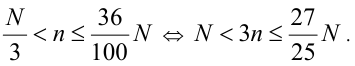
Воспользуемся тем свойством, что для целых чисел m,k строгое неравенство 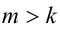 равносильно нестрогому
равносильно нестрогому 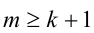 . Поэтому
. Поэтому
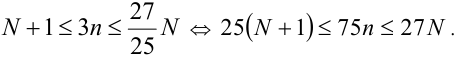
По свойству транзитивности из последнего неравенства получаем, как следствие, оценку
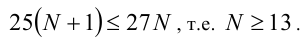
Далее действуем перебором (с проверкой).
Если N = 13 , то, подставив в неравенство (1), получим: 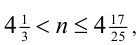 что невозможно при целых n .
что невозможно при целых n .
Если N = 14, то, подставив в неравенство (1), получим: 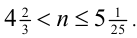 Этому условию удовлетворяет n= 5 (т.е. нашлось n). Ответ:
Этому условию удовлетворяет n= 5 (т.е. нашлось n). Ответ: 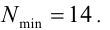
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
