Оглавление:
Метод возведения в степень
Метод возведения в степень является одним из наиболее распространённых методов решения задач с иррациональностями. Как уже отмечалось выше, при его использовании следует помнить, что любое уравнение и неравенство всегда можно возвести в нечётную степень, это преобразование является равносильным. Другое дело, если уравнение необходимо возвести в чётную степень. В общем случае это переход к следствию, чреватый появлением посторонних корней. Это допустимо, если возможно сделать проверку корней. Если же проверка по какой-либо причине затруднена или невозможна (например, когда при решении неравенств и некоторых уравнений получается бесконечно много решений), то следует сохранять равносильность выполняемых преобразований. Для этого перед очередным возведением в чётную степень следует не забывать выписывать условие неотрицательности обеих частей уравнения.
Если уравнение содержит несколько радикалов, то для последовательного избавления от них уравнение приходится возводить в степень несколько раз. В этом случае перед очередным возведением в степень часто используют приём уединения корня.
Пример №220.
Решить уравнение
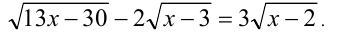
Решение:
ОДЗ :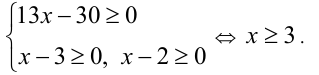 
Далее метод возведения в степень (в данном случае в квадрат, так как в уравнение входят квадратные корни) можно применить двумя способами.
1-й способ. Приведём уравнение к виду
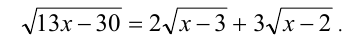
Обе части уравнения неотрицательны, поэтому, возведя его в квадрат, получим равносильное (на ОДЗ) уравнение:
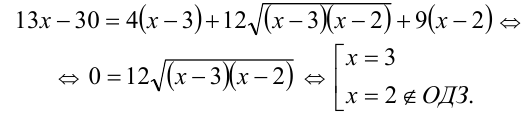
2-й способ. Сразу возведём уравнение в квадрат
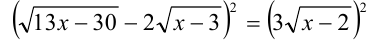
(переход к следствию) и, упростив, запишем в виде
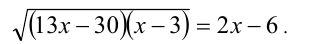
Разложим полученное уравнение на множители
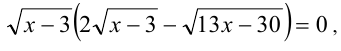
и сведём к совокупности
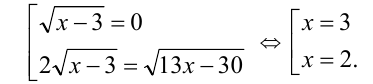
Так как в процессе решения задачи был переход к следствию, то необходимо сделать проверку полученных значений x подстановкой в ОДЗ или исходное уравнение (или в любое уравнение, равносильное исходному). Число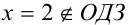 
(посторонний корень, образовавшийся из-за возведения в квадрат без учёта совпадения знаков обеих частей уравнения). Получаем тот же ответ. Ответ: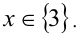 
Пример №221.
Решить уравнение
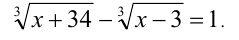
Решение:
1-й способ. Возведём неравенство в куб, используя формулу
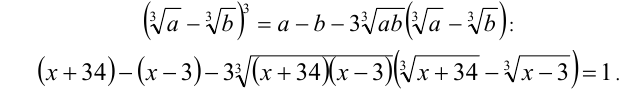
Заменяя, в силу исходного уравнения, выражение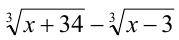 
единицей и упрощая, получаем, как следствие, уравнение
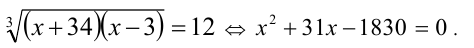
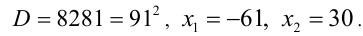Проверка показывает, что оба значения удовлетворяют исходному уравнению.
2-й способ. Приведём уравнение к виду
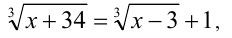
и после этого возведём его в куб:
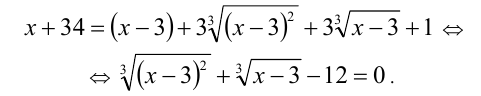
Решая это уравнение как квадратное относительно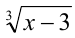 
, находим:
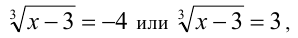
откуда получаем те же значения x .
Следует отметить, что второй способ в данном случае предпочтительней, так как полученное в конце квадратное уравнение имеет более простые коэффициенты (и не надо делать проверку). Ответ: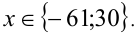 
Пример №222.
Решить уравнение
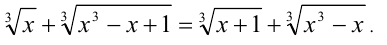
Решение:
Возведём обе части уравнения в куб (равносильное преобразование):
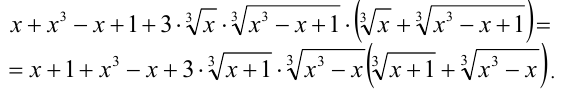
Заменяя выражение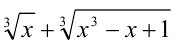 
выражением 
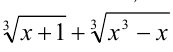, получим уравнение, являющееся следствием исходного:
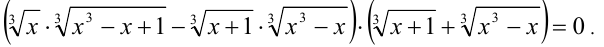
Это уравнение сводится к совокупности двух уравнений:
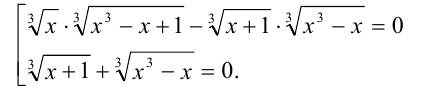
Решения первого уравнения есть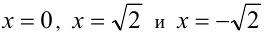 
. Второе уравнение имеет одно решение 
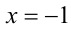. Проверка показывает, что все четыре значения являются корнями исходного уравнения. Ответ: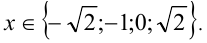 
Пример №223.
Решить неравенство
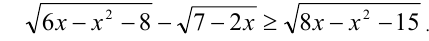
Решение:
Выпишем ОДЗ: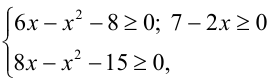 
но не будем сразу решать эту систему. Приступим к решению неравенства, переписав его в виде
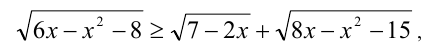
добившись того, чтобы обе части неравенства стали неотрицательны (иначе неравенство возводить в квадрат нельзя). Только после этого возведём в квадрат, перейдя к равносильному (на ОДЗ) неравенству
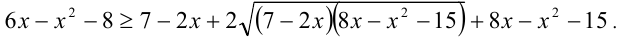
После упрощения получим
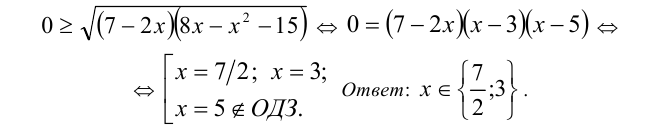
Пример №224.
Решить уравнение
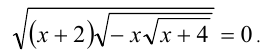
Решение:
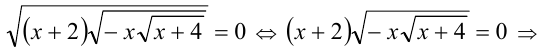
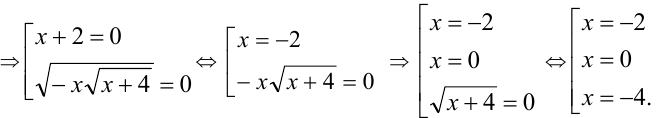
Проверка подстановкой в исходное уравнение показывает, что все три числа являются решениями уравнения.
Замечание. Иногда при решении этой задачи записывают ОДЗ так:
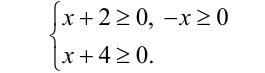
Хочется предостеречь читателя от таких попыток, поскольку первые два условия в системе неверны, что подтверждается наличием среди корней уравнения числа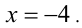 
На самом деле ОДЗ выглядит следующим образом:
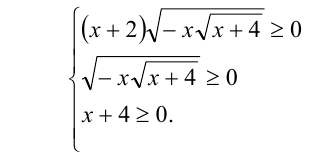
Пример №225.
Решить уравнение
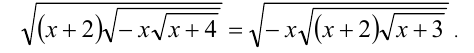
Решение:
Заметим, что x = -2 и x = 0 являются решениями уравнения (а числа x = — 4 и x = -3 — не являются). Найдём корни этого уравнения, отличные от x = -2 и x = 0 . Для них, согласно ОДЗ,
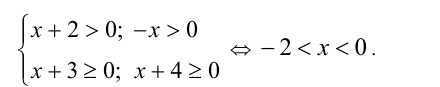
Возведём уравнение в квадрат, получив равносильное (на ОДЗ) уравнение:
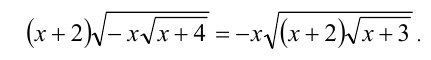
Обе части последнего равенства положительны при — 2 < x < 0 , поэтому, возводя его в квадрат ещё раз, придём к равносильному равенству
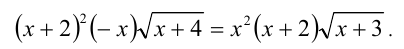
Сократив на x+ 2(> 0) и х(< 0), получим уравнение
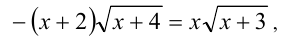
обе части которого отрицательны при -2 < x < 0 . Поэтому, возводя ещё раз в квадрат, получим уравнение, равносильное предыдущему:
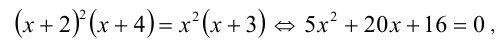
корни которого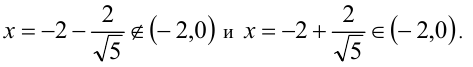 
Ответ: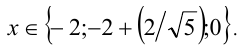 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
