Оглавление:
Метод замены переменных
Пример №51.
Доказать, что произведение четырёх последовательных целых чисел в сумме с 1 даёт полный квадрат.
Решение:
По условию, требуется доказать, что выражение
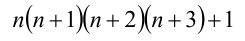
является квадратом целого числа. Сгруппируем сомножители следующим образом: 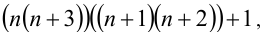 и положим
и положим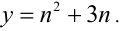 Тогда
Тогда
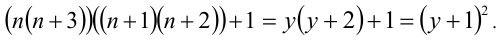
Выполняя обратную подстановку, приходим к ответу.
Ответ: 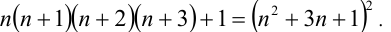
Рассмотрим, далее, пример, в котором последовательно используются сразу несколько приёмов: замена переменной, одна из формул сокращённого умножения (см. п. 1.3.) и анализ остатков.
Пример №52.
Доказать, что для любого натурального 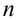 ,
, 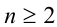 , число
, число 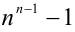 делится нацело на
делится нацело на 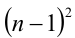
Доказательство. Обозначим 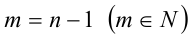 Требуется доказать, что для любого натурального
Требуется доказать, что для любого натурального 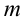 число
число 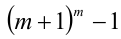 делится нацело на
делится нацело на 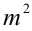 . Воспользуемся формулой сокращённого умножения
. Воспользуемся формулой сокращённого умножения
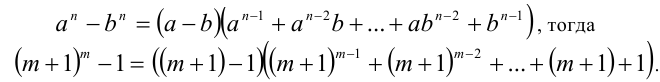
Первый из двух сомножителей делится на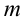 . Покажем, что и второй сомножитель кратен
. Покажем, что и второй сомножитель кратен 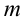 . Действительно, во вторых скобках стоит сумма
. Действительно, во вторых скобках стоит сумма 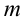 чисел, делящихся на
чисел, делящихся на 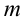 с остатком 1. При сложении таких чисел остатки складываются, поэтому их сумма будет делиться на
с остатком 1. При сложении таких чисел остатки складываются, поэтому их сумма будет делиться на 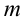 с остатком
с остатком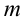 , т.е. с остатком 0. Утверждение доказано.
, т.е. с остатком 0. Утверждение доказано.
В уравнениях, решаемых в целых числах, также иногда целесообразна замена переменных.
Пример №53.
Найти все целочисленные решения уравнения 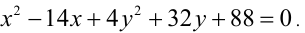
Решение:
Выделяя полные квадраты, приведём уравнение к виду
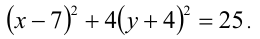
Положим 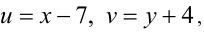 тогда имеем:
тогда имеем: 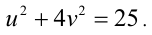
Отсюда получаем оценки: 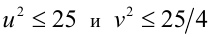 (с учётом целочисленности
(с учётом целочисленности 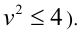 Заметим, что в силу симметричности наряду с парами (u;v) решениями уравнения (*) будут пары (u;—v), (— u;v) и (—u;—v). Поэтому найдём вначале лишь неотрицательные целые значения u и v :
Заметим, что в силу симметричности наряду с парами (u;v) решениями уравнения (*) будут пары (u;—v), (— u;v) и (—u;—v). Поэтому найдём вначале лишь неотрицательные целые значения u и v :
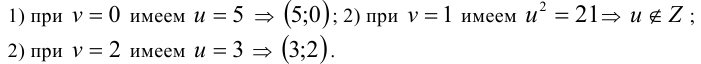
Итак, решения уравнения (*):
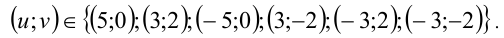
Возвращаясь к первоначальным переменным, получим ответ.
Ответ: 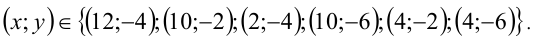
Пример №54.
Решить в натуральных числах уравнение
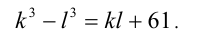
Решение:
Поскольку правая часть равенства 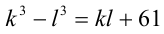 положительна, то
положительна, то 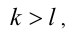 а значит, можно представить
а значит, можно представить 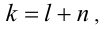 где
где 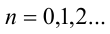 Такая подстановка позволяет свести уравнение третьей степени относительно обеих переменных к более простому квадратному уравнению относительно l. Действительно, подставляя выражение l+n в исходное уравнение, получим квадратное уравнение
Такая подстановка позволяет свести уравнение третьей степени относительно обеих переменных к более простому квадратному уравнению относительно l. Действительно, подставляя выражение l+n в исходное уравнение, получим квадратное уравнение 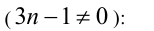
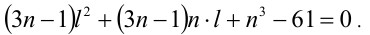
Для того чтобы это уравнение имело решения, необходимо и достаточно неотрицательности его дискриминанта:
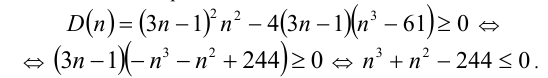
Для решения последнего неравенства рассмотрим функцию 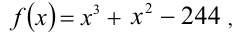 , её график — кубическая парабола. Имеем:
, её график — кубическая парабола. Имеем: 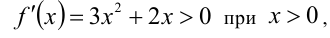 следовательно, функция возрастает при натуральных значениях аргумента. Так как
следовательно, функция возрастает при натуральных значениях аргумента. Так как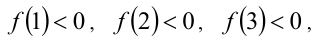
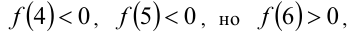 то решениями неравенства
то решениями неравенства 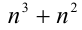
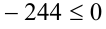 будут
будут 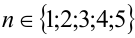 . Проверка показывает, что только при n = 1 дискриминант
. Проверка показывает, что только при n = 1 дискриминант 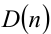 является полным квадратом:
является полным квадратом: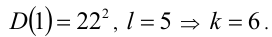
Ответ. 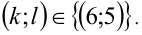
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
