Чтобы решить линейные дифференциальные уравнения первого порядка применяют метод Бернулли. Основа метода заключается в том, что используется подстановка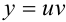 
, где 
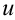и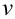 
— некоторые функции от переменной 
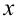. Тогда для нахождения 
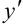можно применить правило дифференцирования произведения: 
.
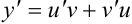Рассмотрим сущность метода Бернулли на конкретном примере.
Пример №40.1.
Найдите общее решение дифференциального уравнения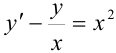 
.
Решение:
Данное уравнение — линейное дифференциальное уравнение первого порядка.
1. Выполним подстановк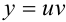и: и :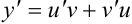
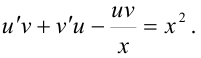
2.Сгруппируем члены, содержащие 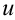, и вынесем 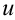за скобки:
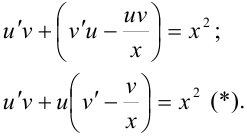
3. Считая, что неизвестная функция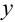 
является произведением двух также неизвестных функци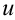й и 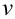, мы можем одну из этих функций (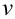) выбрать произвольно. Поэтому приравняем к нулю выражение, стоящее в скобках, и найдем функцию :
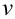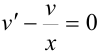— уравнение с разделяющимися переменными, для решения которого представим
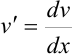. Тогда:
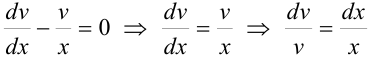. Взяв интегралы от обеих частей, получим, что
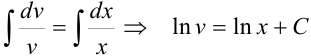. Но поскольку функцию 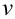мы выбираем произвольно, удобно константу 
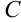взять равной нулю. Тогда 
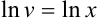, a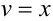 
.
Таким образом, на третьем шаге мы нашли функцию ().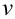
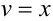4. Вернёмся к уравнению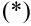 
. Поскольку выражение в скобках на третьем шаге мы выбирали равным нулю, то данное уравнение 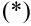примет вид: 
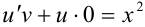или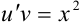 
.
Подставим функцию 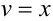в это уравнение и найдем вторую функцию :
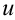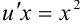. Данное уравнение легко приводится к простейшему делением обеих частей на :
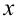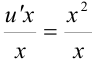или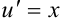 
. Тогда 
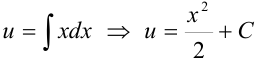. Константу 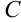здесь писать обязательно!
Итак, на четвертом шаге метода Бернулли мы нашли функцию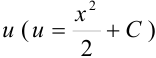 
.
5. Решением исходного уравнения будет являться функция 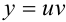. Функци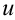и и 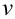были найдены нами на 3-м и 4-м этапе решения примера. Подставив их в уравнение 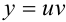, найдем, что
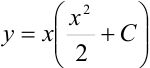— общее решение дифференциального уравнения .
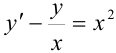Ответ: .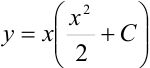
Из приведенного примера несложно установить алгоритм решения линейных дифференциальных уравнений первого порядка:
- Привести дифференциальное уравнение к виду
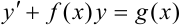и ввести подстановк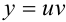и: и 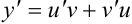. - Сгруппировать члены, содержащие 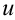, и вынести 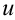за скобки.
- Приравнять к нулю выражение, стоящее в скобках, и найти функцию 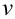(необходимо решить дифференциальное уравнение с разделяющимися переменным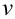и и 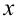). Функция 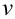не должна содержать константу !
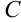- Вернуться к дифференциальному уравнению, полученному после шага 2. Подставить в это уравнение функцию 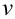, найти вторую функцию 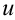(функция 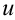содержит константу ).
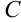- Подставить функци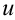и и 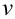, найденные на 3-м и 4-м этапе, в уравнение 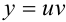. Полученная функция 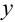является общим решением исходного линейного дифференциального уравнения.
Замечание. На 3-м шаге решения линейного дифференциального уравнения требуется выразить функцию 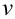через 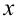. Во избежание возможных трудностей, рассмотрим некоторые конкретные примеры, показывающие, как из полученного уравнения выразить :
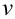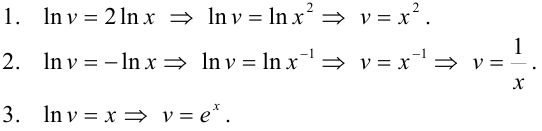
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
