Оглавление:
Задача 3.27.
Методом Франка- Вулфа найти решение задачи 3.22, состоящей в определении максимального значения функции
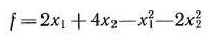
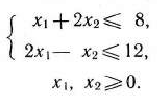
Решение:
Найдем градиент функции
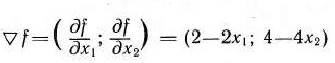
и в качестве исходного допустимого решения задачи возьмем точку 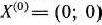 , а в качестве критерия оценки качества получаемого решения — неравенство
, а в качестве критерия оценки качества получаемого решения — неравенство 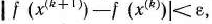 , где
, где 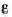 = — 0.01
= — 0.01
I итерация. В точке 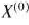 градиент
градиент 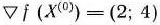 . Находим максимум функции
. Находим максимум функции
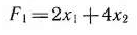
при условиях (63) и (64)
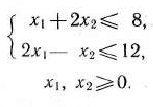
Задача (65) —(67) имеет оптимальный план 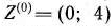 . Найдем новое допустимое решение исходной задачи по формуле (61):
. Найдем новое допустимое решение исходной задачи по формуле (61):
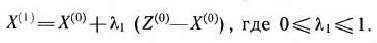
Подставив вместо 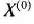 и
и 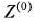 их значения, получим
их значения, получим
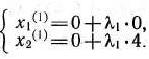
Определим теперь число 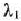 . Подставив в равенство (62) вместо
. Подставив в равенство (62) вместо 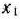 и
и 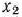 их значения в соответствии с соотношениями (69)
их значения в соответствии с соотношениями (69)
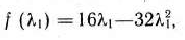
найдем производную этой функции по 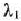 и приравняем ее нулю:
и приравняем ее нулю:
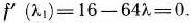
Решая это уравнение, получим 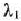 =1/4 = 0,25. Поскольку найденное значение заключено между 0 и 1, принимаем его за величину шага. Таким образом,
=1/4 = 0,25. Поскольку найденное значение заключено между 0 и 1, принимаем его за величину шага. Таким образом,
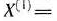
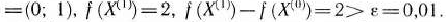
II итерация. Градиент целевой функции исходной задачи в точке 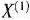 есть
есть 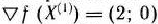 . Находим максимум функции
. Находим максимум функции
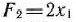
при условиях (63) и (64). Решением является 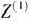 = (6, 4; 0, 8).
= (6, 4; 0, 8).
Определяем теперь
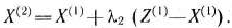
Последнее равенство перепишем следующим образом:
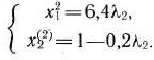
Подставляя теперь в функцию (62) вместо 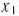 и
и 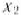 их значения в соответствии с соотношениями (70), получаем
их значения в соответствии с соотношениями (70), получаем
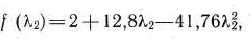
откуда
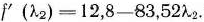
Приравнивая 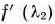 нулю и решая полученное уравнение, находим
нулю и решая полученное уравнение, находим 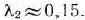 . Таким образом,
. Таким образом,
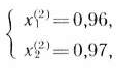
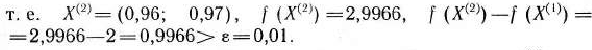
III итерация. Градиент функции 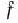 в точке
в точке 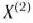 есть
есть
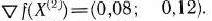
Находим максимум функции 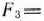
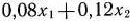 при условиях (63) и (64). Решением является
при условиях (63) и (64). Решением является
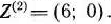
Определяем
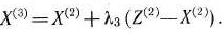
Имеем
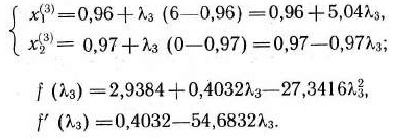
Решая уравнение
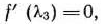
находим
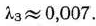
Следовательно,
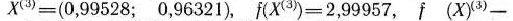
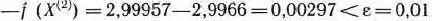
Таким образом,
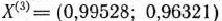
является искомым решением исходной задачи. Данная точка находится достаточно близко к точке максимального значения целевой функции 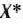 =(1; 1), найденной при решении этой задачи в § 3.3. Задав меньшую величину
=(1; 1), найденной при решении этой задачи в § 3.3. Задав меньшую величину 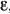 , можно было, совершив дополнительные приближения, еще ближе подойти к точке максимального значения целевой функции.
, можно было, совершив дополнительные приближения, еще ближе подойти к точке максимального значения целевой функции.
Метод штрафных функций. Рассмотрим задачу определения максимального значения вогнутой функции
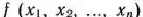
при условиях
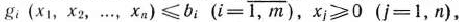
где
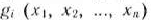
выпуклые функции.
Вместо того чтобы непосредственно решать эту задачу, находят максимальное значение функции

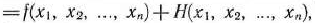
являющейся суммой целевой
функции задачи, и некоторой функции
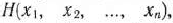
определяемой системой ограничений и называемой штрафной функцией. Штрафную функцию можно построить различными способами. Однако наиболее часто она имеет вид

где
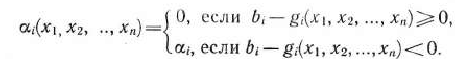
а 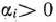 — некоторые постоянные числа, представляющие собой весовые коэффициенты.
— некоторые постоянные числа, представляющие собой весовые коэффициенты.
Используя штрафную функцию, последовательно переходят от одной точки к другой до тех пор, пока не получат приемлемое решение. При этом координаты последующей точки находят по формуле
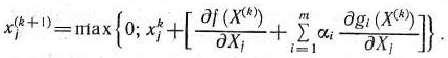
Из последнего соотношения следует, что если предыдущая точка находится в области допустимых решений исходной задачи, то второе слагаемое в квадратных скобках равно нулю и переход к последующей точке определяется только градиентом целевой функции. Если же указанная точка не принадлежит области допустимых решений, то за счет данного слагаемого на последующих итерациях достигается возвращение в область допустимых решений. При этом чем меньше а,, тем быстрее находится приемлемое решение, однако точность определения его снижается. Поэтому итерационный процесс обычно начинают при сравнительно малых значениях а, и, продолжая его, эти значения постепенно увеличивают.
Итак, процесс нахождения решения задачи выпуклого программирования методом штрафных функций включает следующие этапы:
- Определяют исходное допустимое решение.
- Выбирают шаг вычислений.
- Находят по всем переменным частные производные от целевой функции и функций, определяющих область допустимых решений задачи,
- По формуле (72) находят координаты точки, определяющей возможное новое решение задачи.
- Проверяют, удовлетворяют ли координаты найденной точки системе ограничений задачи. Если нет, то переходят к следующему этапу. Если координаты найденной точки определяют допустимое решение задачи, то исследуют необходимость перехода к последующему допустимому решению И случае такой необходимости переходит к этапу 2, в противном случае найдено приемлемое решение исходной задачи.
- Устанавливают значения весовых коэффициентов и переходят к этапу 4.
Задача 3.28.
Найти максимальное значение функции
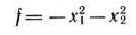
при условиях
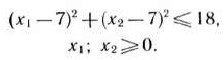
Решение:
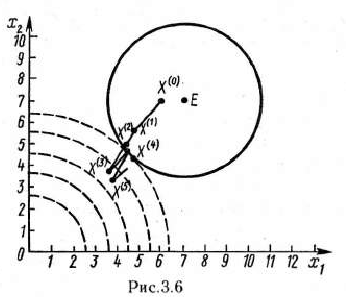
Целевая функция данной задачи представляет собой отрицательно-определенную квадратичную форму и, значит, вогнута. В то же время область допустимых решений задачи, определяемая ограничениями (74) и (75), — выпуклая. Следовательно, задача (73) — (75) является задачей выпуклого программирования. Для нахождения ее решения применим метод штрафных функций. Прежде чем это сделать, построим область допустимых решений задачи (рис. 3.6) и линии уровня, определяемые целевой функцией (73). Этими линиями служат окружности с центром в точке (0; 0). Точка касания одной из этих окружностей с областью допустимых решений и является искомой точкой максимального значения целевой функции.
Положим
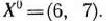
Возьмем
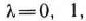
обозначим через
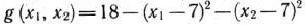
и определим частные производные от функций 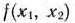 и
и 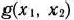 по переменным
по переменным 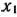 и
и 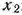 :
:
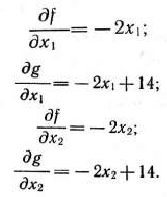
Теперь, используя формулу (72), приступаем к построению последовательности точек, одна из которых определит приемлемое решение.
I итерация. Так как точка 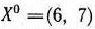 принадлежит области допустимых решений задачи, то второе слагаемое в квадратных скобках формулы (72) равно нулю. Значит, координаты следующей точки
принадлежит области допустимых решений задачи, то второе слагаемое в квадратных скобках формулы (72) равно нулю. Значит, координаты следующей точки  вычисляем по формулам
вычисляем по формулам
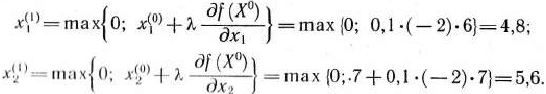
Проверим теперь, принадлежит ли эта точка области допустимых решений задачи. Для этого найдем
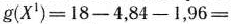
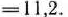
Так как
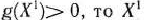
принадлежит области допустимых решений. В этой точке
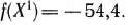
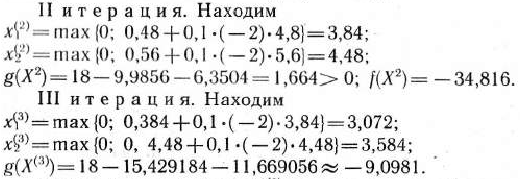
IV итерация. Точка не принадлежит области допустимых решении задачи. Следовательно,
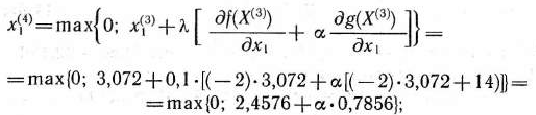
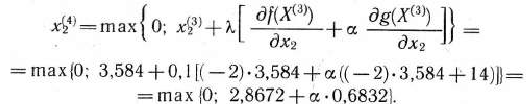
Здесь возникает вопрос о выборе числа 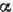 . Наиболее целесообразно взять его так, чтобы точка
. Наиболее целесообразно взять его так, чтобы точка 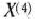 не слишком далеко удалялась от границы области допустимых решений и вместе с тем принадлежала этой области. Этим требованиям удовлетворяет, в частности,
не слишком далеко удалялась от границы области допустимых решений и вместе с тем принадлежала этой области. Этим требованиям удовлетворяет, в частности, 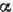 = 1,9. При данном значении получаем
= 1,9. При данном значении получаем

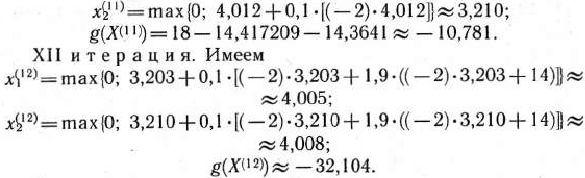
Сравнивая значения целевой функции, найденные в точках, полученных после X и XII итераций, видим, что они с точностью до 10″‘ совпадают. Это говорит о близости точки, найденной на последней итерации, к точке максимального значения целевой функции. Такой же вывод можно сделать, если исследовать векторы-градиенты функций 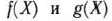 в точке
в точке 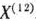 . В этой точке
. В этой точке
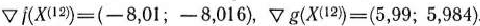
Вычислим отношения одноименных координат векторов: —8,01/ 5,99а —1,337; —8,016/5,984»—1,339. Как видно, они почти равны между собой. Это означает, что векторы 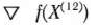 и
и 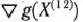 практически коллинеарны. Так как к тому же точка
практически коллинеарны. Так как к тому же точка 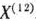 находится вблизи границы области допустимых решений (поскольку
находится вблизи границы области допустимых решений (поскольку
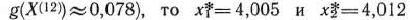
можно считать приемлемым решением задачи. Это решение при необходимости можно уточнить дальнейшими шагами до полной коллинеарности градиентов целевой и ограничительной функций.
Последовательность точек, получаемых во время нахождения решения задачи, наглядно иллюстрируется рис. 3.6.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
