Мгновенный центр ускорений

Мгновенный центр ускорений

Мгновенным центром ускорений называется точка твердого тела, ускорение которой в данный момент времени равно нулю. Для определения такой точки рассмотрим ускорения точек твердого тела в плоскопараллельном движении. Обозначая через 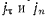проекции ускорения произвольной точки твердого тела на касательную и нормаль к траектории этой точки, будем иметь

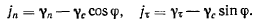
Подставляя в эти соотношения значения 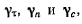получим

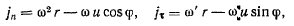
где 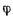— угол между радиус-вектором точки М, построенным из
мгновенного центра вращения, и направлением ускорения точки С
(рис. 78). Введя обозначение 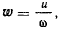представим предыдущие формулы в виде

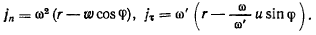
Если R — радиус кривизны рулетты точки М, то нормальное ускорение можно будет представить в виде

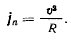
Это выражение обращается в нуль при 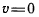или при 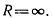В
последнем случае точка М является точкой перегибов. Если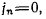
то из уравнений (а) получим при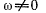

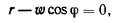
или

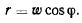
Величина 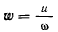является одной и той же для всех точек твердого тела. Геометрическое место точек, удовлетворяющих
уравнению (b), есть окружность радиуса 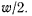Рулетты на этой
окружности имеют точки перегибов, поэтому полученную окружность называют

кругом перегибов, или кругом Лагира. Нормальные ускорения точек твердого тела, совпадающих с кругом Латра, равны нулю, а касательные ускорения проходят через точку К окружности, которую назовем полюсом перегибов. Замечание. В случае поступательного движения твердого тела 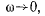и радиус круга Лагира стремится к бесконечности.

Рассмотрим теперь геометрическое место точек твердого тела,
для которых обращается в нуль тангенциальное ускорение 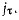Пусть
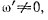тогда из формул (а) получим

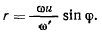
Геометрическое место точек, удовлетворяющее этому уравнению,
является окружностью радиуса 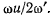Если 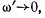то радиус этой
окружности неограниченно возрастает. Не будем рассматривать
случай, когда 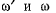и со одновременно обращаются в нуль (случай
поступательного движения), и будем предполагать, что эти величины отличны от нуля и конечны. На окружности обращаются в нуль касательные ускорения, и, следовательно, имеет место условие

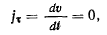
т. е. скорость принимает стационарное значение. Поэтому полученную окружность называют кругом стационарности (или кругом Бресса). Ускорения всех точек твердого тела, совпадающих с кругом Бресса, направлены к мгновенному центру вращения твердого тела. В точке S, пересечения кругов Бресса и Лагира, обращаются в нуль и касательное и нормальное ускорения. Поэтому ускорение точки S твердого тела равно нулю. Точка S является мгновенным центром ускорений твердого тела.

Круг стационарности и круг перегибов пересекаются в двух
точках S и С. Но точка С является мгновенным центром
вращения, а потому в ней будет равно нулю нормальное ускорение.
Ускорение же 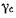точки С параллельно скорости точки С в момент 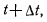т. е. направлено по касательной к траектории точки С и
отлично от нуля. Определяя предельное значение ускорения при
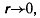заметим, что поскольку 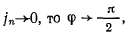и тогда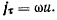
Если связать подвижную систему координат с твердым телом,
то из теоремы Кориолиса будем иметь 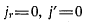и ускорения
точек твердого тела будут определяться формулой Ривальса

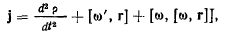
где 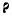— радиус-вектор начала подвижной системы координат. Если
за начало подвижной системы координат выбрать точку твердого
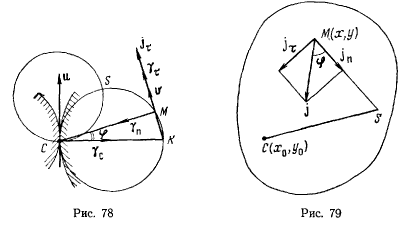
тела, совпадающую с мгновенным центром ускорений, то 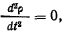и ускорения точек твердого тела будут распределяться так, как будто твердое тело вращается вокруг неподвижной оси, ортогональной к плоскости движения твердого тела и проходящей через мгновенный центр ускорений (рис. 79). Формулы, определяющие мгновенный центр ускорений и ускорения произвольной точки твердого тела в плоскопараллельном движении, можно получить и непосредственно из формул Эйлера. Обозначая через 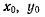координаты мгновенного центра вращения
твердого тела в неподвижной системе координат, а через х, у —
координаты произвольной точки твердого тела, для проекций
скоростей точек твердого тела получим равенства

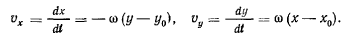
Отсюда для проекций ускорений точек твердого тела на неподвижные оси координат будем иметь следующие соотношения:

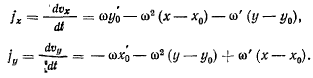
Обозначая через 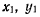координаты той точки твердого тела, ускорение которой равно нулю, для определения этих координат получим равенства

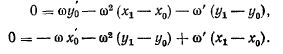
Система линейных неоднородных алгебраических относительно разностей 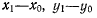уравнений имеет решение, если определитель системы отличен от нуля

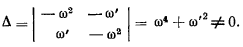
Система линейных неоднородных алгебраических относительно
разностей 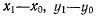уравнений имеет решение, если определитель
системы отличен от нуля

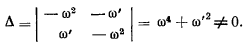
Это условие выполняется, когда хотя бы одна из величин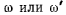
отлична от нуля, что всегда имеет место, если движение твердого
тела не является поступательным. В этом случае координаты
точки твердого тела, ускорение которой равно нулю (мгновенного
центра ускорений) определяются из равенств

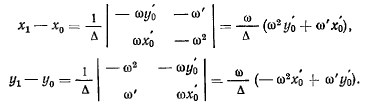
Вычитая уравнения 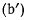из соответствующих уравнений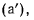
получим уравнения для определения ускорений точек твердого тела

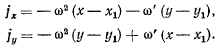
Эти формулы допускают простое геометрическое истолкование: ускорения точек твердого тела распределяются так, как будто твердое тело вращается вокруг мгновенного центра ускорений, и могут быть представлены касательной и нормальной составляющими

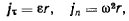
где 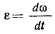угловое ускорение твердого тела.

Если обозначить через <р угол между направлением ускорения и
прямой, соединяющей точку М с мгновенным центром ускорений, то

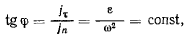
т. е. этот угол является общим для всех точек твердого тела. Величина же ускорения

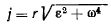
пропорциональна расстоянию точки до мгновенного центра ускорений.

Пример:

Стержень АВ вращается с постоянной угловой скоростью
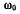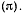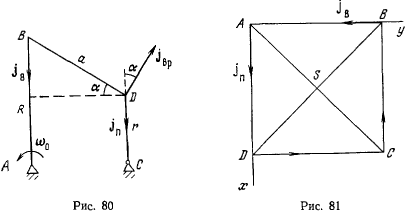
вокруг своего неподвижного конца в неподвижной плоскости В этой же плоскости 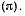вокруг точки С может вращаться стержень DC. Концы В и D стержней соединены шарнирно с третьим стержнем ВО. Определить ускорение точки D в тот момент, когда стержни АВ и DC параллельны между собой и ортогональны к отрезку АС. Длина стержня DC равна r, длина отрезка BD равна а (рис. 80)

Решение:

В рассматриваемом положении мгновенный центр вращения стержня BD уходит в бесконечность, а его угловая скорость вращения равна нулю, т. е. стержень BD совершает мгновенно-поступательное движение. Скорости точек В и D равны по величине и по направлению

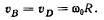
Точка D совершает движение но окружности радиуса r, и ее центростремительное ускорение

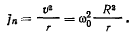
Вычислим ускорение точки D по формуле Ривальса, принимая за полюс точку В стержня BD:

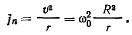
Здесь ускорение точки В будет только центростремительным при вращении вокруг точки А

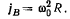
Осестремительное ускорение точки D равно пулю, поскольку равна нулю мгновенная угловая скорость вращения стержня BD. Вращательное же ускорение точки

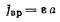
содержит неизвестную величину 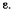Определяя центростремительную составляющую ускорения точки D из формулы (а), получим

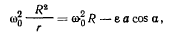
где

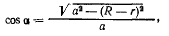
откуда

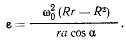
Тогда вращательная составляющая ускорения точки D

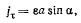
и полное ускорение точки D получит вид

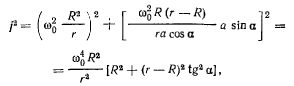
где

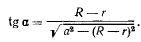
Пример:

Квадрат ABCD со стороной а совершает движение в плоскости чертежа. Найти положение мгновенного центра ускорений и ускорение вершин его С и D если известны в данный момент ускорения точек А и В (рис.81).

Решение:

Определим сначала мгновенную угловую скорость и угловое ускорение квадрата, воспользовавшись формулой Ривальса:

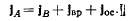
Проектируя это равенство на оси х и у, получим

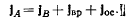
откуда

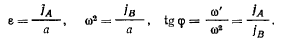
Если величины 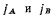равны, то мгновенный центр ускорений находится в центре квадрата, а ускорения точек D и С направлены по сторонам квадрата и по величине равны ускорениям точек А к В.

Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Теорема Ривальса

Распределение ускорений

Кинематические уравнения эйлера

Замечание о конечных перемещениях твердого тела