Оглавление:
Наибольший общий делитель, наименьшее общее кратное, алгоритмы их нахождения и свойства
Сформулируем несколько определений, имеющих отношение к понятиям наибольшего общего делителя и наименьшего общего кратного.
Если каждое из натуральных чисел 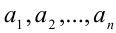 делится нацело на натуральное число b , то говорят, что число b является их общим делителем. Так, числа 12 и 18 имеют общие делители 1, 2, 3, 6.
делится нацело на натуральное число b , то говорят, что число b является их общим делителем. Так, числа 12 и 18 имеют общие делители 1, 2, 3, 6.
Если два или несколько натуральных чисел не имеют общих натуральных делителей, отличных от единицы, то эти числа называются взаимно простыми. При этом каждое из них в отдельности не обязательно должно быть простым. Например, числа 7 и 9 — взаимно простые; 4, 5 и 6 — взаимно простые.
Так как числа 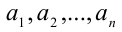 могут иметь лишь конечное число общих натуральных делителей, то среди них всегда имеется наибольший, который называется наибольшим общим делителем и обозначается НОД
могут иметь лишь конечное число общих натуральных делителей, то среди них всегда имеется наибольший, который называется наибольшим общим делителем и обозначается НОД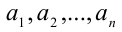 . В случае взаимно простых чисел он равен единице.
. В случае взаимно простых чисел он равен единице.
Рассмотрим стандартный алгоритм нахождения НОД (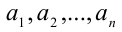 )
)
1) Разложим каждое из чисел 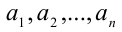 на простые множители;
на простые множители;
2) перебирая все различные простые множители, входящие хотя бы в одно из этих чисел, возьмём каждый из них в наименьшей степени, с которой он входит в числа 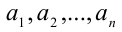 ;
;
3) перемножим взятые множители (с наименьшими степенями вхождения). Полученное число и будет НОД(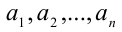 ).
).
Если натуральное число а является кратным для каждого из чисел 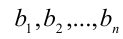 (т.е. делится на любое из этих чисел нацело), то а называется общим кратным чисел
(т.е. делится на любое из этих чисел нацело), то а называется общим кратным чисел 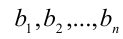 . В частности, произведение нескольких натуральных чисел всегда является их общим кратным. Среди всех общих кратных данных чисел
. В частности, произведение нескольких натуральных чисел всегда является их общим кратным. Среди всех общих кратных данных чисел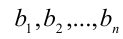 (их бесконечно много) всегда имеется наименьшее; оно называется наименьшим общим кратным и обозначается
(их бесконечно много) всегда имеется наименьшее; оно называется наименьшим общим кратным и обозначается
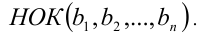
Стандартный алгоритм нахождения наименьшего общего кратного нескольких чисел состоит в следующем:
- разложим все числа на простые множители;
- в отличие от алгоритма нахождения наибольшего общего делителя, возьмём каждый из простых множителей в наибольшей из степеней, с которыми он входит в разложение чисел
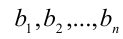 ;
; - перемножим эти множители (с наибольшими степенями вхождения). Полученное в результате число и будет
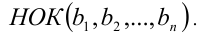
Можно определить понятия наибольшего общего делителя и наименьшего общего кратного для произвольных целых (ненулевых, но не обязательно натуральных) чисел. Так, наибольшим общим делителем целых чисел 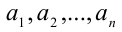 называется такой положительный общий делитель чисел
называется такой положительный общий делитель чисел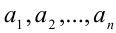 , который делится на любой другой общий делитель этих чисел. Наименьшим общим кратным отличных от нуля целых чисел
, который делится на любой другой общий делитель этих чисел. Наименьшим общим кратным отличных от нуля целых чисел 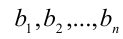 называется наименьшее положительное число, кратное всем этим числам.
называется наименьшее положительное число, кратное всем этим числам.
Как уже отмечалось, отыскание НОД двух натуральных чисел а и b требует предварительного разложения этих чисел на простые множители. Это несложно сделать, если числа невелики, но разложить на множители многозначные числа бывает трудно. Существует способ отыскания НОД, требующий лишь умения делить с остатком (см. следующий пункт). Этот способ предложил в свое время Евклид, поэтому он называется алгоритмом Евклида и основан на следующих утверждениях.
- Если
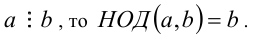
- Если при делении а на b получается ненулевой остаток q, т.е.
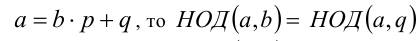 и задача сводится к более простой задаче отыскания НОД(а,q).
и задача сводится к более простой задаче отыскания НОД(а,q). - Если
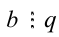 , то
, то 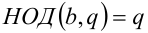 , и тогда
, и тогда 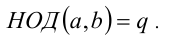
- Если при делении b на q получается ненулевой остаток
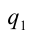 , т.е.
, т.е. 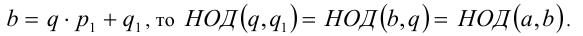
- Продолжая описанный процесс, получаем все меньшие и меньшие остатки. В конце концов, дойдём до остатка, на который будет делиться предыдущий остаток. Этот наименьший отличный от нуля остаток и будет наибольшим общим делителем чисел а и b .
Перечислим наиболее важные свойства НОД и НОК, позволяющие лучше изучить природу этих понятий.
Свойства НОД и НОК
Для любых натуральных a,b,C,d справедливы следующие свойства.
- Переместительное свойство:
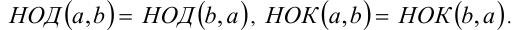
2. 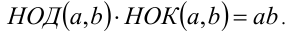 В частности, если
В частности, если 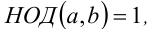 то
то 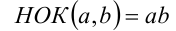 (свойство верно только для двух чисел а,b).
(свойство верно только для двух чисел а,b).
3. Если 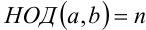 , то найдутся такие натуральные числа С, d , что
, то найдутся такие натуральные числа С, d , что 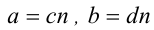 , причём
, причём 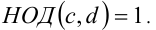
4. Если 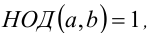 то
то 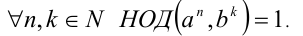
5. Если 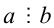 , то
, то 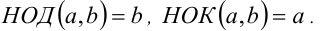
6.Общий множитель С можно выносить из-под знаков НОД и НОК:
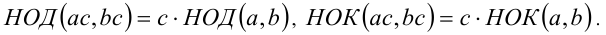
7.Два (три) последовательных натуральных числа взаимно просты:
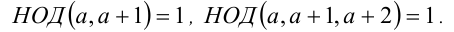
8.Пошаговое (,последовательное) вычисление НОД и НОК:
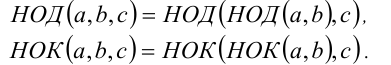
9.Если b > а , то НОД(а,Ь)= НОД(а,b- а).
10. Если при делении числа а на число b получается ненулевой остаток q 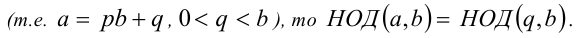
Знание указанных свойств позволяет на практике упрощать решение многих задач, в которых используются понятия НОД и НОК.
Деление с остатком
Пусть имеются два числа а и b 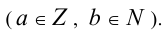 Разделить целое число а на натуральное число b с остатком значит найти два целых числа р и q таких, что справедливо равенство
Разделить целое число а на натуральное число b с остатком значит найти два целых числа р и q таких, что справедливо равенство
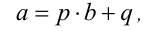
где р называется частным, a q — остатком от деления а на b , причём 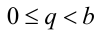 . Эта формула носит название формулы деления целого числа на натуральное с остатком, и такое представление единственно.
. Эта формула носит название формулы деления целого числа на натуральное с остатком, и такое представление единственно.
В частности, если q = 0. то целое число а делится нацело на натуральное число b . Если 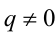 , то р называется неполным частным.
, то р называется неполным частным.
Сравнимость по модулю
Рассмотрим в связи с понятием остатков от деления ещё одно полезное определение. Если два целых числа а и b при делении на натуральное число n дают один и тот же остаток q , где 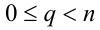 , то числа а и b называют сравнимыми по модулю n . Это обозначают следующим образом
, то числа а и b называют сравнимыми по модулю n . Это обозначают следующим образом
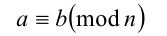
и читают: « а равно b по модулю п ».
Можно доказать, например, что введённая таким образом операция сравнения обладает следующими свойствами.
1. Два числа, сравнимые с третьим по одному и тому же модулю, сравнимы между собой (по этому же модулю):
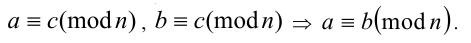
2. Сравнения по одному модулю можно складывать:
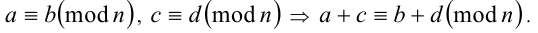
Остаток суммы нескольких чисел по модулю п равен сумме остатков слагаемых по модулю n . То есть, проще говоря, при сложении чисел их остатки (от деления на одно и то же число n) также складываются.
3.Сравнения по одному модулю можно почленно перемножать:
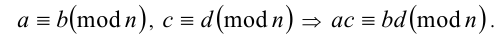
Остаток произведения нескольких чисел по модулю п равен произведению остатков сомножителей по модулю п . Т.е., проще говоря, при перемножении чисел их остатки (от деления на одно и то же число п ) также перемножаются.
4. Обе части сравнения и модуль можно умножить на одно и то же целое число:
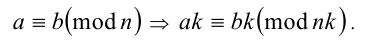
В следующей задаче эффективно используются некоторые из свойств операции сравнения по модулю.
Пример №1.
Найти остатки от деления на 8:
1) суммы 88881 + 88882 + 88883 + 88884 + 88885,
2) произведения 88881 • 88882 • 88883 • 88884 • 88885 , не выполняя непосредственно сложения и умножения.
Решение:
1) Числа 88881,88882,88883,88884,88885 при делении на 8 дают соответственно остатки 1,2,3,4,5. То есть 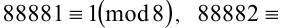
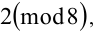
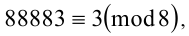
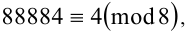
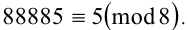
Тогда по свойству 2 имеем
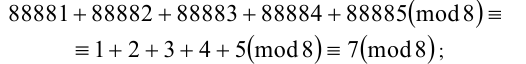
2) По свойству 3 имеем
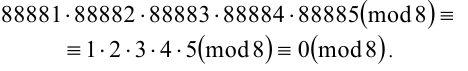
Ответ: остаток от деления суммы на 8 равен 7; остаток от деления произведения на 8 равен 0.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
