Оглавление:


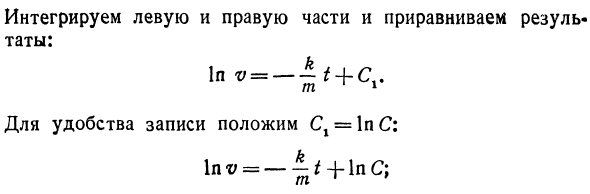





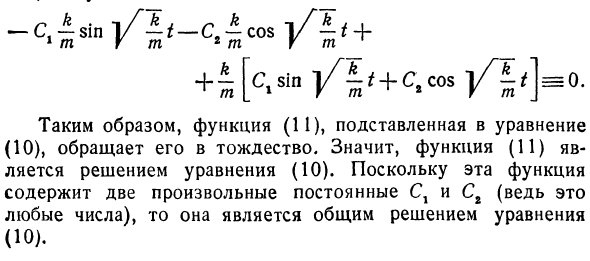


Некоторые дифференциальные уравнения, встречающиеся в механике
- Некоторые дифференциальные уравнения, встречающиеся в механике Если точка движется вдоль оси Ox под действием силы F, t представляет время, а x — расстояние от начала координат, точечная скорость v определяется первым pro. Производная v = gy, ускорение a является второй производной, т.е. a = ~. Связь между силой, точечной массой и ускорением Общие решения могут быть написаны в разных форматах. Си Син Y \ 1 ‘Ки Yl> \ — / Cf + cj т + х = соз Vc \ + c \ Vc \ + CI Поставить C, О _ -_ = cos f,. 2 = sin w, -1 f C \ + C2 = A, Vci + ci V Vc \ + c \ V > φsin / Ат + sinφcos] / «- * j, l; = Лsin ^ + тогда х = А или (12) Коэффициент А называется амплитудой и часто Его фаза ph.
Глава Вы можете видеть, что решение IV, § 1 и уравнения (10) представляет собой синусоидальную волну, то есть вибрирующее движение. Уравнение (10) называется уравнением гармонических колебаний. Рений установлен законом Ньютона. (1) F = это или (2) DV или (3) Вот пример дифференциального уравнения, полученного с использованием этого закона.
Приложенная сила равна произведению массы и ускорения. Людмила Фирмаль
Пример 1. Точка движется под действием силы против движения пропорционально скорости точки. Сначала точка находилась в начале координат, а скорость точки была v0. Найдите закон движения, то есть отношение между расстоянием от начала координат до момента и времени. d’х В этом примере величина силы F равна kvy, а сила направлена на движение, поэтому Применение закона вида (2) дает дифференциальное уравнение первого порядка. dv, t -jj — кв в Отдельные переменные. DV Интегрируйте левую и правую части и выровняйте результаты. 1n <r / = -t + Ct т 1 1 Для удобства описания используется C1 = 1pC. т 1
Чтобы укрепить, мы имеем -А, V ^ -Cet. (4) Это общее решение проблемы. Поскольку скорость составляла r> 0 в первый момент / = 0, подстановка t = 0 и v = v0 в уравнение (4) находит значение C. _ A: v0 = Ce C = v0; Таким образом, уравнение (4) принимает вид: v = vQe rn. (5) Это личное решение. Однако эта проблема не была решена, так как не было найдено зависимости от x /.
- Из-за того что дх / гч 1 / = -, выражение (5) можно переписать в следующем формате (6) Это также дифференциальное уравнение первого порядка. Отдельные переменные. dx = v0e t dt. (7) Если левая и правая стороны объединены отдельно, и результаты равны, _k х = -> е + кр. (8)
для (8) 0 = — + Отсюда = Получите частное для этого значения Cr из общего решения (8) или Это решение проблемы. Вот конкретный пример, который смягчает предыдущую проблему. Пример 2. Моторная лодка весом 245 кг движется прямо и равномерно со скоростью 10 м / с. В какой-то момент, считающийся ранним, двигатель останавливается, и лодка замедляется из-за трения с водой. Через одну секунду после остановки двигателя скорость лодки составила 8 м / с, но вам нужно найти скорость лодки и пройденное расстояние на этот раз через 5 секунд. Примечание Сила трения лодки относительно воды пропорциональна скорости и противодействует движению.
В первой точке точка находилась в начале координат, поэтому присваивая значения / = 0 и :: = 0 Людмила Фирмаль
Коэффициент пропорциональности получается из опыта. Применение предыдущего обозначения задачи дает y = 10 м \ сек. Вес лодки составляет 245 кг, поэтому ее масса равна -245 Предположим, что on- и ^ = 9,8 м \ сек = 25. Добавление этих данных в уравнение (5) v = \ 0e 25. (5 ‘) Эта формула еще не подходит для расчетов, потому что k неизвестно. Но через одну секунду мы еще не использовали тот факт, что скорость лодки составляет 8 м / с. Подставляя эти данные из наблюдений в уравнение (5 ‘), мы можем найти k.
Давайте сделаем это: k_ 8-10 Откуда Логарифмически с обеих сторон этого выражения вы найдете –25 ^ = 0, 8, whice 0,8 при k = -25 Следовательно, коэффициент пропорциональности k найден. Тогда уравнение (5 ‘) принимает следующий вид: x = 10 ?? πn — »= 10 (* log0’8) <= 10 (0,8) ‘.
Отсюда, желаемая скорость может быть определена путем замены t-b секунд. v = 10 (0,8) 5 = 10 3,3 м / с. Подстановка найденного значения k и данных значений m, v0 и t = -5 в уравнение (9) найдет путь, пройденный за 5 секунд. х == —10 м- Пример 3. Рассмотрим движение точки под действием силы F = -kx. Возьмите закон Ньютона в виде (3), тогда d2x, dzx, k л / 1ЛЧ = -Yy; или -r ^^ — x = 0. (10) d * 2 ‘dtz 1 t v’ Это дифференциальное уравнение второго порядка. Формула x = Cl sin] / ^ + C2cos t (11) Его общее решение. Для этого мы находим £ = Cl l / Icos l / ^ -C, cff 1 U m U m 2 U t U t C.- sin j / — / — С-cos l / d / 2 1 мг т 1 т U т
Подстановка второй производной и самой функции в уравнение дает:-Ct-sin V —t-C2-cos V + 1 м 2 м 2 + Mc> sin Vlt + c> C0S Таким образом, функция (11), назначенная уравнению (10), преобразует его в тождество. Следовательно, функция (I) является решением уравнения (10). Поскольку эта функция содержит две произвольные постоянные C и C2 (которые в конце концов являются произвольными числами), она является общим решением уравнения (10).
Смотрите также:
| Основные определения | Движение точки на плоскости. Система дифференциальных уравнений |
| Дифференциальные уравнения первого порядка | Определители (основные понятия) |
