Оглавление:
Необходимые и достаточные условия экстремума
Рассмотрим условия существования экстремума функции.
Теорема 46.1 (необходимые условия экстремума). Если в точке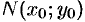 
дифференцируемая функция 
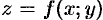имеет экстремум, то ее частные производные в этой точке равны нулю: 
, 
.
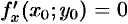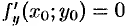Зафиксируем одну из переменных. Положим, например, 
. Тогда получим функцию 
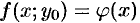одной переменной, которая имеет экстремум при 
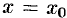. Следовательно, согласно необходимому условию экстремума функции одной переменной (см. п. 25.4), 
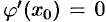, т.е. .
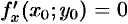Аналогично можно показать, что .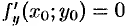
Геометрически равенства 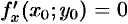и 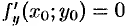означают, что в точке экстремума функции 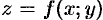касательная плоскость к поверхности, изображающей функцию 
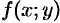, параллельна плоскости 
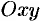, т. к. уравнение касательной плоскости есть 
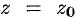(см. формулу (45.2)).
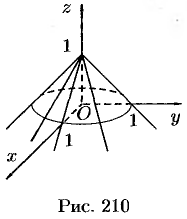
Замечание. Функция может иметь экстремум и точках, где хотя бы одна из частных производных не существует. Например, функция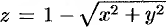 
имеет максимум в точке 
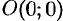(см. рис. 210), но не имеет в этой точке частных производных.
Точка, в которой частные производные первого порядка функции 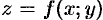равны нулю, т. е. 
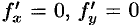, называется стационарной точкой функции 
.
Стационарные точки и ‘точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию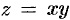 
. Для нее точка 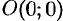является критической (в не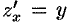й 
и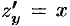 
обращаются в ноль). Однако экстремума в ней функция 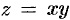не имеет, т. к. в достаточно малой окрестности точки 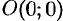найдутся точки для которых 
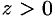(точки I и III четвертей) и 
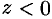(точки II и IV четвертей).
Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.
Теорема 46.2 (достаточное условие экстремума). Пусть в стационарной точке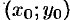 
и некоторой ее окрестности функция 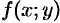имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 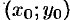значения 
, 
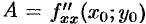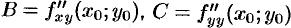. Обозначим
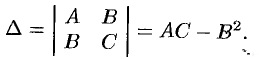
Тогда:
1) если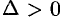 
, то функция в точке 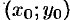имеет экстремум: максимум, если 
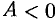; минимум, если 
;
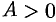2) если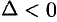 
, то функция 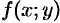в точке 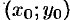экстремума не имеет.
В случае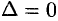 
экстремум в точке 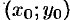может быть, может не быть. Необходимы дополнительные исследования.
Примем без доказательства.
Пример №46.1.
Найти экстремум функции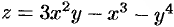 
.
Решение:
Здесь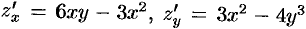 
. Точки, в которой частные производные не существуют, отсутствуют.
Найдем стационарные точки, решая систему уравнений:
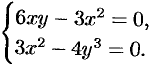
Отсюда получаем точк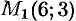и 
и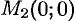 
.
Находим частные производные второго порядка данной функции:
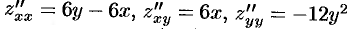
В точке 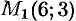имеем: 
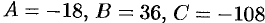, отсюда
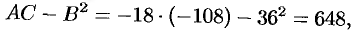
т.е. .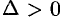
Так как 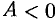, то в точке 
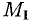функция имеет локальный максимум:
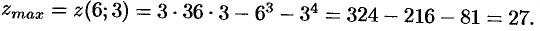
В точке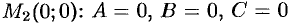 
и, значит, 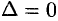. Проведем дополнительное исследование. Значение функции в точке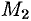 
равно нулю: 
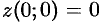. Можно заметить, что 
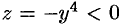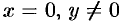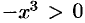при 
; 
при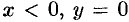 
. Значит, в окрестности точки 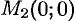функция принимает как отрицательные, так и положительные значения. Следовательно, в точке 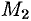функция экстремума не имеет.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дифференцирование неявной функции |
| Касательная плоскость и нормаль к поверхности |
| Наибольшее и наименьшее значения функции в замкнутой области |
| Задачи, приводящие к дифференциальным уравнениям |
